Вопрос 5

Осн. теоремы диф-го исчисления

Теорема Ролля

Пусть функция . Тогда Пусть x₁(a, b), тогда согласно теореме Ферма Данная теорема обладает таким же геометрическим истолкованием, что и теорема Ферма.

 Теорема Лагранжа

Пусть функция . Тогда Геометрическое истолкование теоремы Лагранжа. Строим график функции [a, b] (рис.10.2) ,  . Угловой коэффициент касательной в т.  . Следовательно, на графике функц .

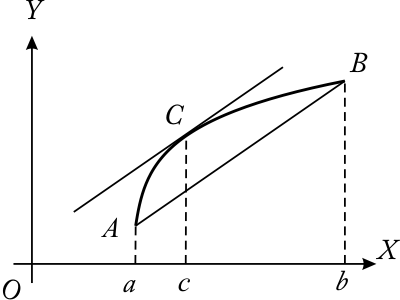Рис. 10.2

Теорема Коши

Пусть функции x(a, b). Тогда Существует c ­- хотя бы 1 (a, b). Теорема Коши является обобщением теоремы Лагранжа, где  .

 Теорема Ферма

Пусть функция  или f(c)=m в т. Пусть, для определённости, f(c)==M(рис. 10.1), тогда при и Согласно определению производной имеем

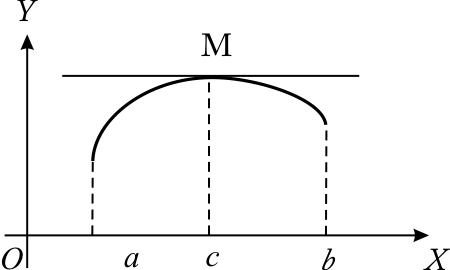Рис. 10.1 Геометрическое истолкование теоремы вытекает из геометрического смысла производной: касательная к графику функции y=f(x)в точке с абсциссой x=c параллельна оси OX.

Правила Лопиталя

Первое:

Расмотрим y=g(x) y=f(x), f(x₀)=0 g(x₀)=0

1. Существует lim_x→x0(f ’(x)/ g ’(x))=K=>

2. Существует

lim_x→x0(f (x)/ g (x))=K₁= lim_x→x0 (f ’(x)/ g ’(x))

3. Функции удовлетворяют условиям теоремы Коши

Пример:

lim_x→0(sin3x/x)=[0/0]= lim_x→0(3cos3x/1)=3

Замечание 1

lim_x→x0f (x)=0, lim_x→x0 g (x) =0 – Верно

дает дост. Условие существования lim_x→x0(f (x)/ g (x))

Достаточность – если теорема не выполняется, но рпедел есть.

Замечание 2

lim_x→x0(f (x)/ g (x)) = lim_x→x0 (f ’(x)/ g ’(x))= [0/0]= lim_x→x0 (f ’’(x)/ g ’’(x))=…=K

Второе:

lim_x→x0f (x)=∞, lim_x→x0 g (x) =∞ |

Существует f ’(x) g ’(x), в окрестностях x₀ | =>

lim_x→x0(f ’(x)/ g ’(x))=K₁ |

=> lim_x→x0(f (x)/ g (x))=K

Пример:

lim_x→∞((x+cos x)/x)=[∞/∞]= lim_x→∞((1-sin x)/1)=?????

Дополнение к правилам Лопиталя

Иногда их применяют несколько раз.

Существуют и другие неопределенности: [1^∞], [∞-∞], [0⁰], [∞⁰], [0*∞], но они должны быть приведены к основным с помощью преобразований функции под знаком предела.

Вопрос 6

Формула Тейлора

Задается функция y=f(x) которая в x₀ имеет все производные до n-го порядка f ‘(x₀),…, f ⁽ⁿ⁾ (x₀) – числа, причем f ⁽ⁿ⁺¹⁾ (x) – существует в окрестнсти x₀. f ‘(x₀),…, f ⁽ⁿ⁾ (x₀) – неприрывны в x₀ и окрестностях. Функция f(x) n раз в x₀ неприрывно диф-ма. При этих условиях ф-ю можно представить в виде (x₀=a)

R_n(x)= (f⁽ⁿ⁺¹⁾( Ѯ)/ n+1)*(x-a) ⁿ⁺¹

Ѯ=x₀+θ(x-a), 0<θ<1

Или F(x)=∑ ⁿ _k=0 (f ^k(x₀)/k!)* (x-a)^k+ R_n(x)

Применение:

Формула Тейлора позволяет вычислять значения функции с любой точьностью. Пусть известны значения f(a); f'(a); f"(a); f"'(a),...функции f(x) и её последовательный производных в начальной точке х=а. Требуется же найти значение функции при ином значении х. Вомногих случаях для этого достаточно вычислить значение многочлена Тейлора: f(a)+f'(a)/1!*(x-a)+f"(a)/2!*(x-a)^2+...+f(n)(a)/n!*(x-a)^n, взяв здесь два, три или большее число членов в зависимости от требуемой степени точности.

Осн. Разложения:

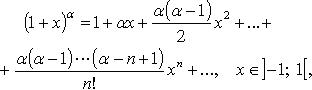
Оценка пограшности: (????????????????????????????)