19. Числовые характеристики непрерывных случайных величин

Распространим определения числовых характеристик дискретных величин на величины непрерывные. Начнем с математического ожидания.

Пусть непрерывная случайная величина X задана плотностью распределения f(x). Допустим, что все возможные значения X принадлежат отрезку [а, b]. Разобьем этот отрезок на п частичных отрезков длиной , ,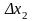..., 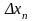и выберем в каждом из них произвольную точку x_i (i = 1, 2, ..., п). Нам надо определить математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений x_i на вероятности попадания их в интервал ; (напомним, что произведение f(х) приближенно равно вероятности попадания X в интервал ):

Перейдя к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный интеграл

Математическим ожиданием непрерывной случайной величины- X, Возможные значения которой принадлежат отрезку [a,b], называют определенный интеграл

M(X)= (*)

Если возможные значения принадлежат всей оси Ох, то

M(X)=

Предполагается, что несобственный интеграл сходится абсолютно, т. е. существует интеграл Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к — , а верхнего—к + .

По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения X принадлежат отрезку[a,b], то

D(X)=

если возможные значения принадлежат всей оси х, то

D(X)=

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

(X)= .

20 Нормальное распределение

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

Мы видим, что нормальное распределение определяется двумя параметрами: а и . Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков: а есть математическое ожидание, —среднее квадратическое отклонение нормального распределения.

а) По определению математического ожидания непрерывной случайной величины,

M(X)=

Введем новую переменную z = (x—а)/. Отсюда x=z+a, dx=dz. Приняв во внимание, что новые пределы интегрирования равны старым, получим

M(X)=

Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно a ( интеграл Пуассона ).

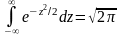Итак, М(Х) = а, т. е. математическое ожидание нормального распределения равно параметру а.

б) По определению дисперсии непрерывной случайной величины, учитывая, что М(Х) = а, имеем

D(X)=

Введем новую переменную z = (x—а)/. Отсюда х—a = z, dx = dz. Приняв во внимание, что новые пределы интегрирования равны старым, получим

D(X)=

Интегрируя по частям, положив u = z, dv= , найдем

D(X)=^

Следовательно,

(X)= .

Итак, среднее квадратическое отклонение нормального распределения равно параметру .

График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем функцию

y=

методами дифференциального исчисления.

1. Очевидно, функция определена на всей оси х.

2. При всех значениях х функция принимает положительные значения, т. е. нормальная кривая расположена над осью Ох.

3. Предел функции при неограниченном возрастании х (по абсолютной величине) равен нулю: , т. е. ось Ох служит горизонтальной асимптотой графика.

4.Исследуем функцию на экстремум. Найдем первую производную:

Легко видеть, что у' = 0 при х = а, у' > 0 при х < а, у' < 0 при х> а.

Следовательно, при х = а функция имеет максимум, равный

5.Разность х—а содержится в аналитическом выражении функции в

квадрате, т. е. график функции симметричен относительно прямой х= а.

6.Исследуем функцию на точки перегиба. Найдем вторую производную:

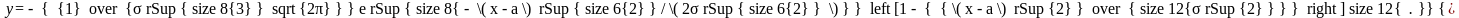
Легко видеть, что при х = а+ и х= а— вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции равно 1/( e)). Таким образом, точки графика (а—, 1/( e)) и (а + , 1/( e)) являются точками перегиба.

На рис. 7 изображена нормальная кривая при а=1, 2