16 Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X) = M[X — M(X)]²

Пусть случайная величина задана законом распределения

X	x1	x2	…	xn
p	p1	p2	…	pn

Тогда квадрат отклонения имеет следующий закон распределения:

[X-M(X)]2	[x1-M(X)]2	[x2-M(X)]2	…	[xn-M(X)]2
p	p1	p2	…	pn

По определению дисперсии,

D(X) = M [Х — М (X)]² = [x_i-M (X)]²p_l + [x₂-M (X)]² р₂ + ... +[х_п-М (Х)]²р_п.

Таким образом, для того чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания:

D (X) = М (X²) — [M (X)]².

Доказательство. Математическое ожидание М (X) есть постоянная величина, следовательно, 2М (X) и М² (X) есть также постоянные величины. Приняв это во внимание и пользуясь свойствами математического ожидания (постоянный множитель, можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), упростим формулу, выражающую определение дисперсии:

D (X) = М [Х — М (X)]² = М [Х²-2ХМ (X) + М² (Х)]=

= М (X²) — 2М (X) М (X) + М² (X) = М (X²) —2М² (X) + М² (X) =

М (X²)—M² (X).

Итак,

D(X)=M(X²)—[М(Х)]².

Квадратная скобка введена в запись формулы для удобства ее запоминания.

Свойство 1. Дисперсия постоянной величины С равна нулю:

D (С) = 0.

Доказательство. По определению дисперсии,

D(C)=M{[C-M(C)]²}.

Пользуясь первым свойством математического ожидания (математическое ожидание постоянной равно самой постоянной), получим

D (С) = М [(С—С)²] = М (0) = 0.

Итак,

D (С) = 0.

Свойство становится ясным, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяния, конечно, не имеет.

Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

D(CX)=C²D(X).

Доказательство. По определению дисперсии имеем

D (СХ) = М {[СХ — М (СХ)]²}.

Пользуясь вторым свойством математического ожидания (постоянный множитель можно выносить за знак математического ожидания), получим

D (СХ) = М {[СХ—СМ (X)]²} = М {С² [X — М (X)]²} =

= С² М {[Х — М (X)]²} = C²D (X).

Итак,

D(CX) = C²D(X).

Свойство становится ясным, если принять во внимание, что при | С | > 1 величина СХ имеет возможные значения (по абсолютной величине), большие, чем величина X. Отсюда следует, что эти значения рассеяны вокруг математического ожидания М (СХ) больше, чем возможные значения X вокруг М(Х), т. е. D(CX)>D(X). Напротив, если 0 < | С | < 1, то D (СХ) < D (X).

Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

D(X + Y) = D(X) + D(Y).

Доказательство. По формуле для вычисления дисперсии имеем

D (X + Y) = М [(X + Y)²] — [М (X +Y)]².

Раскрыв скобки и пользуясь свойствами математического ожидания суммы нескольких величин и произведения двух независимых случайных величин, получим

D (X + Y) = М [X² + 2ХY + Y²] — [M (X) + М (Y)]² =

= М (X²) + 2М (X) • М (Y) + М (Y²) — М² (X) — 2М (X) • М (Y) — M² (Y) = {М (X²) — [М (X)]²} +{M(Y²)-[M(Y)]²}=D(X)+D(Y).

Итак,

D (X + Y) = D(X)+D(Y).

Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.

Например, для трех слагаемых имеем

D(X+Y+Z)=D[X+(Y+Z)] =D(X)+D(Y+Z)=D(X)+D(Y)+D(Z).

Для произвольного числа слагаемых доказательство проводится методом математической индукции.

Следствие 2. Дисперсия суммы постоянной величины и случайной равна дисперсии случайной величины:

D(C+X)=D(X).

Доказательство. Величины С и X независимы, поэтому, по третьему свойству,

D(C+X)=D(C)+D(X).

В силу первого свойства D (С) = 0. Следовательно,

D(C+X)=D(X).

Свойство становится понятным, если учесть, что величины X и X+С отличаются лишь началом отсчета и, значит, рассеяны вокруг своих математических ожиданий одинаково.

Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

D(X-Y)=D(X)+D(Y).

Доказательство. В силу третьего свойства

D(X-Y)=D(X)+D(-Y).

По второму свойству,

D(X—Y) = D(X)+(-1²)D(Y),

или

D(X — Y) = D(X)+D(Y).

17 Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, т. е.

F(x)=P(X < х).

Геометрически это равенство можно истолковать так: F (х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Свойства функции распределения

Свойство 1. Значения функции распределения принадлежат отрезку [О, 1]:

0 F (х) 1.

Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.

Свойство 2. F (х)—неубывающая функция, т. е.

F (x₂) F (х₁), если х₂ > х₁.

Доказательство. Пусть х₂ > х₁. Событие, состоящее в том, что X примет значение, меньшее х₂, можно подразделить на следующие два несовместных события: 1) X примет значение, меньшее х₁, с вероятностью Р (X < x₁); 2) X примет значение, удовлетворяющее неравенству x₁ X x₂, с вероятностью Р (x₁ X x₂). По теореме сложения имеем

Р (X < х₂) = Р (X < х₁) + Р (x₁ X x₂).

Отсюда

Р (X < х₂) - Р (X < х₁)= Р (x₁ X x₂),

или

F (x₂)—F (x₁) = Р (x₁ X x₂). (*)

Так как любая вероятность есть число неотрицательное, то F(x₂) — F(x₁) 0, или F (x₂) F (x₁), что и требовалось доказать.

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:

P(a X<b)=F(b)—F(a). (**)

Это важное следствие вытекает из формулы (*), если положить х₂=b и х₁= а.

Пример. Случайная величина X задана функцией распределения

Найти вероятность того, что в результате испытания X примет знамение, принадлежащее интервалу (0, 2):

Р (0 X 2)=F(2)-F(0).

Решение. Так как на интервале (0, 2), по условию,

F(x) = x/4+1/4,

то

F (2) — F (0) = (2/4+ 1/4)- (0/4+ 1/4) = 1/2.

Игак,

Р(0 < X < 2) = 1/2.

Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Действительно, положив в формуле (**) а = х₁, b = х₁+ , имеем

P(х₁ X<х₁+ )=F(х₁+ )-F(х₁).

Устремим к нулю. Так как X — непрерывная случайная величина, то функция F (х) непрерывна. В силу непрерывности F (х) в точке х₁ разность F (х₁+ )— F (x₁) также стремится к нулю; следовательно, Р (X =х₁) = 0. Используя это положение, легко убедиться в справедливости равенств

Р (а X < b) = Р (а < X < b) = Р(а<Х b) = Р(а Х b). (***)

Например, равенство Р(а<Х b) = Р (а < X < b) доказывается так:

Р(а<Х b) = Р (а < X < b)+P(X=b)= Р(а<Х<b).

Таким образом, не представляет интереса говорить о вероятности того, что непрерывная случайная величина примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый. Этот факт полностью соответствует требованиям практических задач. Например, интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их совпадения с проектным размером.

Заметим, что было бы неправильным думать, что равенство нулю вероятности Р (X =х₁) означает, что событие Х=х₁ невозможно (если, конечно, не ограничиваться классическим определением вероятности). Действительно, в результате испытания случайная величина обязательно примет одно из возможных значений; в частности, это значение может оказаться равным х₁.

Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F(x) = 0 при х а; 2) F(x)=1 при х b.

Доказательство. 1) Пусть x₁ a. Тогда событие X < х₁ невозможно (так как значений, меньших х₁, величина X по условию не принимает) и, следовательно, вероятность его равна нулю.

2) Пусть х₂ b. Тогда событие X < х₂ достоверно (так как все возможные значения X меньше х₂) и, следовательно, вероятность его равна единице.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:

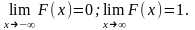
Замечание. График функции распределения дискретной случайной величины имеет ступенчатый вид. Убедимся в этом на примере.

Пример. Дискретная случайная величина X задана таблицей распределения

X	1	4	8
p	0,3	0,1	0,6

Найти функцию распределения и вычертить ее график.

Решение. Если х 1, то F(x)=0 (третье свойство). Если 1 < х 4, то F(х)=0,3. Действительно, X может принять значение 1 с вероятностью 0,3.

Если 4 < х 8, то F (х)=0,4. Действительно, если х₁ удовлетворяет неравенству 4 < x₁ 8, то F (x₁) равно вероятности события X < х₁, которое может быть осуществлено, когда X примет значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность этого события равна 0,1). Поскольку эти два события несовместны, то по теореме сложения вероятность события X < х₁ равна сумме вероятностей 0,3 + 0,1=0,4.

Если х > 8, то F(x) = 1. Действительно, событие Х 8 достоверно, следовательно, его вероятность равна единице.

Итак, функция распределения аналитически может быть записана так:

График этой функции приведен на рис. 3.

18 Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f (х)— первую производную от функции распределения F (х):

f (х) = F' (х).

Из этого определения следует, что функция распределения является первообразной для плотности распределения.

Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.

Нахождение функции распределения по известной плотности распределения

Зная плотность распределения f(х), можно найти функцию распределения F (х) по формуле

F(x) =

Действительно, мы обозначили через F (х) вероятность того, что случайная величина примет значение, меньшее х, т. е.

F(x) = P(X<x).

Очевидно, неравенство X < х можно записать в виде двойного неравенства - < X < х, следовательно,

F(х)=Р(- < X < х) (*)

Полагая в формуле (*) (см. § 2) а=- , b = х, имеем

Р(- < X < х) =

Наконец, заменив Р (- < X < х) на F (х), в силу (*), окончательно получим

F(x) =

Таким образом, зная плотность распределения, можно найти функцию распределения. Разумеется, по известной функции распределения может

быть найдена плотность распределения, а именно:

f(x)=Г’(x).

Свойство 1. Плотность распределения—неотрицательная функция:

f(x) 0.

График плотности распределения называют кривой распределения.

Свойство 2. Несобственный интеграл от плотности распределения в пределах от - до равен единице: