14 Биномиальное распределение

Биномиальное распределение. Дискретная случайная величина Х имеет биномиальное распределение, если ее возможные значения 0, 1, 2, ... , m, … , n,  а соответствующие им вероятности равны:

P(X= k) = , где  k=0,1,…n                (21)

где  0 < p < 1,  q = 1 – p ;  m = 0, 1, 2, ... , n.  

Как видно из (21), вероятности Рm вычисляются, как члены разложения бинома Ньютона , откуда и название «биномиальное распределение».

Примером является выборочный контроль качества производственных изделий, при котором отбор изделий для пробы производится по схеме случайной повторной выборки, т.е. когда проверенные изделия возвращаются в исходную партию. Тогда количество нестандартных изделий среди отобранных есть случайная величина с биномиальным законом распределения вероятностей.

Биномиальное распределение определяется двумя параметрами: n  и  p. Cлучайная величина, распределенная по биномиальному закону, имеет следующие основные числовые характеристики: M(X)=np.

дисперсия каждой из остальных случайных величин равна pq

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии  

Пример. Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины X — числа выпадений «герба».

Решение. Вероятность появления «герба» в каждом бросании монеты р=1/2, следовательно, вероятность непоявления «герба» q= 1 — 1/2=1/2.

При двух бросаниях монеты «герб» может появиться либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения X таковы: x₁ = 2, x₂==1, x₃ = 0. Найдем вероятности этих возможных значений по формуле Бернулли:

Р₂ (2) = 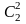p² = (1 /2)² = 0,25,

Р₂ (1) = pq=2*(1/2)*(1/2)=0,5,

Р₂ (0) = q² = (1 /2)² = 0,25.

Напишем искомый закон распределения:

X	2	1	0
p	0,25	0,5	0,25

Контроль: 0,25 + 0,5 + 0,25=1.

15 Математическое ожидание дискретной случайной величины

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина X может принимать только значения х₁, х₂, ..., х_п, вероятности которых соответственно равны р_1, р₂, . . ., р_п. Тогда математическое ожидание М (X) случайной величины X определяется равенством

М (X) = х₁р₁ + х₂р₂ + … + x_np_n.

Если дискретная случайная величина X принимает счетное множество возможных значений, то

М(Х)=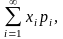

причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:

М (С) = С.

Доказательство. Будем рассматривать постоянную С как дискретную случайную величину, которая имеет одно возможное значение С и принимает его с вероятностью р = 1. Следовательно,

М (С) = С*1= С.

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:

Доказательство. Пусть случайная величина X задана законом распределения вероятностей:

X	x1	x2	…	xn
p	p1	p2	…	pn

Учитывая замечание1, напишем закон распределения случайной величины CX:

CX	Cx1	Cx2	…	Cxn
p	P1	P2	…	pn

Математическое ожидание случайной величины СХ:

M(CX) = Cx₁p₁ + Cx₂p₂+...+Cx_np_n = С (х₁р₁ + x₂p_z + . .. + х_пр_п) = СМ (X).

Итак,

М(СХ)=СМ(Х).

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

M(XY) = M(X)M(Y).

Доказательство. Пусть независимые случайные величины X и Y заданы своими законами распределения вероятностей (Для упрощения выкладок мы ограничимся малым числом возможных значений. В общем случае доказательство аналогичное):

X	x1x2	Y	y1y2
P	p1p2	g	g1g2

Составим все значения, которые может принимать случайная величина XY. Для этого перемножим все возможные значения X на каждое возможное значение Y; в итоге получим х₁у₁, х₂у₁, х₁у₂ и х₂у₂. Учитывая замечание 3, напишем закон распределения XY, предполагая для простоты, что все возможные значения произведения различны (если это не так, то доказательство проводится аналогично):

XY	х1у1	х2у1	х1у2	х2у2
p	p1g1	p2g1	p1g2	p2g2

Математическое ожидание равно сумме произведений всех возможных значений на их вероятности:

М (XY) = х₁у₁* p₁ g₁+ х₂у₁* p₂ g₁+ х₁у₂* p₁ g₂+ х₂у₂* p₂ g₂

или

М (XY) = y₁g₁ (х₁р₁ + x₂ p₂) + y₂g₂ (x₁ p₁+ x₂p₂)=( x₁ p₁+ x₂ p₂)( y₁g₁+ y₂g₂) = M(X)*M(Y)

Итак, M(XY) = M(X)*M(Y).

Следствие. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий.

Например, для трех случайных величин имеем:

М (XYZ) = М (XY*Z) = M (XY) M(Z) = M (X) М (Y) M `.

Для произвольного числа случайных величин доказательство проводится методом математической индукции.

Следующее ниже свойство справедливо как для независимых, так и для зависимых случайных величин.

Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

М (X + Y) = М (X) + М (Y).

Доказательство. Пусть случайные величины X и Y заданы следующими законами распределения (Чтобы упростить вывод, мы ограничились лишь двумя возможными значениями каждой из величин. В общем случае доказательство аналогичное):

X	x1	x2	Y	y1	y2
P	p1	p2	g	g1	g2

Составим все возможные значения величины Х + Y. Для этого к каждому возможному значению X прибавим каждое возможное значение Y; получим х₁+у₁, х₁ + у₂, х₂+у₁, х₂ + у₂, Предположим для простоты, что эти возможные значения различны (если это не так, то доказательство проводится аналогично), и обозначим их вероятности соответственно через р₁₁, р₁₂, р₂₁ и р₂₂.

Математическое ожидание величины Х + Y равно сумме произведений возможных значений на их вероятности:

M(X+Y)=( х₁+у₁) р₁₁+( х₁ + у₂) р₁₂+( х₂+у₁) р₂₁+( х₂ + у₂) р₂₂,

или

M(X + Y)=x₁ (р₁₁ + р₁₂) + х₂ (р₂₁ + р₂₂) + у₁ (р₁₁ + р₂₁)+ у₂ (р₁₂+ р₂₂ ). (*)

Докажем, что р₁₁ + р₁₂= p₁. Событие, состоящее в том, что X примет значение х₁ (вероятность этого события равна р₁), влечет за собой событие, которое состоит в том, что X+Y примет значение x₁+y₁ или х₂+ у₂ (вероятность этого события по теореме сложения равна р₁₁ + р₁₂) и обратно. Отсюда и следует, что р₁₁ + р₁₂= p₁. Аналогично доказываются равенства

р₂₁ + р₂₂=p₂ , р₁₁ + р₂₁=g₁ и р₁₂+ р₂₂=g₂.

Подставляя правые части этих равенств в соотношение (*), получим

M(X+Y)=(x₁p₁+ х₂р₂) +(y₁g₁+y₂g₂),

или окончательно

М (X + Y) = М (X) + М (Y).

Следствие. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых.

Например, для трех слагаемых величин имеем

M(X+Y+Z)=M[(X+Y)+Z]= М (X + Y)+ M (Z) = М (X) + М (Y) + М (Z).

Для произвольного числа слагаемых величин доказательство проводится методом математической индукции.