10.Метод интегрирования по частям. Примеры.

Пусть ф-я u и v, а также их произв-е явл-ся дифференц-ми ф-ми, тогда .

Пусть u = u(x), v = v(x) – дифференцируемы на D

d(u•v) = du•v + u•dv  ∫ d(u•v) = ∫du•v + ∫u•dv  u•v = ∫v•du + ∫u•dv 

∫u•dv = u•v - ∫v•du – формула интегрирования по частям

Применение данной формулы:

1. P_n (x)•φ(x)dx; P_n (x) – многочлен n-ой степени

а ) φ(x) = sin ax u = P_n (x); dv = φ(x)dx

cos ax

e^Kx

b ) φ(x) = обратные тригонометрические функции u = φ(x); dv = P_n (x)dx

log_ax

2 . e^kx•sin ax dx в этом случае любой из множителей можно принять

e^kx•cos ax dx за u

11.Двукратное интегрирование по частям на примере Найти неопределенный интеграл

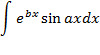
Дважды интегрируем по частям и сводим интеграл к себе:

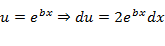
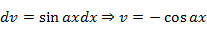
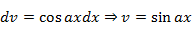
В результате двукратного интегрирования по частям интеграл свёлся к самому себе. Приравниваем начало и концовку решения:

Переносим   в левую часть со сменой знака и выражаем наш интеграл:

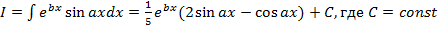
Теперь вернемся к началу примера, а точнее – к интегрированию по частям:

За   мы обозначили экспоненту.

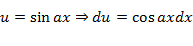
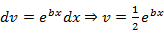
за   можно обозначить и тригонометрическую функцию. Но, в рассмотренном примере это менее рационально, поскольку появятся дроби.

12.Интегралы от функций, содержащих квадратный трехчлен . Примеры.

1. Интегрирование выражений, сод-х квадратный трехчлен

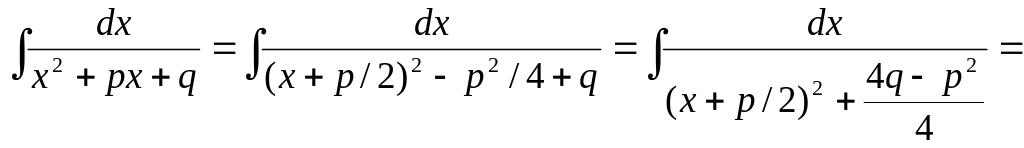x +p/2=t dx=dt a²= или

_IV

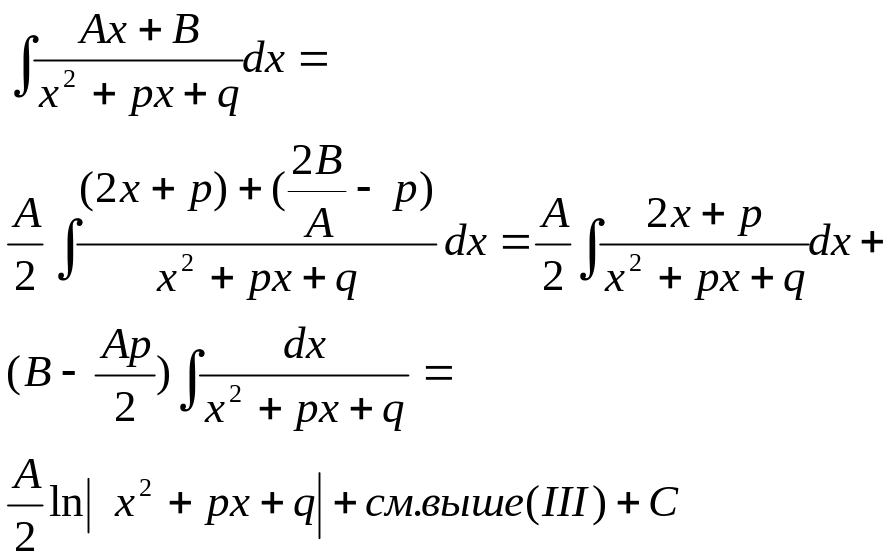
V. p²/4-q>0

p²/4-q<0

13. Интегралы от ф-ий, содер-их квадратный трёхчлен.

Инт-лы вида можно свести к табличн. путём выделения полного квадрата в квадратн. трёхчлене. = = .Для нахожд-я инт. вида в числит. выделяют производную квадратного трёхчлена, стоящего под знаком корня, затем раскладываю инт-л на сумму 2-х инт-ов, один их к-х табл-й, а др. вида . .

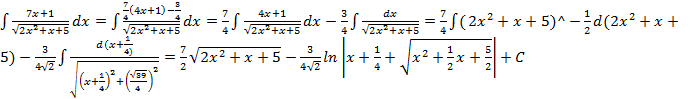14.Интегрирование рациональных дробей с помощью разложения их на простейшие дроби. Примеры.

1. Многочленом степени n наз-ся выражение вида a₀+a₁x+a₂x²+…+a_nxⁿ=P_n(x)

Рациональной дробью наз-ют отношение двух многочленов вида При n=0 вычисление интеграла никаких трудностей не представляет

Интерес представляют рациональные дроби, у кот. n>0 При этом будем рассматривать дроби, у кот. m<n Если m>=n, то применяют процедуру деления многочленов уголком

2. Интегрирование простейших дробей

I . x-a=t dx=dt

I I. x-a=t dx=dt

15. Интегрирование тригонометрических функций.

∫ cosax sinbxdx, ∫ cosax cosbxdx , ∫ sinax sinbxdx.

где a ≠b, находятся с помощью формул:

sinax cosbx= 1/2(sin(a-b)x+sin(a+ b)x),

Cos ax cos bx = 1/2(cos(a- b)x+ cos(a+b)x ),

Sinax sin bx=1/2(cos(a -b)x- cos(a+b)x).

Пример. Найти ∫ sin 2x sin 4xdx. Решение. ∫sin2xsin4xdx=∫1/2(cos(2x-4x) –cos(2x+4x))dx =1/2 ∫ cos2xdx-1/2∫ cos6xdx=1/2 − 1/2 +C= 1/4sin2x- 1/12sin6x+c.

Вычисление интегралов вида: ∫ R (sinx,cosx)dx , где − R рациональная функция. Если выполнено:

R(-sinx, cosx) =-R (sinx cosx) , то подстановка t = cos x;

R(sinx,- cosx) =-R (sinx, cosx) , то подстановка t = sin x;

R(-sinx, -cosx) =R (sinx cosx) , то подстановка t = tg x;

Пример. Найти ∫ cos³xdx. Решение. Пусть t= sin x, dt= cos³xdx, cos²x=1- sin²x.

Тогда ∫ cos ³xdx=∫ cos ²x cos xdx= ∫(1-t²)dt=∫1⋅dt − ⋅ ∫t²dt = t- + C= sinx- + C

Если ни одно из вышеуказанных равенств не выполняется, то

целесообразно применять так называемую универсальную

тригонометрическую подстановку: t =tg x/2 , sinx= (2tg x/2):(1+tg²x/2)=2t:(1+y²), cos x=(1-tg²x/2):(1+tg²x/2)=(1-t²):(1+t²), x = 2 arctg t, dx= 2dt/(1+ t²)