1.4.4 Перевод чисел из шестнадцатеричной системы счисления в двоичную
Чтобы перевести число из шестнадцатеричной системы счисления в двоичную, необходимо каждую цифру шестнадцатеричного числа заменить двоичной тетрадой из таблицы.
(16,599)16 – (10110,010110011001)2
1.4.5 Перевод чисел из двоичной системы счисления в шестнадцатеричную
Чтобы перевести число из двоичной системы счисления в шестнадцатеричную систему счисления, необходимо, двигаясь вправо и влево от запятой, разбить двоичное число на тетрады. Крайние тетрады в случае необходимости добавляются нулями.
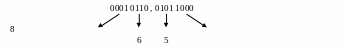
(10110,01011000)2 – (16,58)16
1.5 Прямой, обратный, дополнительный коды
Мы будем изучать эти коды, т.к. в ЭВМ нет операции вычитания, и она заменяется операцией сложения с обратным кодом.
Прямым кодом целого двоичного числа Х будет называться число, образованное по формуле:
Прямым кодом дробного двоичного числа X будет называться число, образованное по формуле:
Обратным кодом целого двоичного числа X называется число, образованное по формуле:
О
Правило: Чтобы получить обратный код двоичного целого числа, в знаковый разряд нужно поставить 1, а значащие разряды проинвертировать (0 заменить 1,а 1 заменить 0).
0
. 101
Знаковый разряд Значащие разряды
1 . 101
A = 0.0100 +4 прямой код;
А = 1.1011 -4 обратный код;
Для положительных чисел прямой и обратный коды совпадают.
Правило алгебраического суммирования: Чтобы произвести суммирование (алгебраическое) двоичных кодов чисел с использованием обратных кодов, необходимо все положительные числа представить в прямом коде, а отрицательные - в обратном, и просуммировать коды чисел, включая знаковые разряды.
Если возникает единица переноса из знакового разряда, то она прибавляется к младшему разряду.
Если в знаковом разряде получается 0, то это означает, что результат положительный и представлен в прямом коде.
Если в знаковом разряде результата 1, то это означает, что результат отрицательный и представлен в обратном коде.
Для получения прямого кода необходимо в знаковом разряде оставить 1, а значащие разряды проинвертировать (по правилу полинома можно переводить в десятичную систему счисления только прямой код числа).
Пример:
А=5, В=4
0.0101 +5 прямой код 0.0100 +4 прямой код
1.1010 -5 обратный код 1.1011 -4 обратный код
А+В
+
0.0100 +4 прямой код
0.1001
+9 прямой код
А-В
+
1.1011 -4 обратный код
1 0.0000
+1
0.0001 прямой код
Знаковый разряд результата равен 0. Из этого следует, что результат положительный и представлен в прямом коде.
В-А
+
1.1010 -5 обратный код
1.1110
Знаковый разряд результата равен 1. Следовательно, результат получился отрицательным и представлен в обратном коде. Прямой код результата равен:
1.0001 прямой код
Дополнительным кодом целого двоичного числа называется число, образованное по формуле:
Дополнительным кодом дробного двоичного числа называется число, образованное по формуле:
Правило: Чтобы получить дополнительный код двоичного отрицательного числа необходимо в знаковый разряд поставить 1, все значащие разряды проинвертировать и к младшему разряду прибавить 1.
Это применимо как для целых так и для дробных чисел.
Пример:
А
=5,
В=4
1
+
+
1 1
1
.1011
-5 дополнительный код
1.1100 -4 дополнительный код
Для положительных чисел прямой и дополнительный коды совпадают.
Правило: Чтобы выполнить алгебраическое суммирование двоичных чисел с использованием дополнительного кода, положительные числа представляются в прямом коде, отрицательные – в дополнительном, и производится суммирование кодов чисел, включая знаковые разряды.
Если возникает единица переноса из знакового разряда, то она отбрасывается.
Если в знаковом разряде 1, значит результат отрицательный и представлен в дополнительном коде.
Чтобы получить прямой код результата, необходимо в знаковом разряде оставить 1, значащие разряды проинвертировать, к младшему разряду прибавить 1.
Пример:
А-В
+
0.0101 +5 прямой код
0.0001
+1 прямой
код
1
Если образовался “0” в знаковом разряде, то число получилось положительным и представлено в прямом коде, а если “1”, то это число отрицательное и представлено в дополнительном коде.
Пример:
В-А
+
1.1011 -5 дополнительный код
1.1111
Знаковый разряд результата равен 1. Из этого следует, что результат получился отрицательным и представлен в дополнительном коде. Прямой код результата равен:
+
1
1.0001 -1 прямой код