1

ТЕОРИЯ КРИВЫХ

Наглядно кривую можно представить как след точки, движущейся по плоскости или в пространстве.

Кажется совсем несложным дать этому наглядному представлению простое математическое описание, например определить кривую как непрерывный образ отрезка.

Однако существуют примеры, подвергающие такой подход серьезному испытанию: непрерывный образ отрезка может заполнять, в частности, целый квадрат.

Для определения кривой мы изберем следующий путь.

Сначала введем понятие простой кривой, затем более общее понятие кривой, заданной параметрически.

Чтобы привлечь к изучению свойств введенного класса кривых аппарат дифференциального исчисления, накладываем на кривые ряд дополнительных ограничений геометрического характера.

Полученный класс гладких кривых будет обладать свойствами, хорошо согласующимися с наглядными представлениями.

Дальнейшие ограничения приводят нас к регулярным кривым.

Для этих кривых определяются такие важные скалярные характеристики кривой, как кривизна и кручение.

Привлекая их к изучению локального строения кривых, мы получаем целый ряд полезных фактов и соотношений.

§ 1. Понятие кривой

1. Простая плоская кривая

Пусть функции (t) и (t) аргумента (параметра) t непрерывны на сегменте [а, b].

Рассмотрим множество L точек М(х, у), координаты х и у которых определяются соотношениями (рис. 1)

x=(t), y=(t), a≤t≤b. (1)

Множество L будем называть простой плоской кривой, если различным значениям параметра t из сегмента [a, b] отвечают различные точки этого множества.

Будем говорить также: «соотношения (1) определяют простую плоскую кривую L» и «простая плоская кривая L параметризована при помощи соотношений (1)».

Если считать параметр t физической величиной — временем, то простую плоскую кривую можно представлять как траекторию движущейся по плоскости точки, причем эта траектория не имеет точек самопересечения и участков самоналегания.

Точки М(х, у), координаты которых определяются соотношениями (1), назовем точками кривой L.

Точки А и В, отвечающие граничным значениям а и b параметра t, назовем граничными точками кривой L.

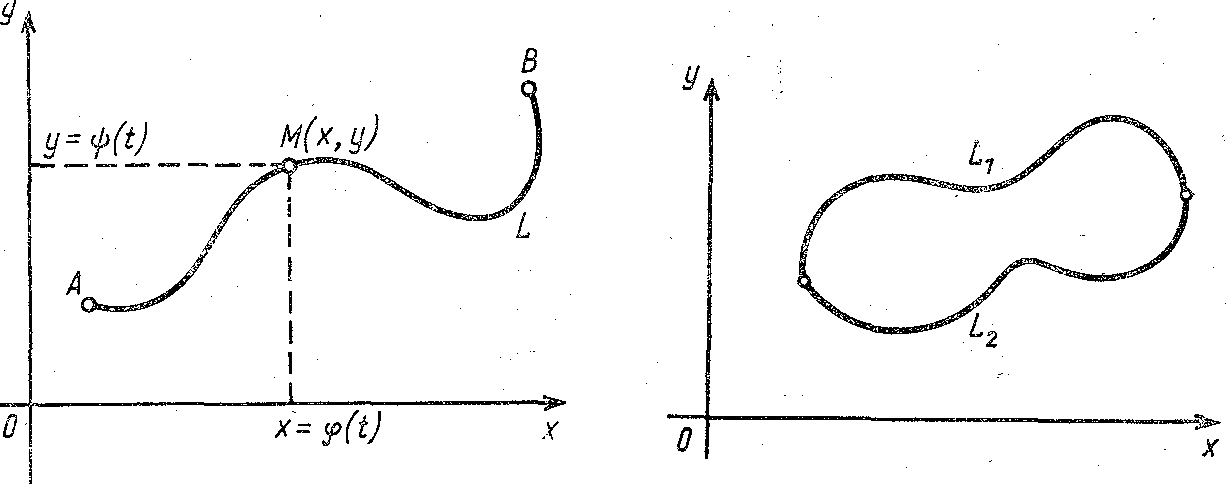
Рис. 1. Точка М(х, у) движется по кривой L от точки А до точки В по закону (1)

Рис. 2. Простая замкнутая кривая L — объединение простых кривых L1 и L2

Примером простой плоской кривой может служить график непрерывной на сегменте [а,b] функции y=f(x).

Этот график есть множество точек М, координаты х и у которых определяются соотношениями x=t, y=f(t), a≤t≤b.

Ясно, что различным значениям параметра t отвечают различные точки графика.

Замечание 1. Одна и та же простая кривая может быть параметризована различными способами. Можно, например, рассматривать параметризацию простой кривой L, получающуюся из данной ее параметризации x=(t), y=(t), a≤t≤b, путем представления параметра t в виде непрерывной строго монотонной функции другого параметра s:

x=(t(s)), y=(t(s)), a₁≤s≤b₁

Замечание 2. Важным является понятие простой замкнутой плоской кривой.

Пусть L₁ и L₂ — две простые плоские кривые, такие, что:

1. каждая из граничных точек кривой L₁, совпадает с одной из граничных точек кривой L₂;

2. любые неграничные точки кривых L₁ и L₂ различны.

Множество L, полученное объединением кривых L₁ и L₂, называется простой замкнутой плоской кривой.

Простая замкнутая плоская кривая также может быть параметризована при помощи соотношений вида (1) (рис. 2).

2. Плоские кривые, задаваемые параметрически

Истоком такого способа задания кривых служит представление о кривой как о совокупности последовательных положений движущейся точки.

Обратимся к примеру.

Пример 1. Совокупность последовательных положений точки М(х, у), движущейся по плоскости при изменении параметра t от −∞ до +∞ по закону

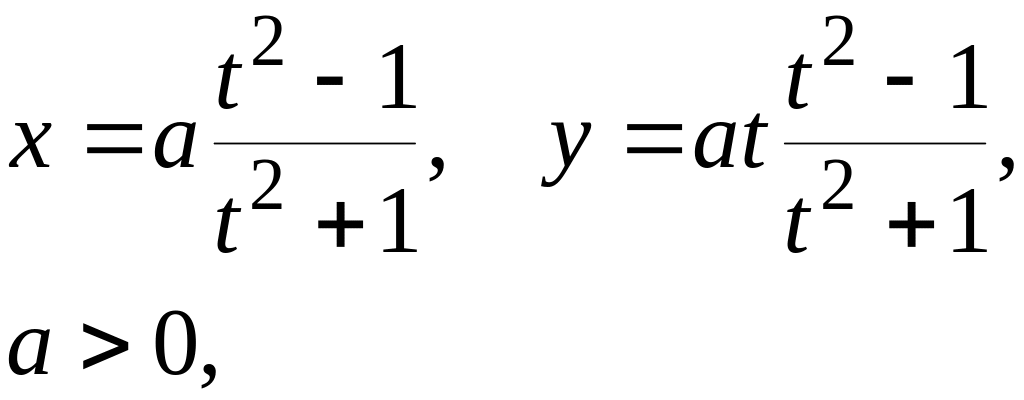
п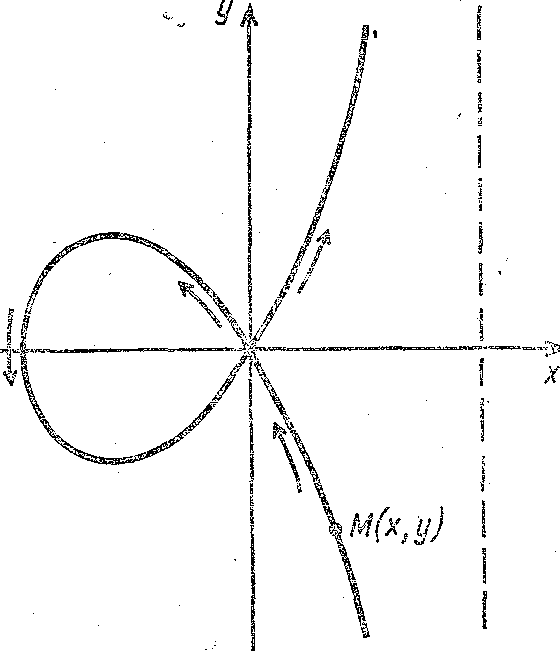 редставляет собой кривую, называемую строфоидой.

Рис. 3. Строфоида: указан порядок прохождения кривой при изменении параметра t от−∞ до +∞

Заметим, что при изменении параметра t в указанных пределах движущаяся по строфоиде точка М(х, у) попадает в начало координат О(0, 0) дважды: при t=−1 и при t=+1.

Так как мы рассматриваем здесь последовательные положения движущейся точки, то точки строфоиды, отвечающие этим различным значениям параметра t, считаются различными: каждая точка на строфоиде как бы помечается отвечающим этой точке значением параметра t (рис. 3).

Строфоиду можно представить как объединение простых плоских кривых.

В самом деле, разобьем область изменения параметра t, т. е. числовую прямую R, на частичные сегменты [п, п+1], п=0, ±1, ±2,…

Когда параметр t изменяется на каждом таком сегменте, то соответствующая часть строфоиды — простая кривая.

Ясно, что объединение всех таких частей представляет собой всю строфоиду (рис. 4).

Перейдем теперь к определению кривой, задаваемой параметрически.

Будем считать, что область {t} изменения параметра t — связное множество на прямой:

1. сегмент;

2. полусегмент (полуинтервал) или замкнутая полупрямая;

3. интервал, открытая полупрямая или вся прямая.

Под разбиением D области {t} изменения параметра t на частичные сегменты будем понимать следующую процедуру.

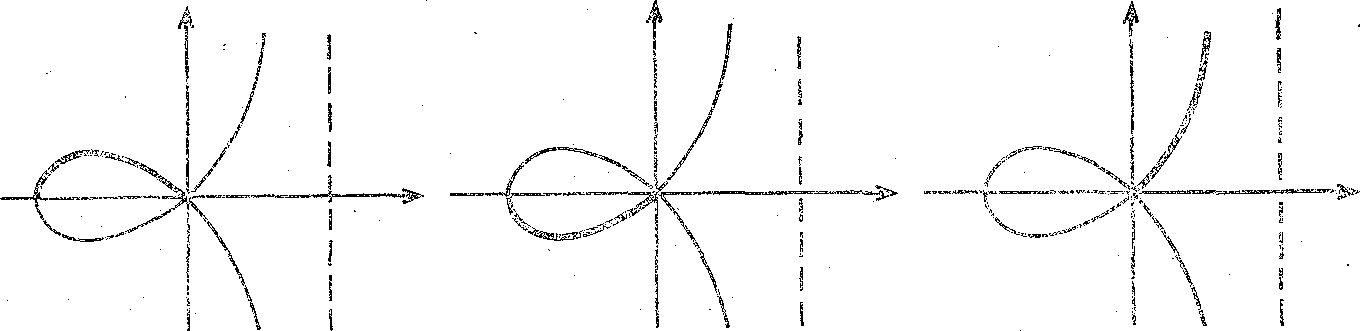
t[-1,0] t[0,1] t[1,2]

Рис. 4. Простые участки прямой строфоиды

В случае 1)

• сегмент [а,b] разбивается на частичные сегменты [t_i, t_i+1] при помощи конечного числа точек a=t₀<t₁<t₂<...<t_n=b.

В случае 2)

• полусегмент [а, b) или полупрямая [а,+∞) разбивается на частичные сегменты [t_i, t_i+1] при помощи точек a=t₀<t₁<t₂<…<t_n,

• причем t_n b для полусегмента [а,b)

• и t_n+∞ для полупрямой [а,+∞);

• для полусегмента (а, b] и полупрямой (−∞,b] разбиение производится при помощи точек …t_-n<...<t_-2<t_-1<t₀=b,

• причем t_-nа для полусегмента

• и t_-n−∞ для полупрямой при n∞.

В случае 3)

• разбиение интервала (а,b), открытой полупрямой (а,+∞) или всей прямой (−∞,+∞) на частичные сегменты [t_t,t_i+1] строится при помощи точек ...t_-n<...<t_-2<t_-1<t₀<t₁<t₂<…<t_n,...,

• причем t_-nа, t_nb для интервала (a, b),

• t_-na, t_n+∞ для полупрямой (a, +∞),

• t_-n−∞, t_n+∞ для прямой (−∞,+∞);

• для полупрямой (−∞, b) t_-n−∞, t_nb, при n∞

Пусть функции (t) и (t) параметра t непрерывны на связном множестве {t}.

Будем говорить, что соотношения

x=(t), y= (t), t{t}, (2)

представляют собой параметрические уравнения плоской кривой L, если существует такое разбиение области {t} на частичные сегменты [t_i, t_i+1], что при изменении параметра i на каждом таком сегменте соотношения (2) определяют простую плоскую кривую.

Сама кривая L и есть объединение всех указанных простых кривых (с учетом их возможных самопересечений и самоналеганий) при условии монотонного изменения параметра t по множеству {t}.

При этом говорят, что кривая L задана параметрически при помощи соотношений (2).

Пример 2. Соотношения

x=e^-tcos t, у=0, 0<t<+∞, (3)

представляют собой параметрически заданную кривую.

Чтобы убедиться в этом, рассмотрим следующее разбиение области {t}=[0, +∞) на частичные сегменты: [t_i, t_i+1], i=0, 1, 2, ..., где t_i= i.

Если t изменяется на таком сегменте, то соотношения (3) определяют простую кривую — сегмент оси Ох с граничными точками e^{- i} cos i и e^{- (i+1)}cos(i+1).

Кривая L, определяемая параметрическими уравнениями (3), — это траектория точки, совершающей затухающие колебания на оси Ох с амплитудами 1, е^-, е^-2, ... (рис. 5).

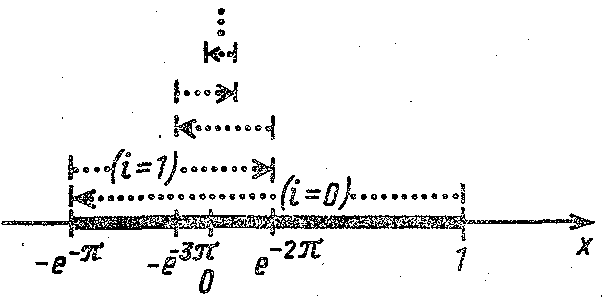
Рис. 5. Схематическое изображение кривой, имеющей бесконечное число участков самоналегания

Пример 3. Рассмотрим кривую L, заданную параметрически при помощи соотношений

x=cos(t), y=sin(t), 0≤t≤4. (4)

Система сегментов [0,], [, 2], [2, 3], [3, 4] разбивает множество М=[0, 4].

Для значений t из каждого сегмента этой системы соотношения (4) определяют простую кривую (полуокружность).

Ясно, что L — окружность, дважды обходимая против часовой стрелки.