2.2. Аналоговые методы модуляции

Модуляцией называется процесс, в результате которого происходит изменение параметра или параметров сигнала-переносчика пропорционально другому сигналу, сигналу сообщения. При аналоговой модуляции модулированный сигнал аналитически может быть представлен в комплексной форме:

, (2.56)

где A(t) – изменяющаяся во времени амплитуда (огибающая), ₀ – частота несущей, (t) – изменяющаяся во времени фаза.

Для узкополосных сигналов, удовлетворяющих условию W << ₀ (W – ширина спектра), параметры A(t) и (t) изменяются достаточно медленно по сравнению с ехр(j₀t).

АМПЛИТУДНАЯ МОДУЛЯЦИЯ

В случае амплитудной модуляции (AM) (t) в (2.56) является постоянной, a A(t) изменяется пропорционально модулирующему сигналу сообщения c(t):

, (2.57)

где k_АМ – коэффициент передачи модулятора.

Если c(t) – действительная функция, то (2.57) упрощается и принимает следующий вид:

, (2.58)

Процесс амплитудной модуляции иллюстрируется на рис. 2.4. Заметим, что здесь изменение полярности (знака) c(t) приводит к изменению фазы несущей модулированного сигнала на  радиан.

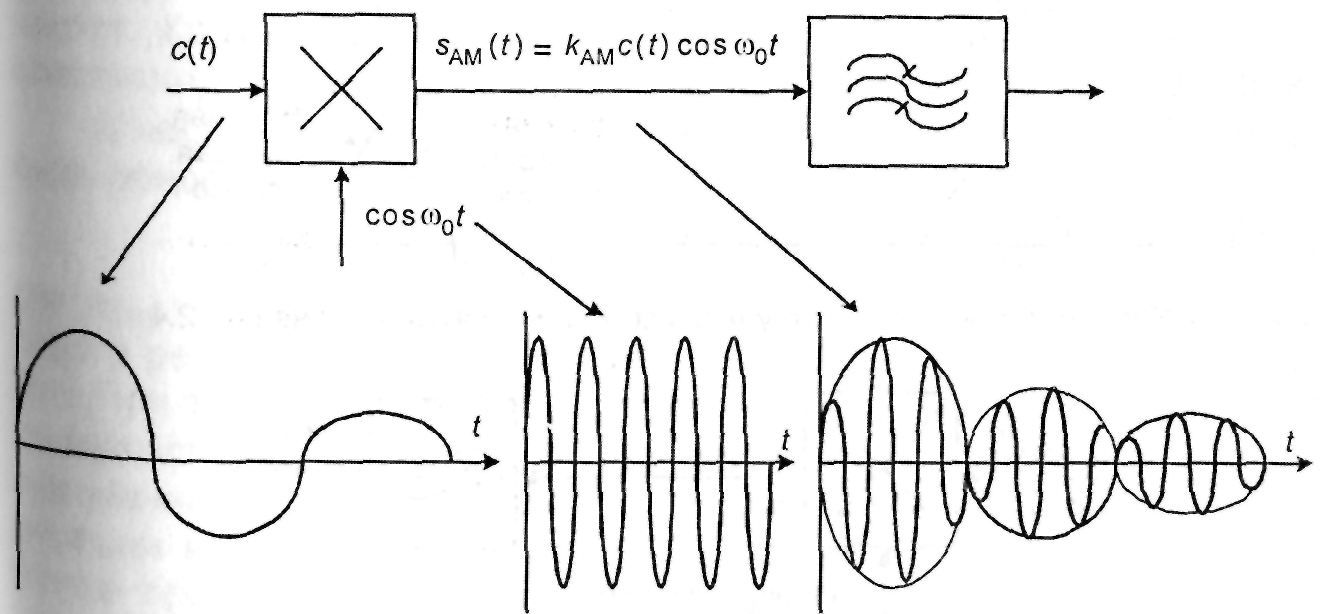
Рис. 2.4. Иллюстрация формирования сигналов с амплитудной модуляцией и подавленной несущей

Спектральная функция AM сигнала получается путем преобразования Фурье (2.58) и имеет следующий вид:

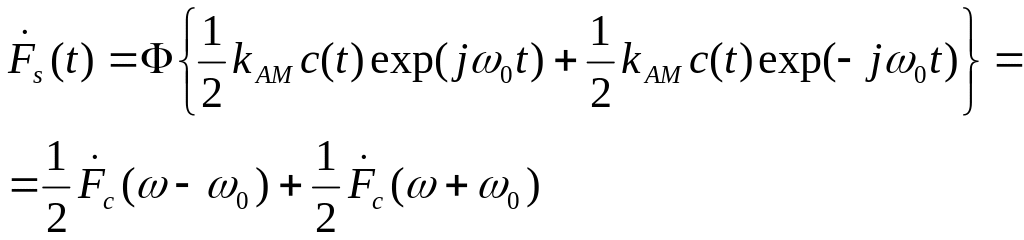, (2.59)

где – спектральная функция модулирующего сигнала, k_АМ = 1.

Заметим, что при таком выборе коэффициента k_АМ в процессе амплитудной модуляции происходит перенос спектра модулирующего сигнала на частоты ±₀ без его изменения. Эта разновидность амплитудной модуляции получила название амплитудной модуляции с двумя боковыми полосами и подавленной несущей (АМ-ДБП-ПН), поскольку спектр модулированного сигнала не содержит несущей, а боковые полосы сосредоточены вокруг частот ±₀ Если рассматривать только положительные частоты, имеющие физический смысл, то в результате амплитудной модуляции требуемая полоса частот увеличивается вдвое. Это показано на рис.2.5. Спектральные составляющие, расположенные выше частоты ₀, образуют так называемую верхнюю боковую полосу, а спектральные составляющие, расположенные ниже частоты ₀ – нижнюю боковую полосу.

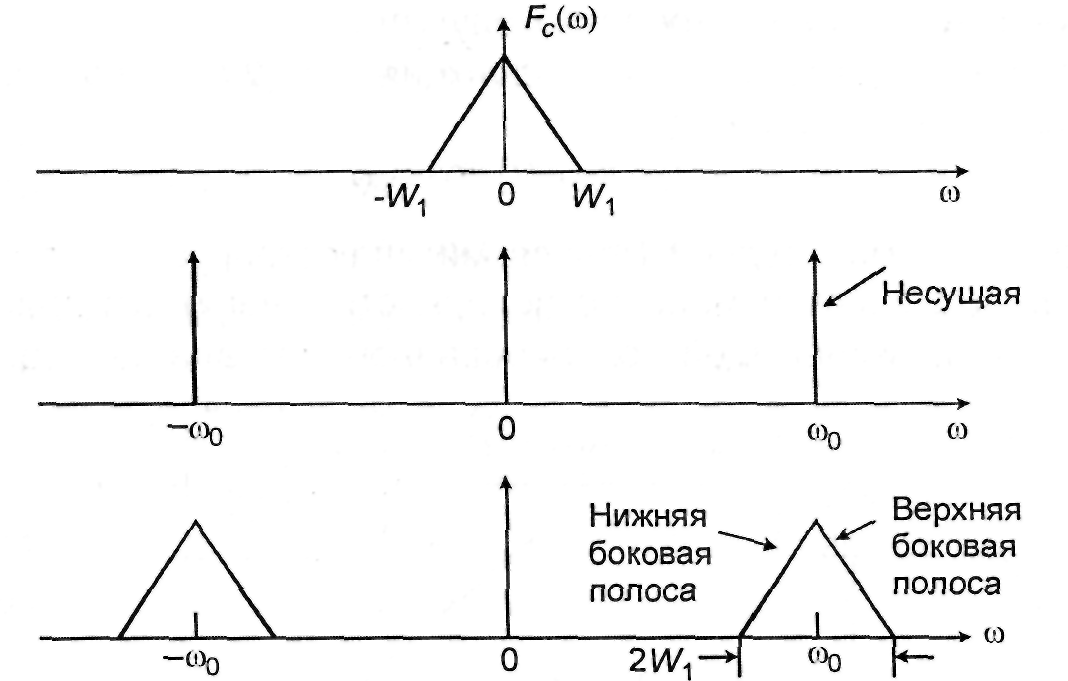
Рис.2.5. Спектральные функции сигналов, показанных на рис.2.4

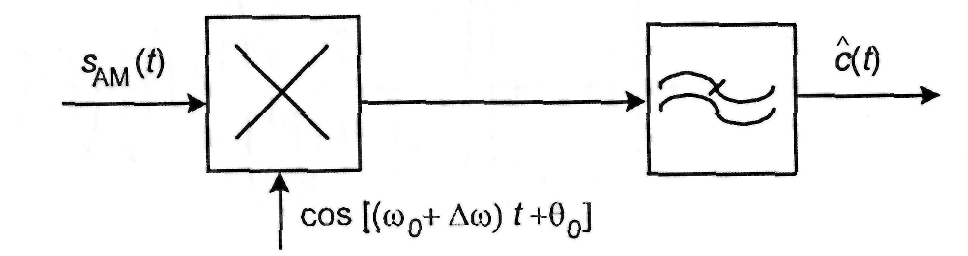
Рис. 2.6. Когерентный демодулятор (синхронный детектор) сигналов с амплитудной модуляцией и подавленной несущей

Демодуляция АМ-ДБП-ПН сигнала осуществляется путем его перемножения на опорный сигнал несущей и последующей низкочастотной фильтрации, как показано на рис. 2.6.

, (2.60)

Наличие фазовой ошибки ₀ в опорном сигнале несущей приводит только к уменьшению уровня демодулированного сигнала, частотная ошибка  приводит к недопустимым мультипликативным искажениям. Поэтому для демодуляции АМ-ДБП-ПН сигнала необходимо использовать синхронный демодулятор (синхронный детектор).

Использование АМ-ДБП-ПН требует наличия в демодуляторе опорного сигнала несущей, совпадающего с несущей демодулированного сигнала с точностью до начальной фазы. А поскольку сигнал несущей в АМ-ДБП-ПН отсутствует, то для восстановления необходимо дополнительные средства. Это несколько усложняет схему демодулятора. Чтобы избежать этого, можно к АМ-ДБП-ПН сигналу добавить сигнал немодулированной несущей с таким уровнем, чтобы в нем отсутствовали скачки фазы на , вызванные изменениями полярности модулирующего сигнала. В этом случае получим другую разновидность амплитудной модуляции, которая получила название амплитудной модуляции двумя боковыми полосами (АМ-ДБП), или просто AM. Математически АМ-ДБП сигнал может быть представлен в следующем виде:

, (2.61)

При соответствующем выборе значения А₀ амплитуда (огибающая) A(t) модулированного сигнала будет пропорциональна c(t). Процесс демодуляции в этом случае упрощается и сводится к выделению огибающей с помощью диодного детектора и фильтра нижних частот. Кроме того, здесь необходимо исключить постоянную составляющую, обусловленную наличием немодулированной несущей.

В частном случае, когда , выражение (2.61) может быть представлено в виде

, (2.62)

где – индекс амплитудной модуляции, с помощью которого регулируется соотношение уровней несущей и боковых полос. При значениях индекса модуляции, меньших 100 %, изменения полярности c(t) не вызывают скачков фазы несущей на , и модулированный сигнал отображает эти изменения. Поэтому для демодуляции вместо синхронного детектора может быть использован более простой детектор огибающей, правда, за счет ухудшения частотной характеристики в области низких частот и снижения энергетической эффективности.

Если не ограничиваться рассмотрением в качестве модулирующих сигналов действительных функций времени, то согласно (2.57) получим

, (2.63)

где i(t) и q(t) – соответственно действительная и мнимая части модулирующего сигнала c(t). Используя известное тождество для комплексных величин

,

выражение (2.63) можно представить в следующем виде:

, (2.64)

Сигнал (2.64) можно рассматривать как сумму двух АМ-ДБП-ПН сигналов находящихся в квадратуре (ортогональных сигналов). Поскольку i(t) и q(t) являются медленно изменяющимися функциями времени по сравнению с , то они могут быть разделены и демодулированы с помощью двух синхронных детекторов.

Разновидность амплитудной модуляции, описываемая (2.64), получила название квадратурной амплитудной модуляции (КАМ). Система связи с квадратурной амплитудной модуляцией в упрощенном виде показана на рис. 2.7.

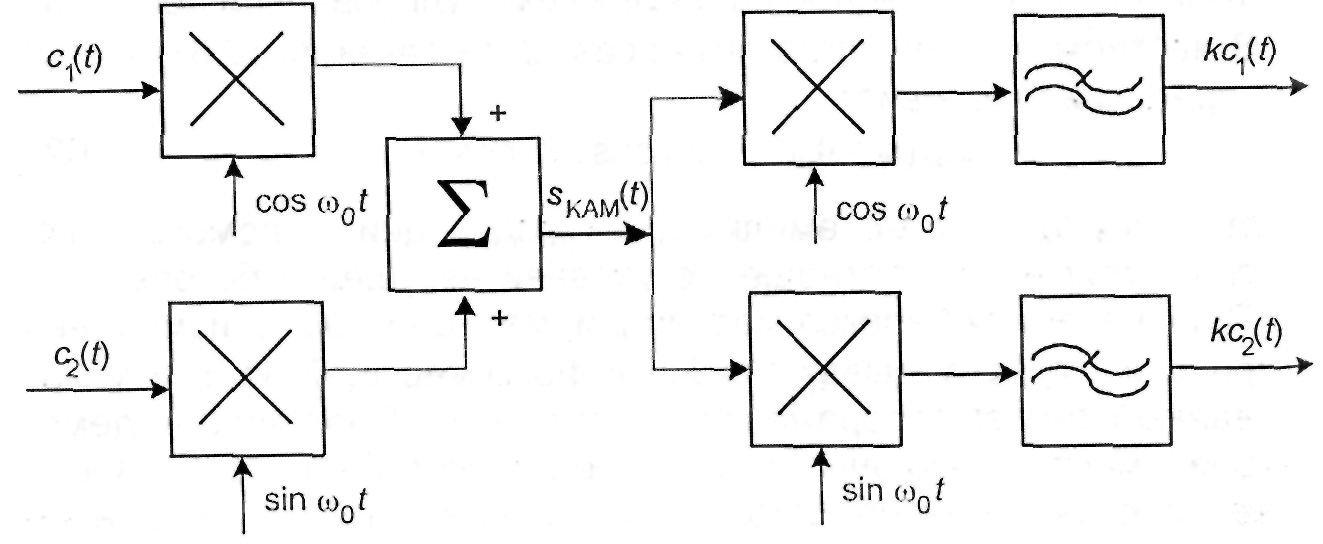
Рис. 2.7. Упрощенная схема системы связи с квадратурной амплитудной модуляцией

Рассмотренные разновидности амплитудной модуляции в лучшем случае требуют увеличения занимаемой полосы частот в два раза по сравнению с минимально необходимой для передачи сообщений с ограниченной полосой. Это их недостаток. Поэтому для экономии спектра желательно одну из боковых полос подавить. Принципиально подавление одной из боковых полос можно сделать с помощью фильтра одной боковой полосы (ОБП-фильтра). Однако требования, предъявляемые к подобному фильтру, оказываются достаточно жесткими. В идеальном случае он должен пропускать без искажений все спектральные составляющие одной боковой полосы и подавлять все спектральные составляющие другой. Амплитудно-частотная характеристика низкочастотного эквивалента такого идеального ОБП-фильтра должна иметь следующий вид:

, (2.65)

Ей соответствует комплексная частотная передаточная функция

, (2.66)

Для выполнения условия нечетности фазово-частотной характеристики ОБП-фильтра необходимо, чтобы

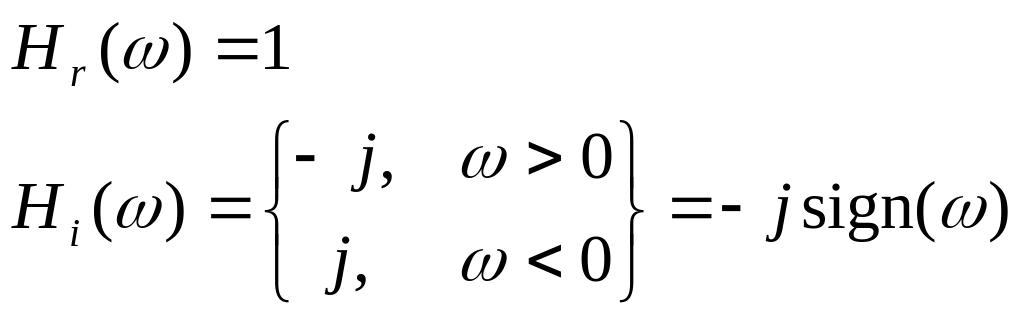, (2.67)

Здесь знаки неравенства определены для ОБП-фильтра выделяющего верхнюю боковую полосу. Если выделяется нижняя боковая полоса, то знаки неравенств необходимо поменять местами.

Импульсная характеристика ОБП-фильтра имеет вид

, (2.68)

Напомним, что . При воздействии на входе такого фильтра сигнала c(t) на его выходе будет формироваться отклик

, (2.69)

где – символ операции свертки двух функций.

Второе слагаемое в (2.69) представляет собой преобразование Гильберта функции c(t), которое обозначим . Согласно выражению (2.67) все спектральные составляющие приобретают дополнительный фазовый сдвиг на /2 по сравнению с аналогичными спектральными составляющими c(t), т.е. они находятся с ними в квадратуре.

Преобразование Гильберта не полностью определено при t = 0, поэтому в точках, где c(t) претерпевает разрывы первого рода, возникают бесконечные скачки амплитуды. Поэтому амплитудную модуляцию с одной боковой полосой (АМ-ОБП) целесообразно использовать, когда модулирующий сигнал представляет собой «гладкую» функцию времени. В этом случае огибающая не будет иметь значительных выбросов.

Комбинирование преобразования Гильберта и квадратурной амплитудной модуляции позволяет реализовать фазовый метод формирования АМ-ОБП сигнала, который представлен на рис. 2.8.

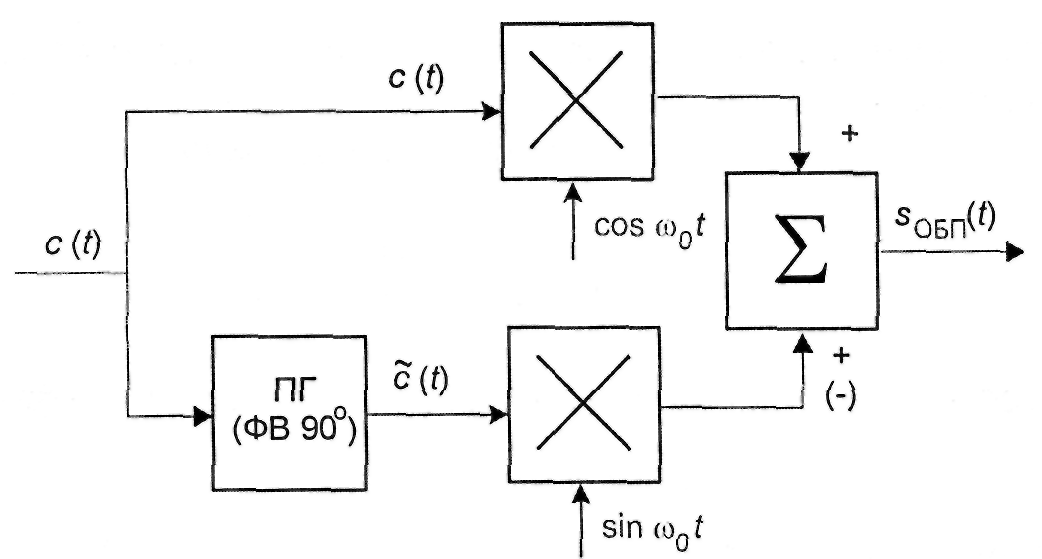
Рис. 2.8. Представление фазового метода формирования АМ-ОБП сигналов

Основной проблемой, которую необходимо решить при использовании фазового метода формирования АМ-ОБП сигнала, является построение фазовращателя, обеспечивающего фазовый сдвиг всех составляющих сигнала c(t) на /2. С математической точки зрения фильтровой и фазовый методы формирования АМ-ОБП эквивалентны, поэтому в любом случае АМ-ОБП сигнал может быть записан следующим образом:

, (2.70)

где знаки ( ) соответствуют нижней и верхней выделяемым боковым полосам.

Если АМ-ОБП сигнал (2.70) подать на вход синхронного детектора, то на его выходе будет формироваться сигнал, который может быть представлен в виде

, (2.71)

где  и – частотная и фазовая ошибки синхронизации.

Фазовые искажения, т.е. наложение c(t) на возникают, если . Кроме того, при имеет место частотный сдвиг всех составляющих.

При использовании синхронного детектора для демодуляции АМ-ОБП сигналов при наличии ошибок синхронизации происходит ухудшение качества демодуляции, но оно существенно меньше по сравнению с тем, которое обусловлено мультипликативными искажениями при демодуляции АМ-ДБП-ПН сигналов.

Таким образом, АМ-ОБП позволяет за счет некоторого снижения качества передачи в два раза сократить требуемую полосу частот при передаче.

Существует еще одна разновидность амплитудной модуляции, получившая название амплитудной модуляции с частично-подавленной боковой полосой (АМ-ЧПБП). В этом случае обеспечивается компромисс между требуемой полосой передачи в случае АМ-ОБП и АМ-ДБП-ПН.

Модулятор сигналов АМ-ЧПБП содержит обычный АМ-ДБП-ПН модулятор и фильтр частично-подавленной боковой полосы (ЧПБП-фильтр) с амплитудно-частотной характеристикой . Сигнал АМ-ЧПБП имеет спектральную плотность

. (2.72)

При воздействии АМ-ЧПБП сигнала на вход синхронного детектора на его выходе формируется сигнал сообщения

. (2.73)

Таким образом, для неискаженного воспроизведения сигнала сообщения c(t) необходимо, чтобы выполнялось условие

. (2.74)

где – верхняя частота спектра модулирующего сигнала.

Если постоянную в (2.74) положить равной то можно убедиться, что амплитудно-частотная характеристика ЧПБП фильтра должна быть асимметричной относительно частоты несущей . Хотя при получении этого результата предполагалось использование синхронного детектора, он остается справедливым и в случае использования детектора огибающей, если «остаток» несущей имеет достаточный уровень.

Амплитудная модуляция с частично-подавленной боковой находит широкое применение в телевизионных системах для передачи сигналов изображения.

УГЛОВАЯ МОДУЛЯЦИЯ

В общем случае между фазой и мгновенной частотой квазигармонического колебания имеют место следующие соотношения:

, (2.75)

. (2.76)

Это определение частоты, вообще говоря, отличается от того, которое принято в спектральном анализе, где частоты не могут изменяться во времени.

При угловой модуляции в (2.56) мы полагаем постоянной амплитуду, и в соответствии с модулирующим сигналом c(t) изменяется фазовый угол. В случае прямой пропорциональности

, (2.77)

и этот вид угловой модуляции носит название фазовой (ФМ).

Если прямо пропорционально модулирующему сигналу изменяется мгновенная частота:

, (2.78)

то такой вид угловой модуляции носит название частотной (ЧМ). Если модуляция осуществляется гармоническим сигналом

, (2.79)

то мгновенная частота изменяется по закону

, (2.80)

где k_ЧМ – коэффициент передачи частотного модулятора, имеющий размерность радиан на секунду-вольт [рад/(сВ)].

Вводя новый параметр , так называемую пиковую частотную девиацию (частотное отклонение несущей), (2.80) можно представить в следующем виде:

, (2.81)

Изменения фазы ЧМ сигнала при гармоническом модулирующем сигнале определяются выражением, которое следует из (2.75) и (2.81):

, (2.82)

где – индекс частотной модуляции.

Согласно (2.56) ЧМ сигнал аналитически может быть представлен как

, (2.83)

В (2.83) второй экспоненциальный сомножитель являет периодическую функцию (с основной частотой ), поэтому он может быть представлен в виде ряда Фурье. В этом случае

, (2.84)

где – функция Бесселя первого рода, n-гo порядка.

Используя свойства указанных функций Бесселя, можно получить следующее приближенное соотношение, определяющее ширину спектра или требуемую полосу частот ЧМ сигнала:

, (2.85)

Согласно (2.85) ширина спектра ЧМ сигнала зависит от индекса частотной модуляции и при больших значениях существенно превышает ширину спектра AM сигнала. Поэтому частотную модуляцию относят к видам модуляции с расширением спектра сигнала.

Демодуляцию ЧМ сигналов можно осуществить при помощи либо схем, обеспечивающих преобразование отклонений частоты от частоты несущей в изменения уровня, либо схем с обратной связью, примером которой может служить схема фазовой синхронизации. При использовании схем фазовой синхронизации качество демодуляции получается наиболее высоким, и при этом не требуется наличия резонансных элементов.

При фазовой модуляции гармоническим сигналом выражение (2.77) принимает вид

, (2.86)

где – пиковая фазовая девиация, – коэффициент передачи фазового модулятора, имеющий размерность радиан на вольт (рад/В).

Вычислив производную от (2.86) и сравнив полученный результат с (2.81), заметим, что в случае фазовой модуляции пиковая девиация частоты пропорциональна не только амплитуде модулирующего сигнала, но и его частоте, т.е.

(2.87)

При представлении ФМ сигнала в виде ряда Фурье (2.84) численное значение индекса модуляции  равно пиковому значению фазовой девиации , поэтому ширина спектра ФМ сигнала определяется выражением (2.85), в котором вместо величины  следует подставить величину .