3.2. Блоковые коды

Если обозначить вероятность ошибки при приеме символов в системах без кодирования и с блоковым кодированием соответственно р₀ и p₁ то вероятности ошибочного приема в системе без кодирования и с кодированием будут определяться соответственно выражениями:

, (3.1)

, (3.2)

Здесь предполагается, что код имеет минимальное Хэммингово расстояние d_min и исправляет все ошибки кратности

,

– количество возможных конфигураций из n символов, содержащих i ошибок.

Между параметрами n, k и t блокового кода существует определенное соотношение, устанавливаемое так называемой границей Хэмминга

, (3.3)

Коды, для которых соотношение (3.3) выполняется строго, называются совершенными. Примером совершенных кодов служит код Хэмминга, исправляющий одиночные ошибки, и код Голея. Другие коды могут исправлять некоторые конфигурации ошибок, кратность которых превышает t. Для этих кодов (3.3) следует трактовать как полезную верхнюю границу.

В табл.3.1 приведены примеры блоковых кодов, исправляющих ошибки кратности t, и их параметры.

Таблица 3.1

Кратность исправляемых ошибок и минимальное расстояние	n	k	Код	Кодовая скорость (Rk=k/n)
t = 1, dmin = 3	3	1	(3,1)	0,33
	4	1	(4,1)	0,25
	5	2	(5,2)	0,4
	6	3	(6,3)	0,5
	7	4	(7,4)	0,57
	15	11	(15,11)	0,73
	31	26	(31,26)	0,838
t = 2, dmin = 5	10	4	(10,4)	0,4
	15	8	(15,8)	0,533
t = 3, dmin =7	10	2	(10,2)	0,2
	15	5	(15,5)	0,33
	23	12	(23,12)	0,52

Блоковые коды можно использовать и для обнаружения ошибок кратности и. В этом случае минимальное Хэммингово расстояние между словами кода должно быть

d_min = u + 1.

Если блоковый код предназначен для исправления и обнаружения ошибок кратности t и и соответственно, то минимальное кодовое расстояние должно удовлетворять условию

d_min  t + u + 1.

3.3. Основные классы блоковых кодов

КОД ПОВТОРЕНИЙ

Блоковый код вида (n,1) известен как код повторений. В нем значение информационного символа повторяется (n–1) раз, т.е. (n–1) проверочных символов являются повторением информационного. Кодовая скорость равна 1/n и при достаточно больших n оказывается крайне низкой. Минимальное расстояние кода равно n и при достаточно больших n коды повторений обладают высокой исправляющей способностью. Поскольку минимальное расстояние равно n, то кратность исправляемых ошибок в кодовом слове будет составлять t = (n – 1)/2. Вероятность ошибочного декодирования

, (3.4)

При n = 5

, (3.5)

Для достаточно малых значений р₁

, (3.6)

линейные блоковые коды

В линейном блоковом коде l-й символ кодового слова

представляет собой линейную комбинацию k информационных символов. В матричной форме записи

, (3.7)

где G – порождающая матрица кода, содержащая k строк и n столбцов

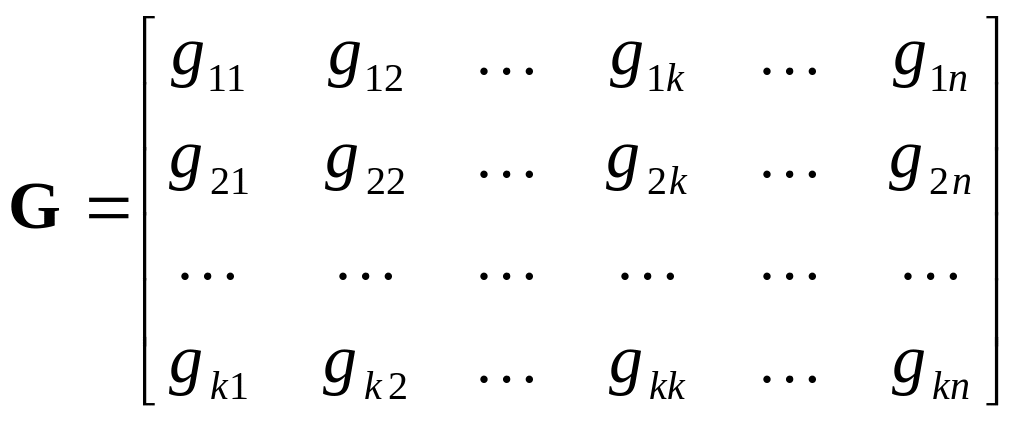, (3.8)

Таким образом, процедура конструирования кода сводится к определению элементов g_ii порождающей матрицы.

Поскольку для систематического кода первые k символов кодового слова В являются информационными символами слова А, т.е. b=а, g_il =1, i = l, то порождающая матрица кода имеет вид

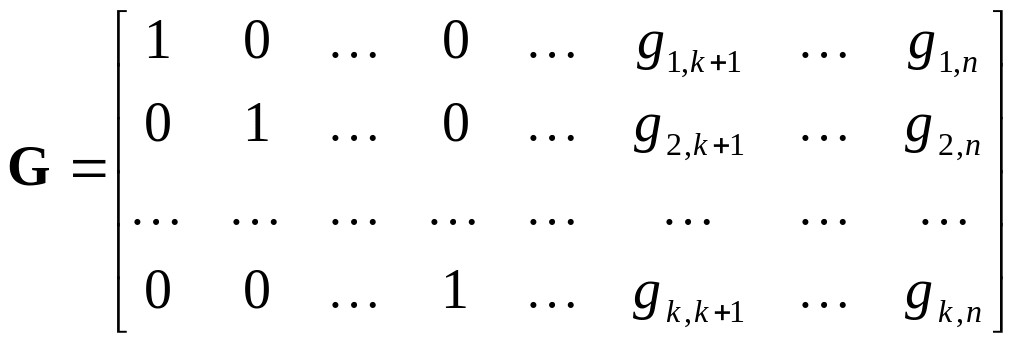, (3.9)

или

, (3.10)

где I – единичная матрица kk; Р представляет последние (n–k) столбцов порождающей матрицы.

С порождающей матрицей линейного кода связана так называемая проверочная матрица H:

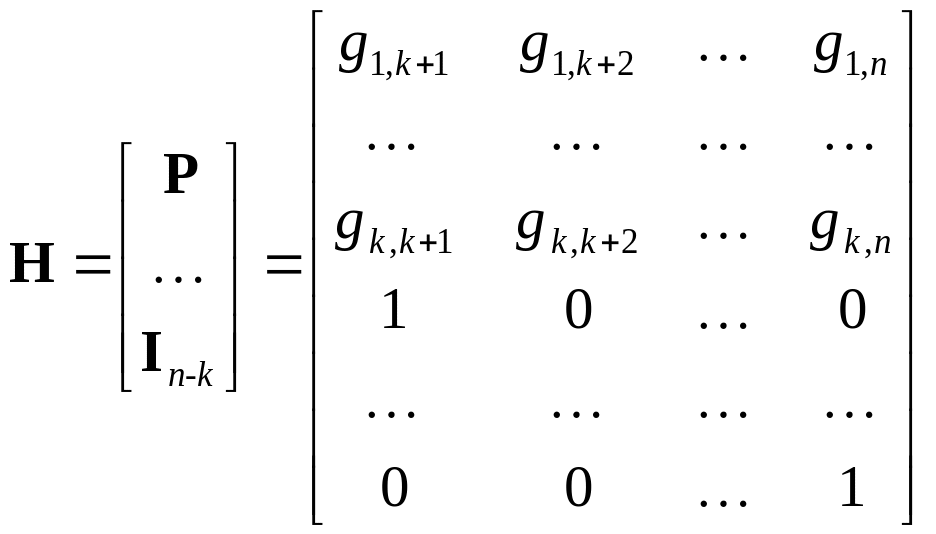, (3.11)

Декодирование линейного кода осуществляется умножением выходной последовательности Z демодулятора на проверочную матрицу Н, в результате которого формируется слово, так называемый синдром S:

,

Для двоичных кодов выходная последовательность Z может быть представлена в виде суммы по модулю 2 переданного кодового слова В и вектора ошибок Е. Поэтому синдром может быть представлен как

, (3.12)

Согласно (3.10) j-й элемент S¹ может быть записан как

. (3.13)

Для систематических кодов b_i = a_i, i ≤ k, поэтому

. (3.14)

Из уравнения (3.10) следует, что

. (3.15)

Следовательно,

. (3.16)

Поскольку все (n-k) элементов S⁽¹⁾ равны нулю, то

, (3.17)

и синдром определяется соотношением

, (3.18)

Таким образом, синдром, состоящий из всех нулей, означает, что принятая последовательность принадлежит множеству кодовых слов линейного кода. Это означает, что при приеме либо не произошло ни одной ошибки, либо конфигурация ошибок оказалась такой, что трансформировала переданное кодовое слово в другое кодовое слово. Если минимальное кодовое расстояние кода равно d_min, то должно произойти по крайней мере d_min ошибок при трансформации одного кодового слова в другое.

Процесс декодирования заключается в определении для каждого синдрома вектора ошибок минимального веса, удовлетворяющего уравнению . Этот вектор ошибок суммируется по модулю 2 с принятой последовательностью Z.

В результате формируется наиболее вероятное слово. Рассмотренный метод декодирования получил название синдромного и может быть реализован с помощью ПЗУ.

КОДЫ ХЭММИНГА

Эти коды являются примером линейных кодов, исправляющих одну единственную ошибку. Длина блока кодов удовлетворяет соотношению n = 2^(n-k)–1, где n – k количество проверочных символов. Например, при n – k =3 получаем код (7, 4).

ЦИКЛИЧЕСКИЕ КОДЫ

Эти коды также относятся к классу линейных блоковых кодов и являются наиболее распространенными. Особенность этих кодов состоит в том, что если некоторое кодовое слово принадлежит коду, то и его циклические перестановки также принадлежат коду.

Иными словами (n – 1) кодовых слов могут быть сформированы путем циклического сдвига одного кодового слова. Все множество кодовых слов может быть получено в результате циклических сдвигов различных кодовых слов. Достоинство этого класса кодов заключается в относительно простой аппаратурной реализации кодеков, основными элементами которой являются регистры сдвига и сумматоры по модулю 2.

Кодирование и вычисление синдрома при декодировании могут быть осуществлены с помощью либо k-разрядного, либо (n – k) – разрядного сдвига.

В классе циклических кодов наиболее важен подкласс так называемых кодов БЧХ. Эти коды могут быть построены для широких диапазонов длины блока, кодовой скорости и исправляющей способности. В частности, если t – кратность исправляемых ошибок в пределах блока, т – произвольное целое число, то длина кодового слова, количество проверочных символов и кодовое расстояние удовлетворяют соотношениям:

n = 2^m–1; n – k ≤ mt; d > 2t – 1.

В табл. 3.2 в качестве примера приведены соотношения между параметрами некоторых кодов БЧХ. Отметим, что при t = 1 параметры n и k соответствуют параметрам кода Хэмминга. Иначе говоря, код Хэмминга также является кодом БЧХ, исправляющим одиночные ошибки.

Таблица 3.2

n	k	t	n	k	t	n	k	t	n	k	t
7	4	1	127	120	1	255	247	1	255	99	23
15	11	1	127	113	2	255	239	2	255	91	25
15	7	2	127	106	3	255	231	3	255	87	26
31	26	1	127	99	4	255	223	4	255	79	27
31	21	2	127	92	5	255	215	5	255	71	29
31	16	3	127	85	6	255	207	6	255	63	30
31	11	5	127	78	8	255	199	7	255	55	31
63	57	1	127	71	9	255	191	8	255	47	42
63	51	2	127	64	10	255	187	9	255	45	43
63	45	3	127	57	11	255	179	10	255	37	45
63	39	4	127	50	13	255	171	11	255	29	47
63	36	5	127	8	31	255	163	12
63	10	13				255	115	21
63	7	15				255	107	22

КОДЫ РИДА-СОЛОМОНА

Коды Рида-Соломона (коды PC) относятся к классу недвоичных кодов БЧХ. В кодере сообщение, состоящее из k q-ичных символов, выбираемых из алфавита, содержащего q = 2^m символов, преобразуется в кодовое слово PC-кода, содержащее n двоичных символов. Поскольку обычны входного и выходного алфавитов равны степени 2, то входные и выходные символы могут быть представлены m-разрядными двоичными словами. Таким образом, входное сообщение можно рассматривать как km-разрядное слово, а выходное кодовое слово – как nm-разрядное двоичное слово. Длина кода PC равна n = q – 1. Если исправляющая способность кода равна t ошибочным символам, то имеет место соотношение n – k = 2t. Коды PC существуют при 1 ≤ k ≤ n – 2, а их расширение имеет длины блока: n = q и n = q + 1.

КОД ГОЛЕЯ

Этот код относится к числу наиболее интересных. Он позволяет исправить ошибки высокой кратности (t > 1) и является также совершенным кодом. Код Голея (23, 12) является циклическим и исправляет все конфигурации ошибок, кратность которых не превышает трех. С кодом Голея (23, 12) связан код (24, 12), который образуется добавлением к кодовым словам кода (23, 12) дополнительного проверочного символа. Коды (23, 12) и (24, 12) имеют минимальное кодовое расстояние, равное соответственно 7 и 8. Поэтому код (24, 12), кроме исправления ошибок кратности 3, обеспечивает обнаружение ошибок кратности 4 при незначительном изменении кодовой скорости. Код (24, 12) относится в числу наиболее распространенных.