2.1. Представление сигналов и помех

ОСНОВНЫЕ СООТНОШЕНИЯ

Приведем основные аналитические соотношения, которые будем использовать в дальнейшем. При рассмотрении этих соотношений будем осуществлять временное и частотное представление функций времени (сигналов).

Для прямого преобразования Фурье (спектральной функции) сигнала s(t)

(2.1)

Для обратного преобразования Фурье –

. (2.2)

В ряде случаев для сокращения выкладок используется комплексное представление действительного сигнала s(t)

, (2.3)

где – сопряженный с s(t) сигнал, определяемый на основе преобразования Гильберта,

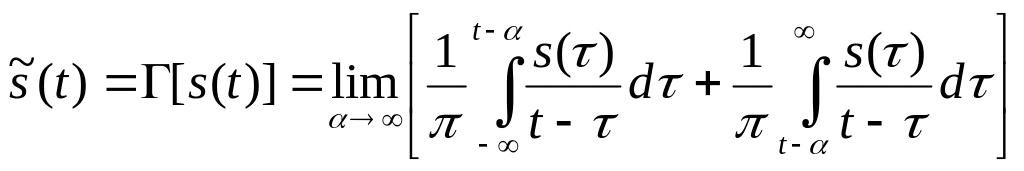. (2.4)

Представление s(t) в комплексной форме (2.3) называют представлением в аналитической форме или аналитическим сигналом.

Легко проверить, что , . Следовательно, если имеется сигнал сложной формы

(2.5)

то сопряженный ему сигнал

.

Таким образом, каждая гармоническая составляющая сопряженного сигнала повернута на угол /2 относительно соответствующей составляющей исходного сигнала s(t).

Применив (2.2) к , получим преобразование Фурье сопряженного сигнала

(2.6)

Спектральная функция комплексного сигнала

(2.7)

Следовательно, для получения спектральной функции комплексного сигнала необходимо удвоить спектральную функцию исходного сигнала s(t) при  > 0 и приравнять ее нулю при  < 0. Сигнал s(t), спектральная функция которого равна нулю за пределами некоторой полосы частот, так что

(2.8)

называется полосовым.

Для полосовых сигналов используется представление

(2.9)

где – огибающая полосового сигнала s(t);

– полная фаза. (2.10)

Если , то сигнал (2.10) называют узкополосным в спектральном смысле. Его можно представить в комплексной форме (2.3) как

, (2.11)

где

(2.12)

– комплексная огибающая (комплексная амплитуда) сигнала.

Узкополосный сигнал можно рассматривать в виде суммы двух квадратурных составляющих:

(2.13)

где

, , (2.14)

с помощью которых определяется мгновенная частота

. (2.15)

Между преобразованиями сигналов и имеет место соотношение

(2.16)

Представление узкополосных сигналов через комплексную огибающую можно распространить и на так называемые узкополосные системы. Узкополосными системами называются такие системы, отклик которых на произвольный входной сигнал s(t) является узкополосным сигналом.

Пусть линейная узкополосная система с постоянными параметрами имеет импульсную характеристику h(t) и частотную передаточную функцию . Импульсную характеристику h(t) можно также представить в комплексной форме: . Ей соответствует частотная передаточная функция , где согласно (2.7) есть частотная передаточная функция идеального фильтра верхних частот, пропускающего все «положительные» частоты.

Таким образом, отклик узкополосной системы в комплексной форме на входной сигнал s(t) может быть получен как выходной сигнал последовательно включенных рассматриваемой узкополосной системы и фильтра верхних частот с частотной передаточной функцией . Поскольку все операции являются линейными, то порядок их выполнения может быть произвольным, как показано на рис.2.1.

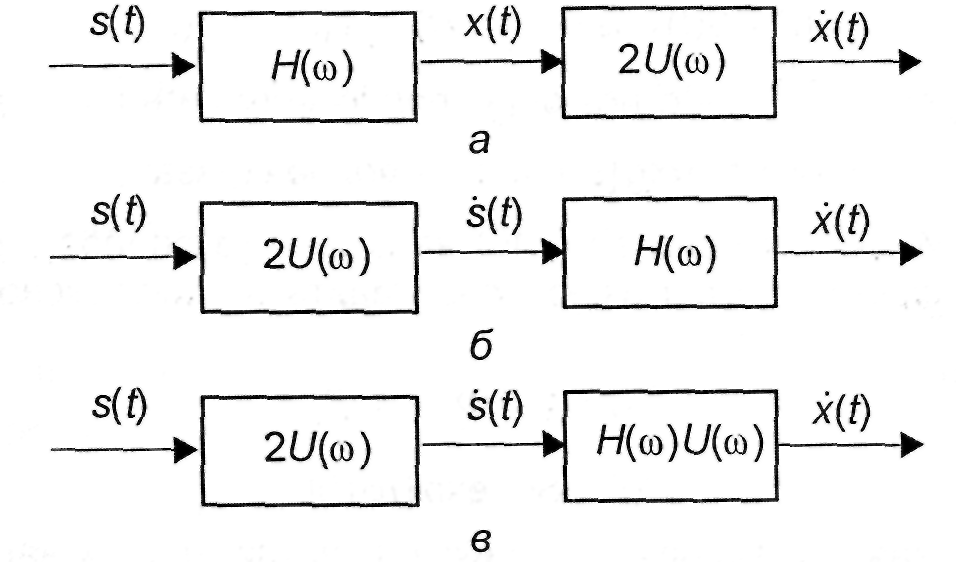
Рис. 2.1. Три эквивалентные схемы представления аналитического сигнала, соответствующего отклику линейной системы с постоянными параметрами

В варианте (рис.2.1, в) линейная система имеет комплексную импульсную характеристику , поэтому ее отклик на комплексный сигнал определяется выражением

. (2.17)

Если и выразить через комплексные огибающие (2.12), то

, (2.18)

– комплексная огибающая импульсной характеристики.

Из (2.18) следует, что отклик узкополосной линейной системы с постоянными параметрами представляет собой узкополосный сигнал с комплексной огибающей

. (2.19)

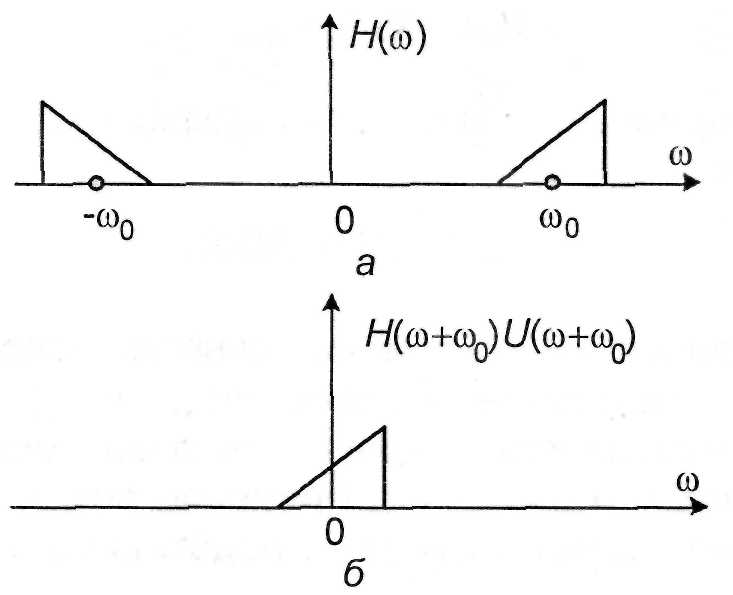
Рис. 2.2. Частотная передаточная функция узкополосной линейной системы (а) и ее низкочастотного эквивалента (б)

Таким образом, комплексная огибающая отклика узкополосной системы может быть найдена как результат обработки комплексной огибающей входного сигнала эквивалентной низкочастотной линейной системой с комплексной импульсной характеристикой и частотной передаточной функцией , как показано на рис.2.2.

Заметим, что если симметрична относительно частоты , то низкочастотный эквивалент узкополосной линейной системы имеет действительную импульсную характеристику.

ДИСКРЕТНОЕ ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ

Реальные сигналы, присутствующие в устройствах и системах связи, являются на определенных интервалах непрерывными функциями времени. Однако при анализе часто удобно использовать их представление в виде выборочных мгновенных значений, т.е. в виде рядов по системам ортонормальных функций, коэффициентами при которых являются выборочные значения.

Пусть имеется n независимых сигналов . Независимость сигналов означает, что ни один из этих сигналов не может быть представлен в виде линейной комбинации остальных (n – 1) сигналов, т.е. не существует постоянных a₁, a₂, …, a_n (не равных нулю), таких, что

. (2.20)

Эти сигналы образуют базис.

Предположим, что сигнал s(t) может быть представлен в виде линейной комбинации n независимых сигналов :

. (2.21)

Если каждый сигнал может быть представлен в виде (2.21), то мы имеем n-мерное пространство сигналов. Множество сигналов называется ортонормальным, если выполняется условие

(2.22)

Для ортонормального множества коэффициенты s_k в (2.21) определяются как

. (2.23)

При выбранном множестве базисных сигналов сигнал s(t) может быть представлен набором чисел (s₁, s₂, …, s_n) или точкой в n-мерном пространстве. Теперь сигнал s(t) может рассматриваться как вектор s = (s₁, s₂, …, s_n). Примером дискретного представления сигналов может служить представление в виде ряда В.А. Котельникова

(2.24)

где sinc(x) = sin(x)/x, В – верхняя частота спектра сигнала s(t).

Здесь в качестве ортонормальных функций выбраны функции

.

Легко проверить, что

(2.25)

При этом

(2.26)

(2.27)

Таким образом, любой сигнал s(t) с ограниченным спектром может быть представлен точкой в пространстве сигналов с координатами (…, s_k‑1, …, s_‑2, s_‑1, s₀, s₁, s₂, …, s_k, …), s_k – значение k-го отсчета, деленное на .

Рассмотрим теперь четыре сигнала:

.

Если в качестве ортонормальных функций выбрать функции , , то эти сигналы могут быть представлены в виде векторов , , , и размерность пространства сигналов равна двум.

Если в пространстве сигналов сигналы s₁(t) и s₂(t) представлены векторами s₁ = (s₁₁, s₁₂, …, s_1n) и s₁ = (s₂₁, s₂₂, …, s_2n), причем , , то

. (2.28)

Таким образом, интеграл от произведения двух сигналов есть скалярное произведение векторов в пространстве сигналов, и взаимной ортогональности двух функций времени соответствует ортогональность векторов при их дискретном представлении.

Для сигнала s(t) энергия E_s определяется выражением

. (2.29)

Из соотношения (2.28) следует, что

. (2.30)

где |s|² – квадрат длины вектора s.

Следовательно, энергия сигнала равна квадрату длины соответствующего вектора в пространстве сигналов.

Итак, размерность пространства сигналов равна максимальному количеству независимых векторов в этом пространстве. В n-мерном пространстве может быть не более, чем n независимых векторов. Если найдено множество из n независимых ректоров, то можно с помощью процедуры Грама-Шмидта построить другое множество из n независимых векторов, которые являются взаимно ортогональными и образуют координатную систему.

ГАУССОВСКИИ СЛУЧАЙНЫЙ ПРОЦЕСС

Случайный процесс (t) называется гауссовским, если совокупность случайных величин (t₁), (t₂), … (t_n), определенных для моментов времени t₁, t₂, … t_n, является совместно гауссовской, т.е. имеем совместную функцию плотности распределения вероятности (ФПРВ), определяемую выражением

, (2.31)

где K – ковариационная матрица,

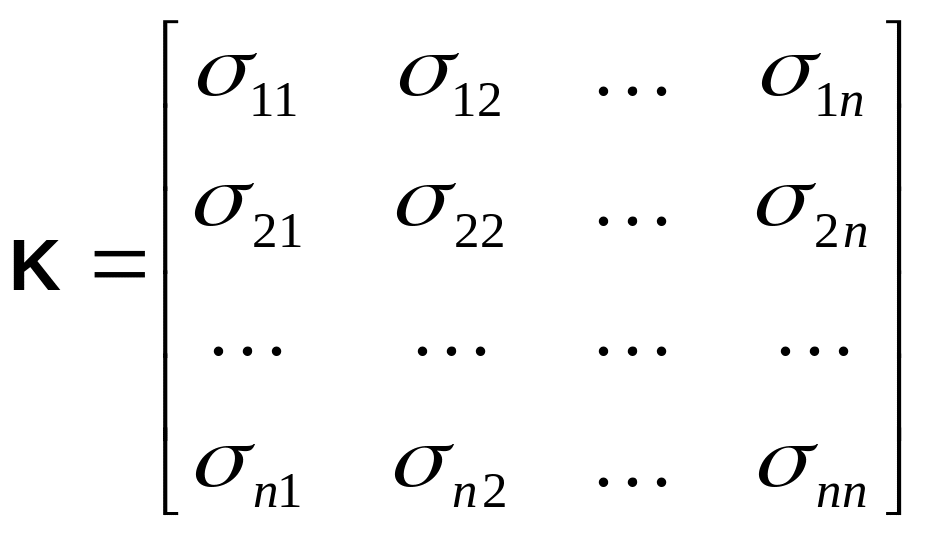, (2.32)

– ковариация случайных величин _i и _j, – математическое ожидание случайной величины _i |K| – определитель матрицы K, K_ij алгебраическое дополнение элемента в матрице K. Заметим, что – дисперсия случайной величины _i .

Гауссовский случайный процесс не только представляет весьма удобную модель случайных процессов, которые встречаются в реальных ситуациях, но и обладает рядом свойств, позволяющих упростить получение некоторых математических, важных с практической точки зрения, результатов.

Из (2.31) следует, что гауссовский случайный процесс полностью определяется корреляционной функцией

, (2.33)

и математическим ожиданием , так как .

Гауссовский случайный процесс называется стационарным, если выполняются условия

для всех t. (2.34)

Условия (2.34) являются условиями стационарности в широком смысле, поэтому для гауссовского случайного процесса они являются условиями строгой стационарности.

Для стационарного гауссовского случайного процесса ковариация определяется следующим выражением:

. (2.35)

Другим важным свойством гауссовского случайного процесса является то, что отклик линейной системы на воздействие в виде гауссовского случайного процесса также гауссовский случайный процесс.

Пусть на входе линейной системы с импульсной характеристикой h(t) имеется гауссовский случайный процесс (t). Тогда случайный процесс на выходе системы

. (2.36)

Поскольку (t) – гауссовский процесс, то все случайные величины (t-_k) являются совместно гауссовскими (по определению). Следовательно, случайные величины (t₁), (t₂), … (t_n), определенные для моментов времени t₁, t₂, … t_n, есть линейные комбинации совместно гауссовских случайных величин и также являются совместно гауссовскими. Таким образом, случайный процесс (t) является гауссовским.

Если имеется полное множество ортонормальных базисных функций {_k(t)}, то в пространстве сигналов реализация х(t) гауссовского случайного процесса может быть представлен в виде ряда

, (2.37)

где

.

Заметим, что случайный процесс (t) состоит из множества реализаций x(t). Поэтому для каждой реализации имеется собственный коэффициент. Отсюда следует, что значения коэффициентов (x₁, x₂, … x_n) – это значения случайных величин (₁, ₂, … _n), полученные для определенной реализации с функцией плотности распределения вероятности .

Рассмотрим в качестве примера гауссовский случайный процесс h(t) в виде белого шума со спектральной плотностью N₀/2 и корреляционной функцией , – дельта-функция. Представим n(t) в виде ряда

Так как белый шум имеет неограниченную полосу, то размерность пространства сигналов также неограниченна.

Покажем, что n₁, n₂, … – независимые случайные величины с дисперсией N₀/2. Действительно,

,

Так как

,

то, используя правило интегрирования с -функцией, получаем

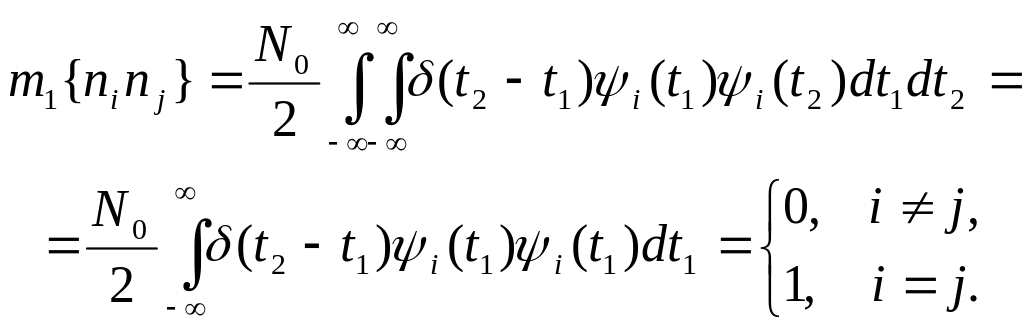(2.38)

Следовательно случайные величины n_i и n_j некоррелированны, а поскольку они являются гауссовскими, то и независимы.

Если ограничиться представлением белого шума в виде конечного ряда, т.е. ограничить размерность пространства сигналов, то функция плотности распределения вероятности совокупности случайных величин n₁, n₂, … n_N будет определяться следующим выражением:

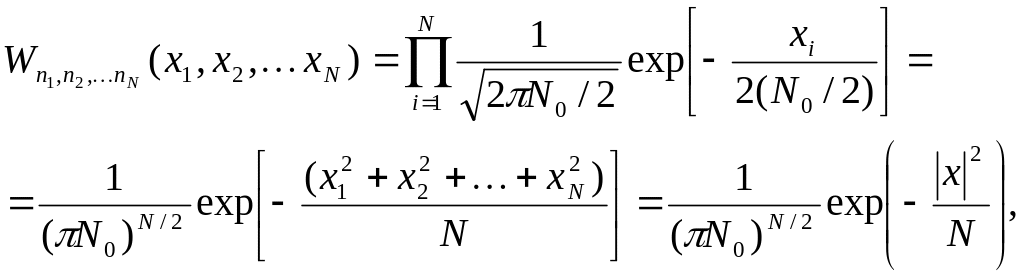(2.39)

Из (2.39) следует, что ФПРВ белого гауссовского шума зависит только от длины шумового вектора х в пространстве сигналов и поэтому обладает свойством сферической симметрии.

УЗКОПОЛОСНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС

Рассмотрим теперь действительный, стационарный в широком смысле случайный процесс n(t) и комплексный процесс . Существуют следующие формы представления этих процессов:

, (2.40)

, (2.41)

, (2.42)

, (2.43)

где – комплексная огибающая случайного процесса n(t).

Спектральная плотность процесса может быть легко определена, если учесть, что он формируется на выходе линейной системы с постоянными параметрами и частотной передаточной функцией 2U(f). Поэтому получаем

, (2.44)

Из выражения (2.44) следует, что спектральная плотность комплексного процесса равна учетверенной односторонней спектральной плотности действительного процесса n(t).

Корреляционная функция комплексной огибающей равна

, (2.45)

где (..) – символ комплексного сопряжения. Следовательно, спектральная плотность

, (2.46)

и совпадает со спектральной плотностью комплексного процесса, перенесенной в начало координат. Это отражено на рис.2.3.

Можно показать, что авто- и взаимно-корреляционные функции квадратурных составляющих n_I(t) и n_Q(t) удовлетворяют следующим соотношениям:

, (2.47)

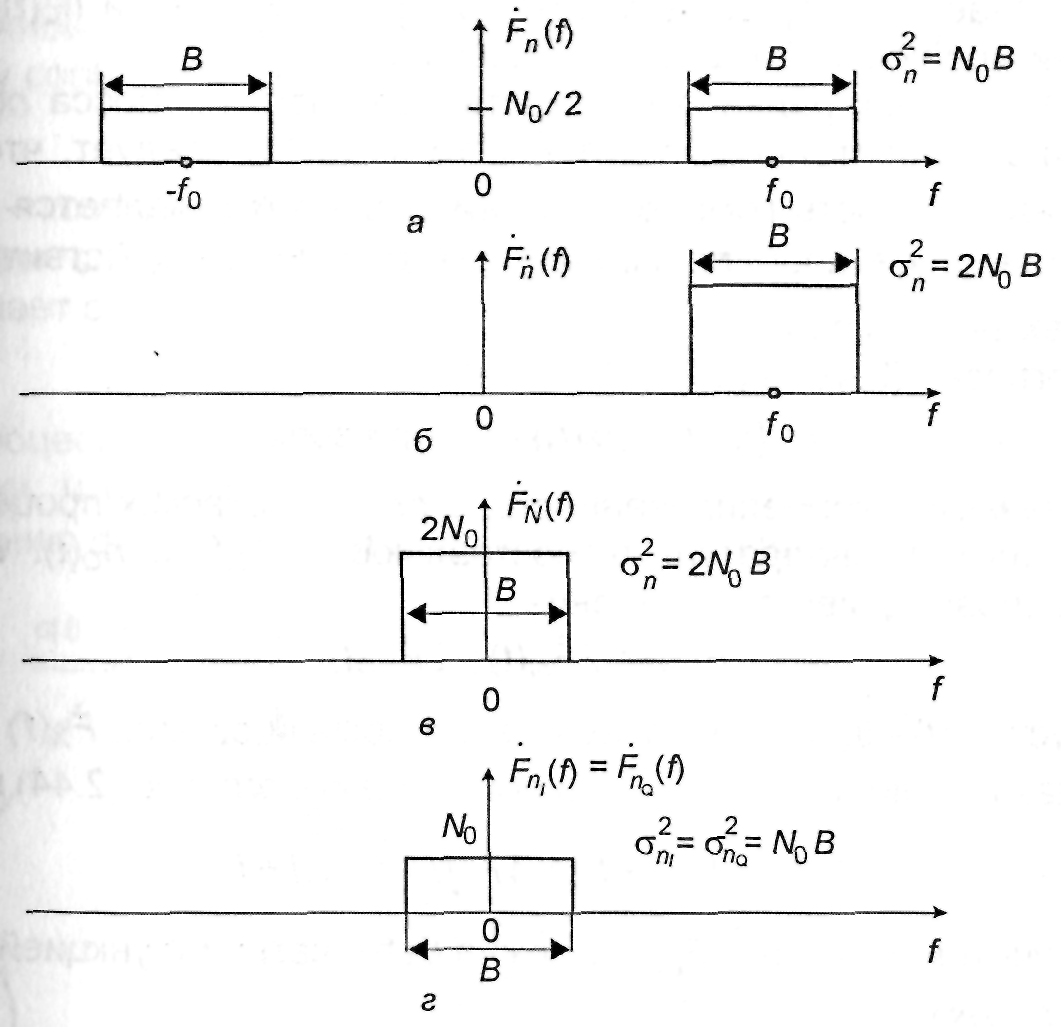
Рис. 2.3. Представление спектральных плотностей узкополосного процесса типа белого шума n(t): a – спектральная плотность исходного процесса n(t); б – спектральная плотность комплексного процесса ; в – спектральная плотность комплексной огибающей ; г – спектральная плотность квадратурных составляющих n_I(t) и n_Q(t)

, (2.48)

Таким образом,

, (2.49)

Из представленных результатов вытекают следующие выводы:

1.Так как есть действительная величина, то из (2.49) следует, что

, (2.50)

Это означает, что для любого момента времени t процессы n_I(t) и n_Q(t) являются некоррелированными, а в случае гауссовского случайного процесса и статистически независимыми.

2. Из выражений (2.44), (2.45), (2.48), (2.49) следует, что

, (2.51)

, (2.52)

Это означает, что средние мощности процессов n_I(t) и n_Q(t) равны средней мощности исходного процесса n(t).

3. Если спектральная плотность исходного процесса n(t) симметрична относительно частоты f₀, то из (2.46) следует, что спектральная плотность комплексной огибающей является четной функцией, а ее корреляционная функция действительной при всех значениях .

Согласно (2.49) и (2.50)

, (2.53)

что означает некоррелированность, а для гауссовских процессов и независимость квадратурных составляющих n_I(t) и n_Q(t). В этом случае справедливо соотношение

, (2.54)

Пусть х(t) – действительный узкополосный сигнал, – спектральная плотность комплексной огибающей. Согласно (2.44) и (2.46)

,

С учетом того, что должна быть четной функцией частоты, получаем

, (2.55)

Выражение (2.55) позволяет определить спектральную плотность действительного сигнала по известной спектральной плотности его комплексной огибающей.