5.5.3. Включение цепи с резистором и конденсатором на синусоидальное напряжение

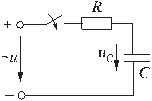
Пусть напряжение источника изменяется по закону

u = U_m sin(ωt + ψ).

Установившаяся составляющая напряжения на конденсаторе (см. рис. 5.11) равна:

u_Cу = -U_m X_C / Z sin(ωt + ψ – φ – π / 2). где: - полное сопротивление цепи; X_C = 1 / (ωC) – емкостное сопротивление; φ = -arctg(X_C / R) – угол сдвига фаз между установившимся током в цепи и приложенным синусоидальным напряжением.

Свободная составляющая напряжения на конденсаторе

u_Cсв = A e^-t/τ, τ = RC.

Переходное напряжение на конденсаторе

.

Полагая, что u_C(0_-) = 0, для постоянной интегрирования получим

.

Окончательно напряжение на конденсаторе можно записать в виде

.

Ток в цепи

.

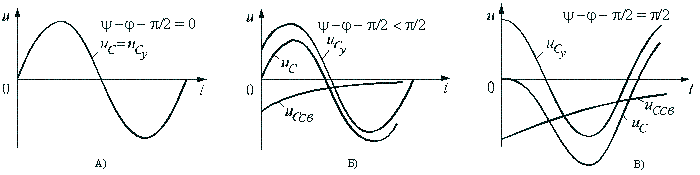
Зависимости переходного напряжения на конденсаторе от времени при различных значениях разностей ψ - φ показаны на рис. 5.12. Их анализ позволяет сделать следующие выводы.

Если в момент включения мгновенное значение установившегося напряжение на конденсаторе равно нулю (ψ – φ – π / 2 = 0), то и свободная составляющая напряжения равна нулю. В цепи сразу устанавливается режим (рис. 5.12 а).

Если в момент включения мгновенное значение установившегося напряжение на конденсаторе имеет наибольшее значение (ψ – φ – π / 2 = π / 2), то переходное напряжение достигает максимального значения приблизительно через половину периода и может приблизиться к удвоенной амплитуде установившегося напряжения, но не превысит его (рис. 5.12 в).

11. Переходные процессы в цепи с последовательным соединением r, l и c.

Рассмотрим процессы установления при включении источника постоянного напряжения на вход последовательной RLC- цепи (рис. 1.24).

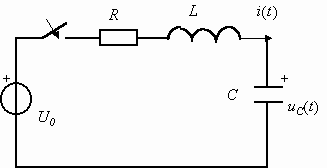
В данном случае электрическая цепь после коммутации содержит два реактивных элемента - индуктивность и емкость. Это означает, что дифференциальное уравнение цепи должно иметь второй порядок и поэтому должны быть определены два независимых начальных условия. Очевидно, что до коммутации цепь находилась в состоянии покоя, что соответствует нулевым начальным условиям: u_C(0₊) = u_C(0_-) = 0; i(0₊) = i(0_-) = 0.

Согласно второму закону Кирхгофа для цепи после коммутации справедливо следующее уравнение:

u_R(t) + u_L(t) + u_C(t) = U₀ ;

(1.24)

Будем интересоваться напряжением на емкости u_C(t) и поэтому другие напряжения, входящие в (1.24), а именно, напряжение на резисторе u_R(t) и напряжение на индуктивности u_L(t) выразим через u_C(t):

(1.25)

После подстановки (1.25) в (1.24) получим дифференциальное уравнение:

(1.26)

Полученное уравнение является линейным дифференциальным неоднородным уравнением второго порядка с постоянными коэффициентами. Его решение будем искать в виде: u_C(t) = u_Cсв(t) + u_Cвын.

Для определения свободной составляющей записываем соответствующее характеристическое уравнение LCp² + Rcp + 1 = 0 и определяем его корни:

(1.27)

где введены следующие обозначения: a = R / 2L - коэффициент затухания; w ₀ = 1/ Ö LC - резонансная частота контура. Далее записываем выражение для свободной составляющей

.

Вынужденную составляющую решения определим как установившееся значение напряжения на емкости в режиме постоянного тока в цепи после коммутации (рис. 1.25).

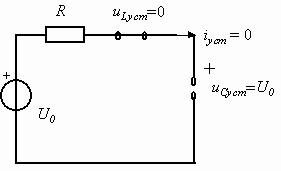
Из уравнения по второму закону Кирхгофа получим u_Cуст = u_Cвын = U₀. Таким образом, полное решение для напряжения

(1.28)

и для тока

. (1.29)

Выражение для тока необходимо для определения постоянных интегрирования. Используя нулевые начальные условия, из (1.28) и (1.29) при t = 0 получим: u_C(0₊)= A₁ + A₂ + U₀ = 0; i(0₊) = CA₁p₁ + CA₂p₂ = 0. Решение этой системы уравнений дает выражения для постоянных интегрирования:

. (1.30)

Дальнейшая конкретизация решения связана с видом корней р₁ и р₂ характеристического уравнения. В зависимости от соотношения между параметрами цепи возможны следующие виды корней (1.27):

a > w ₀ - корни вещественные, отрицательные, неравные, что соответствует, как будет показано ниже, апериодическому режиму переходных процессов;

a = w ₀ - корни вещественные отрицательные, равные. Режим называется критическим.

a < w ₀ - корни комплексные сопряженные с отрицательной вещественной частью, что соответствует колебательному режиму;

 

Далее рассмотрим эти три случая отдельно.

Апериодический режим. Условие a > w ₀ , как нетрудно убедиться, эквивалентно соотношениям: R > 2r и Q < 0.5, где r = Ö L / C - характеристическое сопротивление контура, а Q = r / R - его добротность. Таким образом, в рассматриваемом случае контур имеет значительные потери, т.е. является низкодобротным.

При этом корни (1.27) p_1,2 = - a ± b , где b = < a , являются вещественными отрицательными числами. Подставляя эти корни в (1.29) и (1.30), получим решение для функции напряжения на емкости:

(1.31)

Качественный график полученной функции показан на рис. 1.26. Переходное напряжение на емкости имеет апериодический ( неколебательный) характер и представляет из себя монотонно возрастающую функцию. Происходит апериодический заряд конденсатора до напряжения источника U₀ .

На этом же рисунке приведены качественные графики тока i(t) и напряжения на индуктивности u_L(t), при построении которых принималось во внимание то, что в цепи апериодический режим переходных процессов, а также соотношения, связывающие указанные функции с найденной функцией u_С(t). Начальные значения i(0₊)=0 и u_L(0₊)= U₀ , что следует из нулевых независимых начальных условий и уравнения Кирхгофа (1.24) для момента времени t=0₊: Ri(0₊) + u_L(0₊) + u_C(0₊) = u_L(0₊) = U₀ . Конечные или установившиеся значения, согласно рис. 1.25, равны i_уст = 0; u_Lуст = 0. Поскольку напряжение на индуктивности пропорционально производной от тока, то оно должно быть положительным во время возрастания тока и отрицательным во время его убывания.

Критический режим. Если a =w ₀ , то R = 2r и Q = 0,5. При этом корни (1.27) характеристического уравнения р₁ = р₂ = - a т.е. вещественные, отрицательные, равные. Рассматриваемый случай можно свести к апериодическому режиму и рассмотреть решение (1.31) при b =0 . При этом получается неопределенность, раскрывая которую по правилу Лопиталя, получим

В решении появляется характерный для случая кратных корней множитель t перед экспонентой. Качественно характер переходных процессов в критическом режиме не отличается от апериодического режима.

Колебательный режим. При выполнении условия a < w ₀ или R < 2r и Q > 0,5 корни (1.27) характеристического уравнения будут комплексными p_1,2 =- a ± j = - a ± jw _k , где w _k = - угловая частота свободных затухающих колебаний. При подстановке этих корней в (1.29) и (1.30) получим

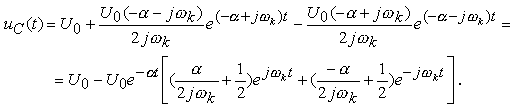
Далее, используя формулы Эйлера для экспонент с мнимыми показателями, окончательно найдем

u_C(t) = U₀ - U₀ e- a ^t [(a / w _k) sinw _kt +cosw _kt].(1.32)

При малых потерях в контуре (R < 2r ) переходный процесс имеет характер затухающих гармонических колебаний. Степень затухания зависит от показателя экспоненты a = R / 2L, который называется коэффициентом затухания. Период затухающих колебаний T_k определяется круговой частотой w _k и равен . На практике степень затухания колебаний часто оценивают декрементом затухания D , который определяет уменьшение амплитуды свободных колебаний за время периода. Из (1.32) следует, что

.

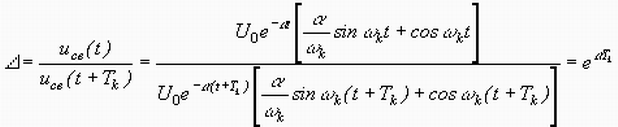Для оценки степени затухания используется также логарифмический декремент затухания ln  = a T_k.

Для самостоятельной работы рекомендуется изобразить качественные графики других напряжений в последовательном контуре при колебательном режиме переходных процессов.