0.Понятие матриц, виды матриц, примеры.

Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество п столбцов. Числа т и п называются порядками матрицы. В случае, если т = п, матрица называется квадратной, а число m = n -- ее порядком. Числа a ij , входящие в состав данной матрицы, называются ее элементами. В записи a ij первый индекс і означает номер строки, а второй индекс j -- номер столбца. В общем виде матрицу размером m×n записывают так

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы.Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. Различаются также матрицы, имеющие только одну строку или один столбец. Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом. Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Главной диагональю

квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол. Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей. Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей.

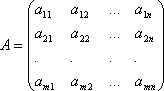
2. Умножение матрицы на число. Сложение матриц. Cвойства, примеры.

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы А на число k.

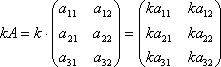
- Cв-ва.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

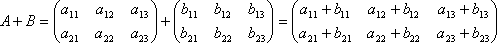
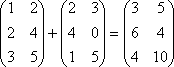
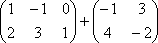- размеры разл.

Сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).

1.Умножение матриц

2 Матр а и в соглас-е, если число строк матр а равно числу столбцов матр в, и наоборот.

Оп-ция умн-я матриц определена только для соглас. матриц.

Кв матрицы одного и того же порядка и одной и той же размерности всегда согласованны.

Пусть задана матр А=aik i=1,m; k=1,n и матр В=bkj k=1,m; j=1,n. Тогда произв-ем А на В наз. матр С такая, что сik=ai1·b1k+ ai2·b2k +…+ ain·bnk, где i=1,m; k=1,n, т.е. эл-т i-той строки и k-того столбца матрицы произв-ия С равен ∑ произв-ий эл-ов i-той строки матр А на соответствующие эл-ты k-того столбца матр В.

Если выполняется равенство АВ=ВА, то матрицы А и В наз. перестановочными (коммутирующими)

Матр,получ. из данной заменой кажд ее строки столбц с тем же номером,наз. транспон-ой к данной.

Св-ва умножения:

1.А·(ВС)=(АВ)С

2. А(В+С)=АВ+ВС

3. (А+В)С=АС+ВС

4. α(АВ)=(αА)В

Св-ва транспонирования:

1.(А+В)^т=А^т+В^т

2. (АВ)^т=В·А^т

3. (А^т) ^т= А

Квадратная матрица А, которая не меняется при транспонировании, - симметричная.

Если матрица симметрична, то эл-ты, равноудаленные от главной диагонали, совпадают.

А= 2 5 -2

5 -7 3

-2 3 1