41. Два правила нахождения направления кориолисова ускорения.

Чтобы определить направление поворотного ускорения  , нужно мысленно перенести вектор   в точку М и руководствоваться правилом векторной алгебры. Согласно этому правилу, вектор   нужно направлять перпендикуляр­но к плоскости, определяемой векторами    и  , и так, чтобы, смотря с конца вектора  , наблюдатель мог видеть кратчайший поворот от   к   происходящим против движения часовой стрелки (рис. 30).

Для определения направления   можно также пользоваться следующим правилом Н. Е. Жу­ковского: чтобы получить направление поворот­ного ускорения  , достаточно составляющую   относительной скорости   точки М, перпенди­кулярную к вектору  ,  повернуть (в плоскости, перпендикулярной к вектору  ) на прямой угол вокруг точки М в направлении переносного вра­щения (рис.51).

 

Пример 14. Пусть тело вращается вокруг неподвижной оси z. По поверхности его движется точка М (рис. 52). Конечно, скорость этого движения точки – относительная скорость  , а скорость  вращения тела – угловая скорость переносного движения  .

Ускорение Кориолиса  , направлено перпен­дикулярно этим двум векторам, по правилу направления вектора век­торного произведения. Так, как пока­зано на рис. 52.

Рис.52

 

Нетрудно сформулировать более удобное правило определения  направ­ления вектора  :  нужно спроектировать вектор относитель­ной ско­рости   на плоскость перпендикуляр­ную оси переносного вращения и за­тем повер­нуть эту проекцию на 90 градусов в плоскости по направлению переносного вращения. Конечное положение проекции вектора    укажет направлениекориолисова ускорения. (Это правило было предложено Н.Е. Жуковским).

42.В пдф файле в телефоне)

43. Плоское движение твердого тела. Уравнение плоского движения. Кинематическая модель, задание движения и основное свойство плоского движения.

Изучение плоского движения начнем с построения кинематической модели твердого тела в плоском движении и определения числа степеней свободы тела.

Кинематическая модель, число степеней свободы тела.

П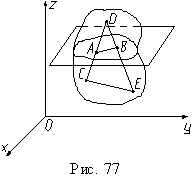 усть три точки C, D, E кинематической модели и, соответственно, все точки твердого тела, двигаются параллельно плоскости xOy системы координат Oxyz, которую мы принимаем за неподвижную. Тогда аппликаты точек тела будут постоянными, а изменяться будут только абсциссы и ординаты точек. Следовательно, нам нужно изучать в осях Oxy движение любого сечения тела плоскостью, параллельной координатной плоскостиxOy. В сечении получается отрезок прямой AB, который образуется от пересечения плоскости треугольника CDE данной плоскостью (рис. 77).

Т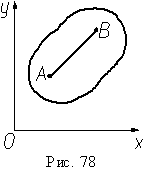 аким образом, при плоском движении твердого тела исследуется движение одного сечения тела в системе координатOxy, а кинематической моделью тела в плоском движении является отрезок прямой AB, лежащий в этом сечении (рис. 78). В сечении тела плоскостью Q получается плоская фигура (рис. 77), поэтому сечение часто называют плоской фигурой.

Зная кинематическую модель, определим число степеней свободы тела в плоском движении. Положение двух точек A иB кинематической модели определяется четырьмя параметрами x_A, y_A, x_B, y_B, которые связаны между собой уравнением постоянства расстояния AB: (x_B - x_A)² + (y_B - y_A)² = (AB)². То есть из четырех параметров независимых только три и тело в плоском движении имеет три степени свободы.