3.7. Полнота характеристик

Пусть оператор преобразования входного воздействия объекта или системы управления в выходную переменную представлен в форме дифференциального уравнения n-го порядка (3.1) или в форме передаточной функции (3.3).

Рассмотрим формулу (3.23) для реакции системы на воздействие при нулевых предначальных условиях. Если имеет место условие

,

где  — корень характеристического полинома

,

то коэффициент при экспоненте равняется нулю при любом воздействии. По реакциям такой системы нельзя полностью выявить ее собственные свойства такой системы — в реакциях будет отсутствовать составляющая (мода), соответствующая корню .

Говорят, что по рассматриваемой паре вход-выход система оказывается неполной. Временные характеристики — реакции на типовые воздействия при нулевых начальных условиях — не отражают полностью собственных свойств системы по неполной паре вход-выход.

Операторные полиномы A и B дифференциального уравнения (3.2) неполной системы имеют нетривиальный общий делитель , а передаточная функция (3.3) имеет диполь . Если полиномы A и B не являются взаимно простыми, то передаточную функцию называют вырожденной.

Годографы вырожденных передаточных функций

построенные при изменении аргумента s вдоль некоторого контура C на комплексной плоскости, в частности, вдоль мнимой оси т. е. частотные характеристики также отражают только полную часть системы.

Потеря части собственных свойств систем особенно существенна, если  — правый корень. Сокращение вырожденной передаточной функции не рекомендуется. В случае правого полюса сокращение просто недопустимо. При ненулевых начальных условиях, например, вызванных воздействиями, приложенными к другим входам системы, появляются свободные движения. Если эти начальные условия таковы, что

,

то, как следует из (3.24), свободные движения содержат моду .

Свойство полноты относится к модели типа  — системы со связями со средой — это свойство конкретной передачи.

Если даны операторные полиномы и или полиномы знаменателя и числителя передаточной функции объекта или системы управления по выбранной паре вход-выход, наличие общих делителей или диполей можно выявить несколькими способами [ ].

Во-первых, можно непосредственно сопоставить корни полиномов A и B. Это наилучший способ, здесь выявляются и приближенные диполи передаточных функций. Во-вторых, выявить наибольший общий делитель полиномов делением их по алгоритму Евклида. В-третьих, можно исследовать результант полиномов — специальный определитель порядка , построенный из коэффициентов полиномов A и B. Полиномы имеют по меньшей мере один общий корень, если их результант равен нулю.

Свойство полноты одномерной системы непосредственно связано со свойствами управляемости и наблюдаемости, которые определяются и для многомерных систем.

3.8. Характеристики типовых звеньев

Систему можно представить в виде соединения типовых динамических звеньев. Для реализации любой передаточной функции в виде правильной дроби достаточно двух типов звеньев: интеграторов и усилителей. Действительно, если представить модель вход-выход в форме пространства состояний (3.7), то можно только с помощью операций интегрирования, умножения на постоянные коэффициенты и суммирования реализовать передаточную функцию в виде правильной дроби.

Если степень числителя передаточной функции превышает степень знаменателя, то необходимо звено дифференцирующего типа.

В теории управления состав типовых звеньев несколько расширен исходя из соображения удобства — необходимы звенья, моделирующие часто встречающиеся элементы, а также позволяющие представить передаточные функции общего вида в виде произведения или суммы простейших передаточных функций, иначе говоря, последовательным и параллельным соединением типовых звеньев. Число таких звеньев невелико и определяется типом нулей и полюсов передаточной функции.

В классической теории автоматического регулирования изучению свойств типовых звеньев уделяется большое значение. Рассмотрим основные характеристики некоторых типов звеньев.

1. Усилительное (пропорциональное, безынерционное) звено описывается так

.

Передаточная функция звена имеет вид

.

Функция веса представляет собой импульс с измененной площадью, а переходная характеристика усилительного звена — ступенчатая функция высоты . Амплитудно-частотная характеристика , т. е. усиление звена не зависит от частоты; идеальное усилительное звено также не вносит фазовых сдвигов .

2. Интегрирующее звено

описывается дифференциальным уравнением первого порядка

,

а его передаточная функция равна

.

Временные характеристики интегрирующего звена описываются следующими выражениями:

,

т. е. реакция интегратора на идеальный импульс представляет собой ступенчатую функцию, а реакция на ступенчатую функцию — линейная функция для (рис. 3.9, а).

Комплексная частотная характеристика интегратора выражается так

,

следовательно, АФХ интегрирующего звена совпадает с отрицательной полуосью мнимых. Амплитудно-частотная характеристика интегратора

показывает, что с повышением частоты усиление звена падает. При уменьшении частоты входного сигнала усиление растет до бесконечности при нулевой частоте, отвечающей постоянному сигналу. Действительно, реакция интегратора на ненулевой постоянный сигнал линейно растет или убывает в зависимости от знака, т. е. в пределе амплитуда реакции стремится к бесконечности. Интегрирующее звено на всех частотах (кроме нулевой частоты) вносит отрицательный фазовый сдвиг, равный

рад = .

Логарифмическая амплитудно-частотная характеристика интегратора

представляет собой прямую с наклоном -20 дБ/дек, пересекающую ось частот при (см. рис. 3.9, б).

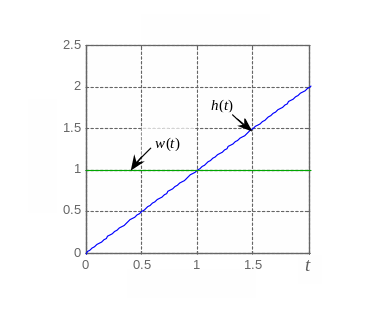
а б

Рис. 3.9. Харктеристики интегрирующего звена: временные (а); ЛЧХ (б)

3. Апериодическое звено первого порядка (инерционное звено) имеет передаточную функцию вида

,

где: k — коэффициент усиления; T — постоянная времени. Дифференциальное уравнение инерционного звена записывается так

.

На рис. 3.10, а изображены временные характеристики звена и , а на рис. 3.10, б — его амплитудно-фазовая характеристика — годограф вектора для значений частот от до . Годограф Найквиста представляет собой окружность с центром в точке . Обычно АФХ строят для неотрицательных значений частот. Тогда годограф при начинается на действительной полуоси в точке и заканчивается при бесконечной частоте в начале координат.

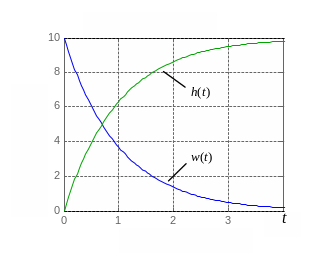
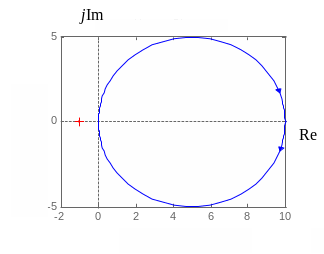
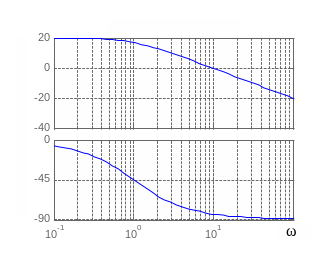
Рис. 3.10. Харктеристики инерционного звена: временные (а); амплитудно-фазовая (б); ЛЧХ (в)

Логарифмические частотные характеристики инерционного звена первого порядка

;

представлены на рис. 3.10, в. Видно, что ЛАЧХ имеет низкочастотную и высокочастотную асимптоты

которые с приемлемой для практических расчетов точностью аппроксимируют ЛАЧХ этого звена. Максимальное отличие между точной и асимптотической характеристиками на частоте равно -3 дБ. Фазочастотная характеристика звена также имеет асимптоты:

.

4. Звенья второго порядка имеют передаточную функцию следующего вида

,

где  — коэффициент демпфирования. Дифференциальное уравнение звеньев второго порядка запишется так

.

При имеем апериодическое звено второго порядка; значения дают колебательное звено; при получается консервативное звено. Конкретный тип звена определяется полюсами передаточной функции: апериодическое звено второго порядка имеет действительные отрицательные полюсы; у колебательного звена полюсы комплексные в левой полуплоскости; консервативное звено имеет мнимые полюсы.

На рис. 3.11, а изображены переходные характеристики звеньев второго порядка для различных значений коэффициента демпфирования. Логарифмические частотные характеристики звеньев с различными значениями = 0.02; 0.1; 0.707; 2.0 изображены на рис. 3.11, б.

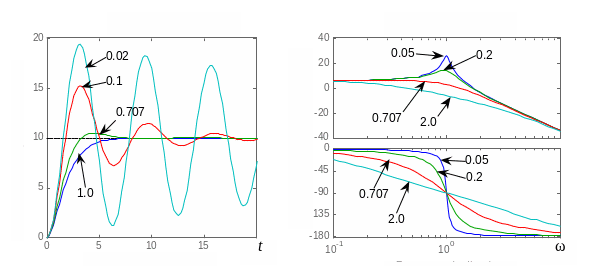
Рис. 3.11. Характеристики звеньев второго порядка при различных значениях коэффициента демпфирования: переходные харктеристики (а); ЛЧХ (б)

5. Пропорционально-дифференцирующее звено описывается передаточной функцией

,

которой соответствует дифференциальное уравнение

.

Частотные характеристики этого звена были приведены на рис. 3.7.

Иногда используют и некоторые другие типы звеньев.