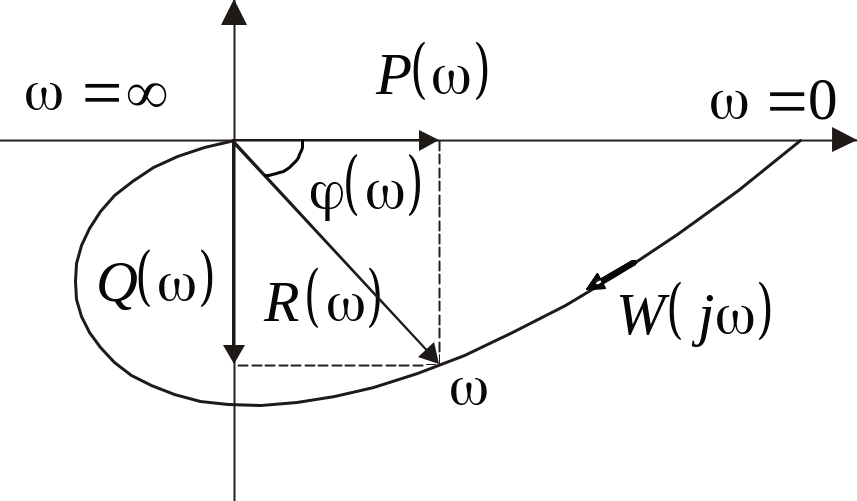3.1.3. Временные характеристики

Временные характеристики являются одной из форм представления операторов преобразования переменной f(t) в переменную y(t).

Импульсная переходная функция или функция веса w(t) — реакция системы на единичный идеальный импульс (t) при нулевых начальных условиях. Если известна функция веса, то переменная выхода определяется как интеграл свертки

.

На рис. 3.2, а приведены примеры функций веса двух систем.

Графики функций веса наглядно показывают такое понятие, как память динамического элемента — степень влияния предыстории на переменную выхода в последующие моменты времени (инерционные свойства элемента). Практическая “ширина” функции веса количественно оценивает длительность памяти фильтра. Память короткая, если ширина функции веса мала (кривая 1 на рис. 3.2, а), и длинная, если функция веса занимает большой интервал времени (кривая 2 на рис. 3.2, а).

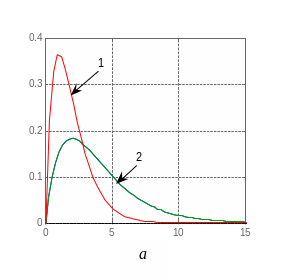
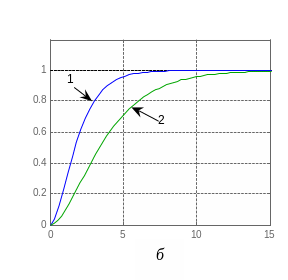
Рис. 3.2. Временные характеристики: а — функции веса; б — переходные характеристики

Другая временная характеристика — переходная характеристика h(t) — реакция системы на единичную ступенчатую функцию 1(t) при нулевых начальных условиях. На рис. 3.2, б приведены примеры переходных характеристик двух систем, менее инерционной (кривая 1) и более инерционной (кривая 2).

Для автономных систем не подходят приведенные ранее определения временных характеристик. Вместе с тем, можно рассматривать свободные движения при типовых начальных условиях; обычно принимают: .

3.1.4. Частотные характеристики

Частотные характеристики представляют собой зависимости амплитуды и фазы установившихся реакций систем на гармонические сигналы различных частот. Установившиеся реакции устойчивых линейных систем на гармонические сигналы имеют вид гармонических сигналов той же частоты, однако их амплитуда и фаза в общем случае зависят от частоты.

На рис. 3.3 изображены графики гармонического сигнала, амплитуда и круговая частота которой равны единице 1(t), и реакции системы на такой сигнал. Можно заметить, что переходный процесс практически затухает за один период колебаний. Амплитуда установившейся реакции меньше единицы, т. е. при прохождении через систему сигнал ослабляется. Видно, что реакция запаздывает — временной сдвиг равен с; отрицательный фазовый сдвиг получится умножением временного сдвига на частоту сигнала рад . Такая ситуация характерна для систем, обладающих инерционными свойствами (памятью).

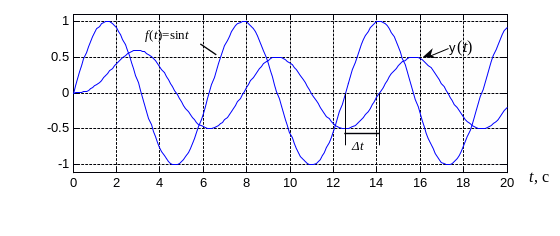
Рис. 3.3. Пример реакции системы на гармонический сигнал

Комплексная частотная характеристика W(j) дает возможность определить амплитуду R() и фазу () гармонического сигнала на выходе системы по значению частоты:

(3.6)

где R() = modW(j) и () = argW(j) — амплитудная и фазовая частотные характеристики (АЧХ и ФЧХ), а P() = ReW(j) и Q() = ImW(j) — вещественная и мнимая частотные характеристики.

На рис. 3.4 изображен примерный вид годографа W(j), называемого амплитудно-фазовой характеристикой. Длина вектора на конкретной частоте равна отношению амплитуд выхода и входа, иначе, амплитуде реакции при единичной амплитуде входного гармонического сигнала. Реальные объекты и системы с повышением частоты хуже пропускают сигналы — ослабляют амплитуду и вносят отрицательный фазовый сдвиг, что и иллюстрируется на этом примере.

	Рис. 3.4. Пример амплитудно-фазовой характеристики

Амплитудно-фазовая характеристика (АФХ), называемая также диаграммой Найквиста (H. Nyquist), в одной кривой объединяет сведения об амплитудной и фазовой частотных характеристиках.

Вид АФХ дает наглядный комплексный образ системы в частотной области. В целях количественного анализа динамики объектов и расчетов регуляторов рекомендуется выбрать на АФХ достаточно большое число точек с отметками частоты. Это возможно, если изучают и формируют свойства систем на сравнительно узких диапазонах частот. Примерами являются объекты теплоэнергетики и технологические процессы. Недостатком АФХ является то, что одна и та же абсолютная ошибка ее построения дает большие относительные ошибки на высоких частотах, где усиление мало.

Особенностью частотных характеристик является то, что каждая их точка несет вполне определенную информацию о системе. Это выгодно отличает частотные характеристики от временных характеристик, у которых отдельно взятая точка в общем случае не несет никакой информации о системе.

Для автономных систем, вообще говоря, не определены понятия частотных характеристик. Вместе с тем, для структурированных моделей, содержащих контуры, частотные характеристики имеют смысл и весьма информативны при оценке роли контуров на различных частотах.