3.5. Построение временных характеристик

Временные характеристики — импульсная переходная функция w(t) и переходная характеристика h(t) — могут быть получены экспериментально, если удается подать на вход устойчивого объекта воздействие в виде достаточно узкого импульса с необходимой амплитудой или ступенчатой функции времени. Последнее более реально; функцию веса w(t) впоследствии можно получать дифференцированием функции h(t).

Статистические методы непараметрической идентификации [ ] позволяют оценивать ординаты функции веса w(t) путем обработки данных вход-выход объекта в виде случайных сигналов, быть может, имеющих место в режиме нормальной эксплуатации (корреляционный анализ).

Существуют методы построения временных характеристик по частотным, базирующиеся на обратном преобразовании Фурье (I. Fourier).

3.5.1. Построение временных характеристик по дифференциальным уравнениям

В том случае, когда исходная информация об объекте представлена в форме дифференциального уравнения (3.1), временные характеристики получают его решением.

В классической теории автоматического регулирования для решения дифференциальных уравнений привлекают так называемый операторный метод, теоретической основой которого является преобразование Лапласа. Метод особенно удобен в случае типовых воздействий в виде обобщенных функций и позволяет легко учесть ненулевые начальные условия.

Пусть дано дифференциальное уравнение n-го порядка звена или системы автоматического управления

Необходимо получить выражения для импульсной переходной функции (функции веса) , переходной характеристики h(t), а также для реакции в случае воздействия общего вида. Пусть изображение по Лапласу воздействия на входе системы или звена представляет собой рациональную функцию от s

Если преобразовать по Лапласу дифференциальное уравнение n-го порядка, то после разрешения полученного алгебраического уравнения относительно изображения переменной выхода имеем

(3.17)

Здесь полином определяется начальными (точнее, предначальными) условиями. Необходимость различать посленачальные и предначальные условия обусловлена тем, что при подаче воздействий на вход системы ее состояние в начальный момент времени может изменяться скачком.

Если начальные условия нулевые, то изображение выхода равно:

где W(s) — передаточная функция.

Искомое решение — переменная на выходе системы (оригинал) — получается обратным преобразованием Лапласа

(3.18)

где c — абсцисса сходимости. Формула обращения Римана–Меллина (D.Riemann ― H. Mellin) (3.18) устанавливает однозначное соответствие между оригиналом и изображением в точках непрерывности оригинала. Имеются алгоритмы и программы, позволяющие вычислять интеграл (3.18) при произвольных функциях Y(s).

Практическое вычисление оригинала y(t) удобно производить, основываясь на теореме о вычетах, согласно которой значение интеграла (3.18) может быть представлено суммой вычетов подынтегральной функции

где  — вычет функции в полюсе  — число полюсов изображения . При t < 0 функция y(t) = 0.

В случае обыкновенных линейных дифференциальных уравнений и типовых воздействий изображение является дробно-рациональной функцией, которую можно представить в виде суммы простейших дробей

(3.19)

где  — производная полинома по s;  — простые полюсы;

Оригинал y(t) в соответствии с разложением (3.19) имеет вид

Импульсная переходная функция (функция веса) представляет собой реакцию системы на -функцию при нулевых начальных условиях. Поскольку изображение -функции

то функция веса представляет собой обращение по Лапласу передаточной функции

И наоборот, передаточная функция является изображением функции веса.

Разложение передаточной функции на сумму простейших дробей в случае простых полюсов имеет вид

(3.20)

где  — коэффициенты разложения (вычеты):

(3.21)

Пример 2. Найдем с помощью формул (3.10) и (3.11) выражение для функции веса по передаточной функции

(3.22)

Полюсы передаточной функции . Разложение (3.12) на сумму простейших дробей имеет вид

Обратное преобразование Лапласа дает

Переходная характеристика h(t) представляет собой реакцию системы на единичную ступенчатую функцию 1(t) при нулевых начальных условиях.

Поскольку

то

Полюсами изображения являются полюс воздействия 0 и полюсы передаточной функции. Легко убедиться, что

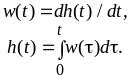
Пример 3. Получим выражение для переходной характеристики системы с передаточной функцией (3.22). Разложение изображения на сумму простейших дробей дает

где

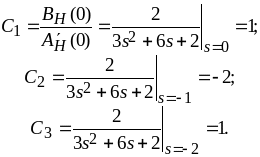
Следовательно, переходная характеристика описывается функцией:

В общем случае произвольного воздействия разложение изображения переменной выхода (3.7) запишется как

.

(3.23)

Здесь  — полюсы передаточной функции  — полюсы изображения воздействия . Принято, что , т.е. полюсы воздействия не равны полюсам передаточной функции (нет обобщенного резонанса).

В выражении (3.23) первая группа слагаемых определяет переходную составляющую вынужденного движения ; вторая группа — установившаяся составляющая вынужденного движения y_уст(t) а третья — свободные движения

.

Установившееся вынужденное движение обусловлено полюсами изображения воздействия ; переходная составляющая вынужденного движения образуется из-за ненулевых посленачальных условий (изменение начальных условий приложением в момент времени t = 0 конкретного воздействия) и определяется полюсами передаточной функции; свободные движения имеют место при ненулевых предначальных условиях и также определяются полюсами передаточной функции.

Автономная система управления M_S , представленная в форме однородного дифференциального уравнения

,

имеет решение вида

.

(3.24)

Если изображение имеет кратные полюсы, то вместо формул (3.23), (3.24) записываются более сложные выражения [ ].
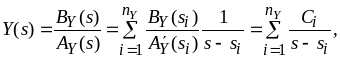
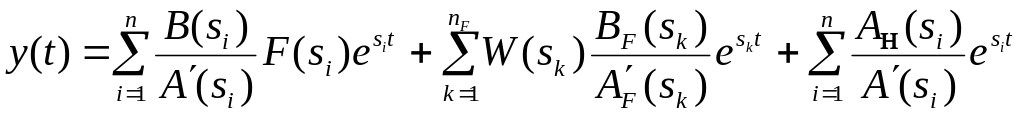