Часть 2. Теория линейных непрерывных систем управления

3. Линейные модели и характеристики систем управления

Рассмотрим различные формы представления конечномерных линейных непрерывных стационарных детерминированных моделей систем управления. Согласно предложенной в 2.4.2 систематизации, такие модели относятся к простейшему классу КSDL.

3.1. Модели вход-выход

Основными формами представления операторов преобразования входных переменных f(t) в переменные выхода y(t) являются: дифференциальные уравнения, передаточные функции, временные и частотные характеристики. Эти и некоторые другие представления операторов рассматриваемого класса моделей могут быть приняты за основу задания динамических свойств в терминах “вход-выход”. Для одномерных систем переменные f(t) и y(t) являются скалярами.

3.1.1. Дифференциальные уравнения

Обыкновенное линейное дифференциальное уравнение n-го порядка с постоянными коэффициентами обычно записывается так:

.

(3.1)

Если ввести оператор дифференцирования по времени , то уравнение (3.1) примет более компактную форму

(3.2)

где собственный операторный полином и операторный полином при воздействии имеют вид

; .

Автономные системы описываются однородными дифференциальными уравнениями

(3.3)

или в операторной форме

0.

Дифференциальные уравнения -го порядка (3.1), (3.2) дополняются начальными условиями

3.1.2. Передаточные функции

Передаточная функция равна отношению изображений по Лапласу переменных выхода и входа при нулевых начальных условиях

где интегральное преобразование Лапласа (P. Laplace) определяется так:

Преобразуя дифференциальное уравнение (3.1) при нулевых начальных условиях, получаем алгебраическое уравнение для изображений

Отсюда следует, что передаточная функция легко записывается по дифференциальному уравнению в операторной форме (3.2), путем замены символа оператора дифференцирования на комплексный аргумент

.

(3.4)

И наоборот, если известна передаточная функция системы, то немедленно записывается и дифференциальное уравнение.

Пример 1. Пусть система описывается дифференциальным уравнением второго порядка

или в операторной форме

.

Преобразуем уравнение по Лапласу. Воспользуемся при этом свойством линейности оператора преобразования L, а также теоремой о дифференцировании оригинала

Последнее уравнение перепишем в другом виде:

При нулевых начальных условиях отношение изображений, т. е. передаточная функция равна

Переход в область изображений переменных удобен тем, что по передаточной функции системы и изображению переменной входа легко найти изображение выхода

Свойство коммутативности приведенного выражения служит иллюстрацией единства и двойственности сигналов и систем. Действительно, последнее выражение, записанное в другом порядке

,

можно трактовать и так, что входная переменная с изображением преобразуется фильтром с передаточной функцией . В результате получается выходная переменная с тем же изображением (рис. 3.1).

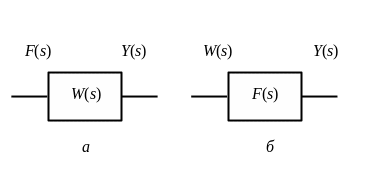
Рис. 3.1. Иллюстрация единства и дуальности сигнала и системы

Оператор, связывающий вход и выход системы, можно задать коэффициентом и множествами нулей (корней полинома числителя) , и полюсов (корней полинома знаменателя) , передаточной функции

(3.5)

В отличие от полиномиальной формы (3.3), эту форму задания передаточных функций иногда называют факторизованной.

Разложение передаточной функции на сумму простейших дробей в случае простых полюсов , имеет вид

.

Вводится понятие структуры оператора преобразования. Для дифференциального уравнения n-го порядка (3.1) и передаточной функции (3.4) задание структуры означает задание целых чисел — степеней и полиномов A и B.

Параметрами оператора являются коэффициенты полиномов.

Компактное кодирование информации о системе, представленной в форме дифференциального уравнения (3.1) или передаточной функции (3.4) сводится к указанию двух массивов — коэффициентов полиномов числителя и знаменателя .

Автономные системы (3.3) не имеют входа, поэтому для них понятие передаточной функции не определено. Вместе с тем, можно искусственно принять, что на вход автономной системы подана -функция, изображение по Лапласу которой равна единице. Тогда изображение выхода автономной системы является передаточной функцией того преобразователя, который из идеального импульса формирует адекватное воздействие среды. Такой прием также является примером использования дуальности сигналов и систем в случае линейных моделей.