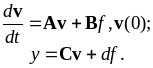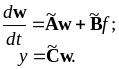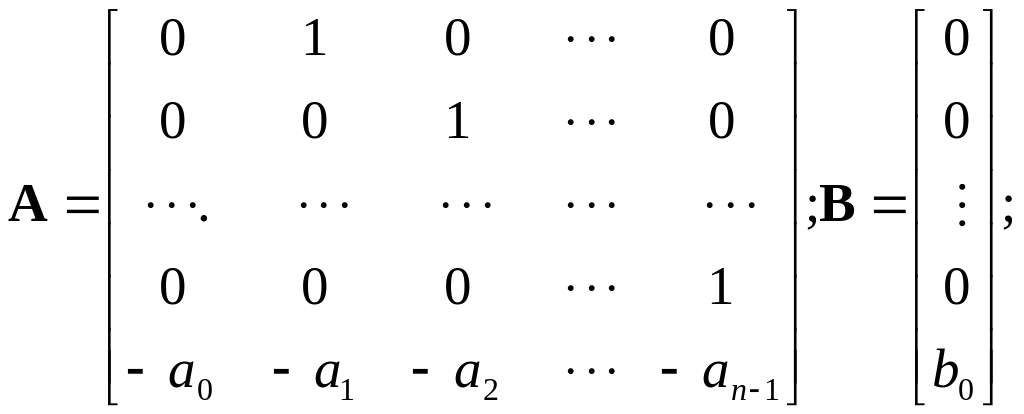3.4. Построение моделей вход-выход по уравнениям в форме пространства состояний

Пусть дифференциальные уравнения объекта или системы управления записаны в форме пространства состояний:

(3.8)

Для простоты принят одномерный случай: переменные входа f и выхода y являются скалярами; матрица входа B — столбец; матрица выхода C — строка; d — скаляр обхода.

3.4.1. Вычисление передаточной функции

Преобразуем уравнения (3.8) по Лапласу при нулевых начальных условиях:

(3.9)

Выразим решение системы алгебраических уравнений — изображение вектора состояний — в следующей форме:

(3.10)

где — матрица, обратная характеристической матрице матрицы A; I — единичная матрица. Подставим (3.10) в (3.9) и получим

Передаточная функция W может быть записана и иначе, если учесть, что

(3.11)

где — присоединенная матрица,

(3.12)

определитель характеристической матрицы — характеристический полином системы дифференциальных уравнений(3.7). С учетом (3.11) передаточная функция запишется как

(3.13)

Элементами присоединенной матрицы являются алгебраические дополнения элементов характеристической матрицы , т. е. полиномы. Их степени не могут превосходить (n - 1). Таким образом, как видно из формулы (3.13), степень m = deg B полинома числителя передаточной функции W не может быть выше степени n = deg характеристического полинома и равна ей только при d  0. Это ограничивает возможности описания динамических систем в нормальной форме пространства состояний (m  n).

Имея полиномы передаточной функции (3.13), легко записать дифференциальное уравнение n-го порядка. Остается решить вопрос с перечислением начальных условий. Рассмотрим случай d = 0, т.е. m < n. Как следует из уравнения выхода системы (2.28), начальное значение выхода определяется из вектора начального состояния путем умножения на матрицу выхода:

Продифференцируем уравнение выхода по времени

Следовательно, начальное значение производной выхода

Легко видеть, что

и т.д. Последнее из начальных условий для дифференциального уравнения n-го порядка определяется по формуле

Упорядочим начальные условия y(0),..., y^(n-1)(0) в вектор y(0). Тогда имеем

где V — так называемая матрица наблюдаемости:

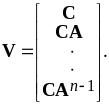
Если существует , т. е. det V  0, или ранг квадратной матрицы V равен ее размеру n, то можно записать зависимость начального (или текущего) состояния от значения выхода и его производных

3.4.2. Построение модели в форме пространства состояний по дифференциальному уравнению n-го порядка

Для одномерной системы легко записать матрицы канонических форм пространства состояний по дифференциальному уравнению го порядка или передаточной функции. Построение моделей вход-состояние-выход для многомерных объектов, описанных, например, передаточными матрицами, представляет более сложную задачу так называемой минимальной реализации [36].

Переход от одного дифференциального уравнения n-го порядка (3.1) к системе уравнений в форме пространства состояний (3.8) неоднозначен из-за произвола в выборе переменных состояний. Действительно, невырожденное преобразование вектора переменных состояния

(3.14)

где w — новый вектор состояния, не изменяет оператора преобразования вход-выход. Той же самой остается передаточная функция. Покажем это.

Подставляя (3.14) в (3.8), получим (при коэффициенте обхода d =0)

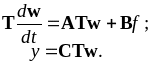
Поскольку матрица преобразования T невырожденная, то существует обратная матрица . С учетом этого

Введя новые обозначения получим

(3.15)

Покажем, что системе уравнений в нормальной форме (3.15) соответствует та же передаточная функция, что и системе (3.8). По формуле, полученной в предыдущем пункте, имеем

.

Выразим новые матрицы через старые и проведем преобразования

Чаще всего выбирают следующие связи между переменными состояния

Это сразу определяет первые n-1 уравнений состояния

Если m = 0, т. е. дифференциальное уравнение имеет вид:

.

Без потери общности примем ; тогда n-е уравнение состояния находитcя просто:

Здесь Матрицы нормальной формы в так называемом каноническом наблюдаемом базисе имеют вид:

(3.16)

Если оператор при воздействии B(p), т. е. полином числителя B передаточной функции W, имеет степень 0 <m  n, то вид матрицы-столбца изменится; она является решением следующей системы линейных уравнений:

,

где B — искомая матрица-столбец (вектор);

L — треугольная матрица коэффициентов

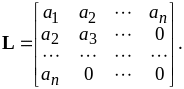
Очевидно, при таком выборе переменных состояния нет вопроса о вычислении начальных условий, так как

В ряде случаев удобен другой выбор переменных состояния, исключающий необходимость вычисления матрицы B. Матрица состояния A имеет ту же форму (3.16) — так называемую сопровождающую форму Фробениуса. Матрица входа B определяется так:

а матрица выхода равна

В этом — каноническом управляемом базисе выход y уже не является первой по номеру переменной состояния, а выражается как линейная комбинация переменных состояния. Это обусловливает необходимость перечисления начальных условий

Коэффициент обхода d отличен от нуля только при равенстве степеней m и n полиномов B и A:

До записи матриц нормальной формы при передаточную функцию рекомендуется представлять в виде суммы коэффициента обхода d и правильной дроби:

где m₁ = deg B₁ < n, а полином A имеет единичный старший коэффициент.