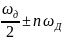- •Что понимается под задачей синтеза дискретного фильтра?
- •Может ли частотная характеристика дискретного фильтра в точности совпадать с частотной характеристикой аналогового прототипа? Почему?
- •Опишите процедуру синтеза дискретного фильтра по аналоговому прототипу методом билинейного z-преобразования.
- •Приведите формулу, описывающую трансформацию частотной оси при билинейном z‑преобразовании.
- •Накладывает ли метод билинейного z-преобразования какие-либо ограничения на тип ачх синтезируемых фильтров? Если да, то какие именно?
- •На каких частотах дискретный фильтр, синтезированный методом билинейного z‑преобразования, имеет такой же комплексный коэффициент передачи, как аналоговый прототип при частоте, равной нулю?
- •Опишите процедуру синтеза дискретного фильтра по аналоговому прототипу методом инвариантной импульсной характеристики
- •Накладывает ли метод инвариантной импульсной характеристики какие-либо ограничения на тип ачх синтезируемых фильтров? Если да, то какие именно?
- •Запишите общую формулу для целевой функции, используемой при прямом синтезе дискретных фильтров путем минимизации p-нормы ошибки.
- •Для чего при прямом оптимальном синтезе дискретных фильтров используются весовые функции?
- •При использовании каких форматов (с фиксированной или плавающей точкой) эффекты конечной точности представления чисел сказываются сильнее? Почему?
- •Какие предположения о статистических свойствах шума квантования обычно используются для его аналитического описания? При каких условиях они хорошо выполняются на практике?
- •В чем состоит сущность оптимального неравномерного квантования? в каких диапазонах уровни такого квантования оказываются расположены чаще, а в каких – реже?
- •Для каких фильтров — рекурсивных или нерекурсивных — ошибки квантования коэффициентов сказываются сильнее? Почему?
- •Дайте определение понятию «адаптивный фильтр».
- •Что такое «обучение с учителем» и «обучение без учителя»?
- •Почему адаптивные фильтры чаще всего строятся на основе нерекурсивных фильтров?
- •Может ли нерекурсивный адаптивный фильтр оказаться неустойчивым? Почему?
- •В чем состоит сущность lms-алгоритма?
- •Как используются адаптивные фильтры для реализации линейного предсказания? Приведите соответствующую структурную схему.
- •Как используются адаптивные фильтры для реализации подавления шума? Приведите соответствующую структурную схему.
- •Как используются адаптивные фильтры для выравнивания канала связи? Приведите соответствующую структурную схему. Какие два разных режима работы при этом могут иметь место?
- •В чем состоит идея полифазного представления сигналов?
Что понимается под задачей синтеза дискретного фильтра?
Под
синтезом дискретного фильтра понимается
выбор таких наборов коэффициентов
 ,
при которых характеристики проектируемого
фильтра удовлетворяют заданным
требованиям. Строго говоря в задачу
синтеза также входит и выбор подходящей
структуры фильтра с учётом конечной
точности вычислений.
,
при которых характеристики проектируемого
фильтра удовлетворяют заданным
требованиям. Строго говоря в задачу
синтеза также входит и выбор подходящей
структуры фильтра с учётом конечной
точности вычислений.
Может ли частотная характеристика дискретного фильтра в точности совпадать с частотной характеристикой аналогового прототипа? Почему?
Нет, не может. При синтезе ДФ по аналоговому прототипу необходимо преобразовать функцию передачи аналогового фильтра H(p) в функцию передачи ДФ H(z). Получившийся ДФ не может быть полностью идентичен аналоговому прототипу хотя бы потому, что частотные характеристики ДФ являются периодическими. Можно лишь говорить об определенном соответствии характеристик аналогового и дискретного фильтров.
Опишите процедуру синтеза дискретного фильтра по аналоговому прототипу методом билинейного z-преобразования.
Операторный
коэффициент передачи аналогового
фильтра представляет собой
дробно-рациональную функцию
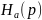 .
Для дискретного фильтра осуществляется
переход в z-область, функция передачи
ДФ
.
Для дискретного фильтра осуществляется
переход в z-область, функция передачи
ДФ
 также представляет собой дробно-рациональную
функцию(но по переменной z). Чтобы
частотные характеристики аналогового
и дискретного фильтров были связаны
простой зависимостью, искомая замена
переменной должна отображать мнимую
ось в p-области на единичную окружность
в z-области. Тогда частотные характеристики
аналогового и дискретного фильтров
будут связаны лишь трансформацией
частотной оси. Простейшей функцией,
удовлетворяющей этим требованиям,
является билинейное преобразование:
также представляет собой дробно-рациональную
функцию(но по переменной z). Чтобы
частотные характеристики аналогового
и дискретного фильтров были связаны
простой зависимостью, искомая замена
переменной должна отображать мнимую
ось в p-области на единичную окружность
в z-области. Тогда частотные характеристики
аналогового и дискретного фильтров
будут связаны лишь трансформацией
частотной оси. Простейшей функцией,
удовлетворяющей этим требованиям,
является билинейное преобразование:
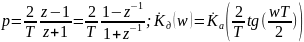
Приведите формулу, описывающую трансформацию частотной оси при билинейном z‑преобразовании.
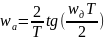 ,
где
,
где
 -
частота аналогового сигнала,
-
частота аналогового сигнала,
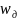 -
частота дискретизации.
-
частота дискретизации.
Накладывает ли метод билинейного z-преобразования какие-либо ограничения на тип ачх синтезируемых фильтров? Если да, то какие именно?
Да, накладывает. Исходя из типа АЧХ фильтра, необходимо учитывать следующее соответствие между частотными характеристиками аналогового и дискретного фильтров:
,
тогда если
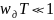 ,
то
,
то
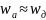 ,
поэтому в области НЧ частотные
характеристики аналогового и дискретного
фильтров почти совпадают. Далее, по мере
роста функции тангенса, ЧХ будет сильнее
сжиматься по горизонтали и на частоте
Найквиста примет значение, которое ЧХ
аналогового фильтра имела бы на
бесконечной частоте. Выше сказанное
проиллюстрируем на рисунке ниже:
,
поэтому в области НЧ частотные
характеристики аналогового и дискретного
фильтров почти совпадают. Далее, по мере
роста функции тангенса, ЧХ будет сильнее
сжиматься по горизонтали и на частоте
Найквиста примет значение, которое ЧХ
аналогового фильтра имела бы на
бесконечной частоте. Выше сказанное
проиллюстрируем на рисунке ниже:
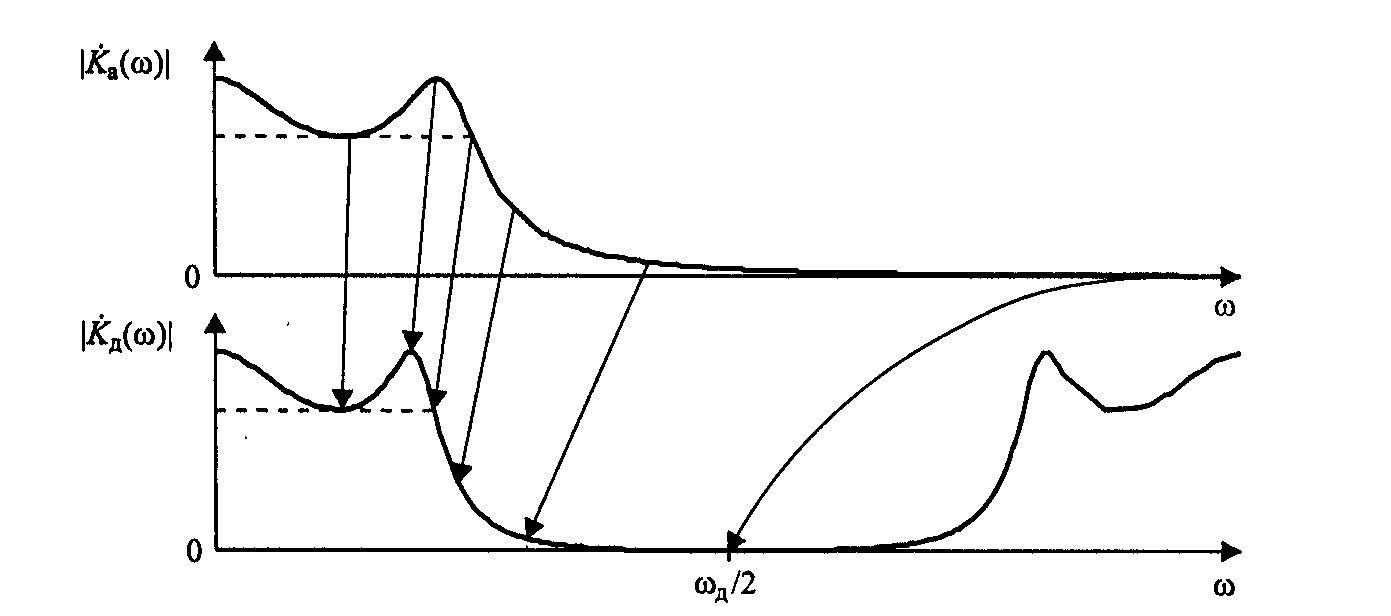
У какого фильтра нижних частот крутизна спада АЧХ больше — у аналогового прототипа или у дискретного фильтра, синтезированного по этому прототипу методом билинейного z-преобразования? Ответ обосновать.
Частотные характеристики аналогового KA(w) и дискретного KД(w) фильтров связаны друг с другом трансформацией частотной оси:
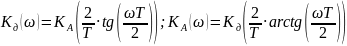
На низких частотах, когда wT<<1 тангенс примерно равен своему аргументу, поэтому в области НЧ АЧХ аналогового и дискретного фильтров почти совпадают. По мере роста ускорения функции тангенса, частотная характеристика дискретного фильтра все сильнее сжимается по горизонтали (по сравнению с прототипом). Т.е. АЧХ дискретного идет круче.
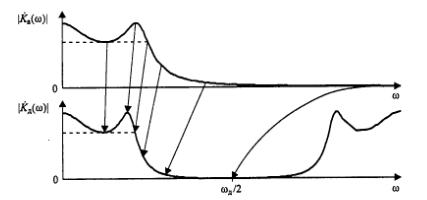
На каких частотах дискретный фильтр, синтезированный методом билинейного z‑преобразования, имеет такой же комплексный коэффициент передачи, как аналоговый прототип при частоте, стремящейся к бесконечности?
Частотные характеристики аналогового KA(ω) и дискретного KД(ω) фильтров связаны друг с другом трансформацией частотной оси:
На
частоте Найквиста, равной π/Т, ЧХ
дискретного фильтра достигает значения,
которое частотная характеристика
аналогового фильтра имела бы на
бесконечной частоте. И соответственно
такие же значения она будет иметь на
частотах: