3.7. Дифференциальные теоремы о среднем

Рассмотрим функцию , определенную на множестве . Точку называют внутренней точкой множества , если точка принадлежит множеству вместе с некоторой своей окрестностью.

Определение. Функция определена на множестве . Точка называется точкой локального минимума функции, если для всех точек из некоторой окрестности выполняется неравенство

.

Если выполняется строгое неравенство, т.е.

,

то точку называют точкой строгого локального минимума.

Соответственно, точка называется точкой локального максимума функции, если для всех точек из некоторой окрестности выполняется неравенство

.

Если выполняется строгое неравенство, т.е.

,

то точку называют точкой строгого локального максимума.

Точки локального максимума и локального минимума функции называют точками локального экстремума.

Теорема Ферма. Если функция имеет в точке локальный экстремум и дифференцируема в этой точке, то производная в точке равна нулю:

.

В теореме Ферма существенно, что точка, в которой достигается экстремальное значение, является внутренней точкой области определения функции.

Теорема Ролля. Если функция :

1. непрерывна на отрезке ,

2. дифференцируема в точках интервала ,

3. принимает на концах отрезка равные значения, т.е. ,

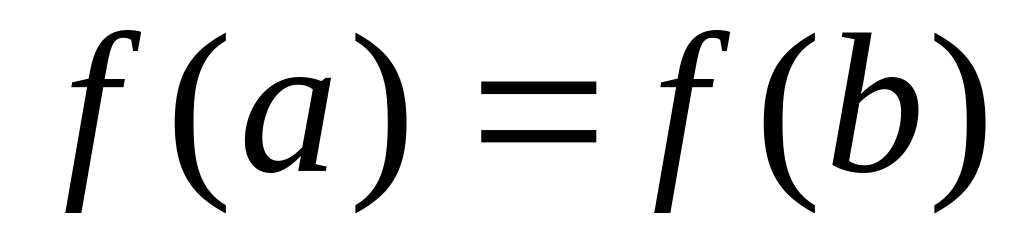то существует точка , в которой производная обращается в нуль

.

Теорему Ролля обобщает теорема Лагранжа.

Теорема Лагранжа. Если функция

1. непрерывна на отрезке ,

2. дифференцируема в точках интервала ,

то существует такая точка , что

.

Формула называется формулой конечных приращений Лагранжа.

Согласно этой теореме для дифференцируемой функции ее приращение в может быть вычислено через значение производной в некоторой средней точке. Геометрический смысл теоремы состоит в том, что отрезок, соединяющий концевые точки графика функции, параллелен касательной в некоторой средней точке графика.

И в заключение приведем результат, обобщающий сформулированные выше теоремы о среднем.

Теорема Коши. Если функции и

1. непрерывны на отрезке ,

2. дифференцируемы в точках интервала ,

3. производная во все точках , то существует точка , что

.

3.8. Раскрытие неопределенностей по правилу Лопиталя

Приведенная ниже теорема позволяет сравнительно просто вычислять пределы отношений бесконечно малых с помощью производных.

Теорема 1. Если для функций и выполняются условия:

1. функции дифференцируемы на интервале ,

2. производная во всех точках ,

3. ,

4. существует предел ,

то существует предел .

Теорема 2. Если для функций и выполняются условия:

1. функции дифференцируемы на интервале ,

2. производная во всех точках ,

3. ,

4. существует предел ,

то существует предел .

Теоремы 1 и 2 выражают суть правила Лопиталя, состоящую в том, что предел отношения бесконечно малых или бесконечно больших при соблюдении перечисленных выше условий может быть вычислен как предел отношения их производных.

Пример.

= = =

=