34.Нахождение фокусов, эксцентриситета, директрис гиперболы, если известно ее каноническое уравнение.

Эксцентриситет гиперболы

Определение. Отношение называется эксцентриситетом гиперболы, где с –

половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с2 – а2 = b2:

Если а = b, e = , то гипербола называется равнобочной (равносторонней).

Директрисы гиперболы

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .

Теорема. Если r – расстояние от произвольной точки М гиперболы до какого- либо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.

35.Определение параболы. Фокус и директриса параболы.

Парабола. Параболой называется геометрическое место точек, каждая из которых одинаково удалена от заданной фиксированной точки и от заданной фиксированной прямой. Точка, о которой идет речь в определении, называется фокусом параболы, а прямая - ее директрисой.

36.Каноническое уравнение параболы. Параметр параболы. Построение параболы.

Каноническое уравнение параболы в прямоугольной системе координат: (или , если поменять местами оси).

Построение параболы при заданной величине параметра p выполняется в следующей последовательности:

Проводят ось симметрии параболы и откладывают на ней отрезок KF=p;

Через точку K перпендикулярно оси симметрии проводят директрису DD1;

Отрезок KF делят пополам получают вершину 0 параболы;

От вершины отмеряют ряд произвольных точек 1, 2, 3, 5, 6 с постепенно увеличивающемся расстоянием между ними;

Через эти точки проводят вспомогательные прямые перпендикулярные оси параболы;

На вспомогательных прямых делают засечки радиусом равным расстоянию от прямой до директрисы;

Полученные точки соединяют плавной кривой.

37.Нахождение фокуса и директрисы параболы, если известно ее каноническое уравнение.

38.Общие характеристики эллипса, гиперболы, параболы. Геометрический смысл эксцентриситета.

Теорема. Сечение прямого кругового бесконечного в обе стороны конуса плоскостью, не проходящей через вершину, является или эллипсом, или гиперболой, или параболой. При этом, указанная плоскость может располагаться тремя способами:

1.пересекать одну половину конуса, в этом случае получается эллипс;

2.пересекать обе половины конуса, в этом случае получается гипербола;

3.быть параллельной образующей конуса, в этом случае получается парабола.

39.Приведение уравнения кривой второго порядка к каноническому виду методом выделения полных квадратов.

Пример. Привести уравнение кривой второго порядка к каноническому виду и построить кривую.

Решение.

Для приведения уравнения кривой второго порядка к каноническому виду применяют метод выделения полного квадрата.

Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при и вынесем за скобки:

Выделим полный квадрат: . Отсюда . Разделим обе части равенства на 25: . Запишем полученное уравнение в каноническом виде: .

Выполним параллельный перенос осей координат по формулам . При таком преобразовании начало координат переносится в точку , уравнение эллипса принимает канонический вид .

В нашем примере , , , .

Итак, рассматриваемое уравнение определяет эллипс с центром в точке и полуосями и 5.

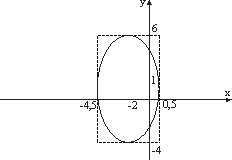
Рис. 13

Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования. Если ряд сходится, то предел общего члена равен 0 (необходимое условие сходимости ряда). Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом может расходиться. Необходимый признак в достаточной форме: если предел не равен 0, то ряд расходится.