25.Приведение квадратичной формы к диагональному виду методом элементарных преобразований.
26.Приведение квадратичной формы к диагональному виду методом Лагранжа.
27.Канонический вид квадратичной формы. Положительный и отрицательный индексы инерции квадратичной формы. Ранг квадратичной формы.
Квадратичная форма
называется канонической, если все
т. е.
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.
1. Ортогональное
преобразование пространства
:
где
- собственные значения матрицы A.
2. Метод Лагранжа -
последовательное выделение полных
квадратов. Например, если
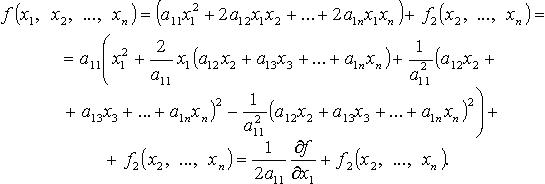
Затем подобную
процедуру проделывают с квадратичной
формой
и
т. д. Если в квадратичной форме все
но есть
то после предварительного преобразования
дело сводится к рассмотренной процедуре.
Так, если, например,
то полагаем
3. Метод Якоби (в случае,
когда все главные миноры
квадратичной формы отличны от нуля):
Пусть k(x) — квадратичная форма, заданная в пространстве арифметических векторов Rn.
В пространстве Rn существует канонический базис квадратичной формы, базис, в котором матрица квадратичной формы является диагональной.
В этом базисе квадратичная форма имеет канонический вид
k(x) = λ1x12 + λ2x22 + ... + λnxn2.
Числа λ1, λ2, ... , λn — канонические коэффициенты квадратичной формы.
Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэфициентов квадратичной формы не зависит от преобразования, с помощью которого квадатичная форма приводится к каноническому виду.
Число положительных канонических коэфициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэфициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность между положительным и отрицательным индексами квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.
28.Положительно определенные квадратичной формы. Критерий Сильвестра.
29.Определение эллипса. Фокусы эллипса.
Определение. Эллипс
- это геометрическая фигура, которая
ограничена кривой, заданной уравнением
.
Чертёж элипса
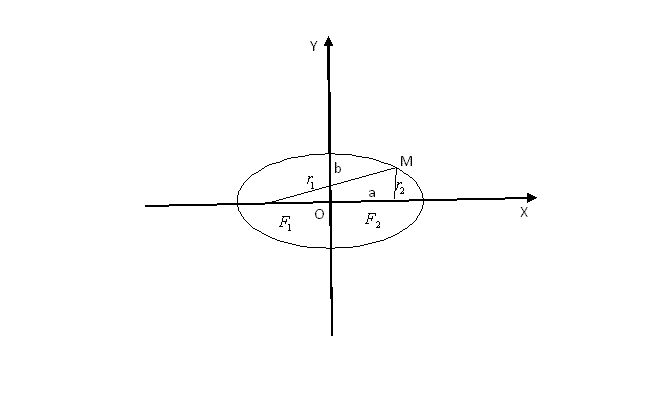
F1 , F2 – фокусы . F1 = ( c ; 0); F 2 (- c ; 0)
с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.
Теорема. Фокусное расстояние и полуоси связаны соотношением:
a2 = b 2 + c 2.
Доказательство: В
случае, если точка М находится на
пересечении эллипса с вертикальной
осью, r1 + r2 = 2*
(по теореме Пифагора). В случае, если
точка М находится на пересечении его с
горизонтальной осью, r1 + r 2 = a – c + a + c.
Т.к. по определению сумма r1 + r 2 – постоянная
величина, то , приравнивая, получаем:
a 2 = b 2 + c 2
r1 + r2 = 2 a .
30.Каноническое уравнение эллипса. Полуоси эллипса. Построение эллипса, если известно его каноническое уравнение.
Каноническое уравнение эллипса имеет вид
где a – большая полуось; b – малая полуось. Точки F1(c,0) и F2(-c,0) − c называются
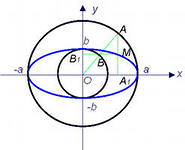
a, b - полуоси эллипса.
31.Нахождение фокусов, эксцентриситета, директрис эллипса, если известно его каноническое уравнение.
32.Определение гиперболы. Фокусы гиперболы.
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.
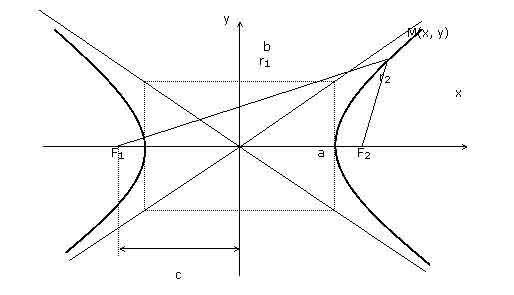
По определению |r1 – r2|= 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c.
33.Каноническое уравнение гиперболы. Полуоси гиперболы. Построение гиперболы, если известно ее каноническое уравнение.
Каноническое уравнение:
Большая полуось гиперболы составляет половину минимального расстояния между двумя ветвями гиперболы, на положительной и отрицательной сторонах оси (слева и справа относительно начала координат). Для ветви расположенной на положительной стороне, полуось будет равна:
Если выразить её через коническое сечение и эксцентриситет, тогда выражение примет вид:
Прямая, содержащая большую ось гиперболы, называется поперечной осью гиперболы.