42.Кривые заданные параметрически. Примеры. Построение параметрически заданной кривой.

При построении кривых, заданных параметрически:

x = x ( t ), y = y ( t ), можно придерживаться следующего плана.

Найти области определения D x ( t ) и D y ( t ) функций x ( t ) и y ( t ).

Найти область определения

функции, заданной параметрически.

Решив уравнения

x ( t ) = 0, y ( t ) = 0, найти точки пересечения с осями координат.

Вычислить производные и

Определить производную Найти критические точки.

На каждом из интервалов, границами которых служат критические точки, определить знак производной и промежутки возрастания и убывания функции y ( x ), заданной параметрически.

Определить экстремумы функции, а также точки, касательная к которым вертикальна (производная в этих точках обращается в бесконечность).

Определить особые точки графика, в которых и (или)

Найти пределы и в точках t 0, лежащих на границах области определения.

Если оба предела конечны, найти касательную к кривой в точке

Если один из пределов конечен, а второй бесконечен, то кривая имеет горизонтальную y = y 0 или вертикальную x = x 0 асимптоту.

Если оба предела бесконечны, то найти наклонную касательную, вычислив пределы Если один из этих пределов не существует, то асимптоты нет.

Вычислить производную и определить точки перегиба функции и направление выпуклости на каждом из интервалов, ограниченных точками перегиба или точками, в которых вторая производная не существует.

Выяснить, существуют ли точки самопересечения графика функции, решив систему

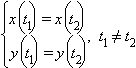
Проверить график функции на симметричность.

График функции симметричен относительно точки ( a ; b ), если при любом t можно найти такое t 1, что

График функции симметричен относительно прямой ax + by + c = 0, если при любом t можно найти такое t 1, что 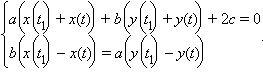В частности, график функции симметричен относительно прямой y = x , если при любых t имеет решение система

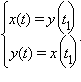
43.Эллипсоид. Однополостный и двуполостный гиперболоиды. Канонические уравнения. Вид поверхностей.

Эллипсо́ид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.

однополостный гиперболоид

где a и b — действительные полуоси, а c — мнимая полуось

двуполостный гиперболоид

где a и b — мнимые полуоси, а c — действительная полуось

44.Конус. Эллиптический и гиперболический параболоиды. Канонические уравнения. Вид поверхностей.

Ко́нус (от др.-греч. κώνος «шишка») — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Также можно сказать, что это тело, полученное при вращении прямоугольного треугольника вокруг одного из его катетов. Далее будет рассматриваться именно этот случай, если не оговорено обратное. Если основание конуса представляет собой многоугольник, такой конус является пирамидой.

Канонические уравнения

45.Эллиптический, параболический и гиперболический цилиндры. Канонические уравнения. Вид поверхностей.

46.Приведение уравнения поверхности второго порядка к каноническому виду методом выделения полных квадратов.

47.Построение поверхностей методом сечений.

48.Цилиндрическая и сферическая системы координат. Примеры поверхностей, заданных в цилиндрической и сферической системах координат.

Сферическими координатами называют систему координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат , где — расстояние до начала координат, а и — зенитный и азимутальный угол соответственно.

Понятия зенит и азимут широко используются в астрономии. Вообще зенит — это направление вертикального подъёма над произвольно выбранной точкой (точкой наблюдения), принадлежащей так называемой фундаментальной плоскости. В качестве фундаментальной плоскости в астрономии может быть выбрана плоскость, в которой лежит экватор, или плоскость, в которой лежит горизонт, или плоскость эклиптики и т. д., что порождает разные системы небесных координат. Азимут — угол между произвольно выбранным лучом фундаментальной плоскости с началом в точке наблюдения и другим лучом этой плоскости, имеющим общее начало с первым.

Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой ), которая задаёт высоту точки над плоскостью.