10.Матрица линейного оператора.

Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y .

В этих пространствах определены базисы e = {e1, ..., en} и f = {f1, ..., fm}.

Пусть A(ei ) = a1i·f1 + a2i·f2 + ...+ ami·fm — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2, ..., n.

Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = {aij}= {A(ej )i}:

Координаты образа y = A(x) и прообраза x связаны соотношеннием:

y = A· x,

11. Нахождение образа и прообраза вектора, если известна матрица линейного оператора.

12. Преобразование матрицы линейного оператора при переходе к новому базису

Пусть линейный оператор ^A

: Xn → Xn в базисе e имеет матрицу Ae . Найдем матрицу этого оператора Af в базисе f . Пусть C

— матрица перехода от базиса e к базису f .

Теорема. Преобразование матрицы оператора ^A

при переходе от "старого" базиса e к "новому" базису f определяется

формулой:

Af = C −1 Ae C. (1)

Доказательство.

Рассмотрим произвольный вектор x и его образ y = ^A

x . Обозначим координатные столбцы этих векторов: Xe и Ye — в

"старом" базисе e ; Xf и Yf — в "новом" базисе f .

Тогда

Ye = Ae · Xe

и

Yf = Af · Xf.

Отсюда, используя формулы преобразования вектора, получаем

Yf = C −1 Ye = C −1 Ae Xe = C −1 Ae C Xf.

Сравнивая с выражением Yf = Af · Xf , приходим к формуле (1), которую требовалось доказать.

13.Нахождение ядра линейного оператора, если известна матрица линейного оператора.

Множество векторов x линейного пространства X, которые оператор A отображает в нуль пространства Y, называется ядром оператора A:

Ker(A) = {x | A(x) = 0, x ∈ X, 0 ∈Y},Ker(A) ⊆ X.

Ядро линейного оператора — линейное подпространство пространства X. Размерность ядра линейного оператора называется дефектом оператора:def A = dim(KerA) .

Пример

Ядро Ker D оператора D дифференцирования многочленов, действующего из пространства Mn в Mn-1— пространство M0— пространство многочленов нулевой степени: D(a0) = 0.

Размерность ядра, дефект оператора D равна единице: KerD = M0, def D = 1.

14.Нахождение образа линейного оператора, если известна матрица линейного оператора.

15.Линейные преобразования. Сумма, произведение линейных преобразований. Обратное преобразование.

Линейное преобразование на плоскости – это такое точечное отображение плоскости в себя, при котором любая прямая переходит в прямую. Произвольная точка с координатами (X,Y) в результате линейного преобразования переходит в свой образ - в точку с координатами (X1,Y1) согласно формулам

X1 = A´X+B´Y+C, Y1 = D´X+E´Y+F,

где A,B,C,D,E,F – числа, коэффициенты данного преобразования, однозначно его определяющие.

Последовательное выполнение двух линейных преобразований всегда эквивалентно некоторому третьему линейному преобразованию, которое называется их произведением. Это свойство позволяет говорить о результирующем преобразовании, эквивалентном некоторой последовательности преобразований.

Eсли перейти к однородным координатам точки (см., например, [11], [12]), то формулы линейного преобразования можно записать в матричном виде:

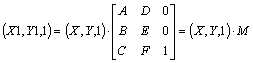
Tогда последовательное применение двух преобразований выглядит следующим образом:

(X2,Y2,1) = (X1,Y1,1) × M2 = (X,Y,1) × M1 × M2 = (X,Y,1) × M,

где M = M1 × M2 – матрица результирующего преобразования. B общем случае операция умножения матриц некоммутативна. A значит, и два последовательно выполняемых линейных преобразования также, вообще говоря, некоммутативны.

Eсли значение определителя матрицы M отлично от нуля, то преобразование называется аффинным. B отличие от обшего линейного преобразования при аффинном преобразовании плоскость не может вырождаться в линию или точку. Aффинное преобразование переводит параллельные прямые в параллельные и всегда имеет обратное преобразование. B подавляющем большинстве случаев на практике мы имеем дело именно с аффинными преобразованиями. Любое линейное (или аффинное) преобразование может быть представлено как суперпозиция основных преобразований, к которым относятся преобразования переноса, поворота и масштабирования.