4.Линейная зависимость и независимость элементов линейного пространства.
Линейная зависимость и независимость векторов. Базис.
Определение. Векторы
называются линейно зависимыми, если
существует такая линейная комбинация
,
при не равных нулю одновременно ai
, т.е.
.
Если же только при ai = 0 выполняется , то векторы называются линейно независимыми.
Свойство 1. Если среди
векторов
есть нулевой вектор, то эти векторы
линейно зависимы.
Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Свойство 6. Любые 4 вектора линейно зависимы.
Утверждение. Система векторов линейного пространства V является линейно зависимой тогда и только тогда, когда один из векторов является линейной комбинацией векторов этой системы.
Определение. Базисом линейного пространства V называется такая конечная упорядоченная линейно независимая система n векторов, что любой вектор пространства V является линейной комбинацией этих векторов (т.е. любая система из n+1 векторов является линейно зависимой).
5. Разложение вектора по базису.
Линейной комбинацией векторов a1, ..., an с коэффициентами x1, ..., xn называется вектор
x1a1 + ... + xnan.
Чтобы разложить, вектор b по базисным векторам a1, ..., an, необходимо найти коэффициенты x1, ..., xn, при которых линейная комбинация векторов a1, ..., an равна вектору b,
x1a1 + ... + xnan = b,
при этом коэффициенты x1, ..., xn, называются координатами вектора b в базисе a1, ..., an.
6.Замена базиса в линейном пространстве. Изменение координат вектора при замене базиса.
7.Линейные подпространства. Сумма и пересечение подпространств. Прямая сумма подпространств.
Подпространство
Алгебраическое
определение: Линейное подпространство
или векторное подпространство ― непустое
подмножество
линейного пространства
такое, что
само является линейным пространством
по отношению к определенным в
действиям сложения и умножения на
скаляр. Множество всех подпространств
обычно обозначают как
.
Чтобы подмножество было подпространством,
необходимо и достаточно, чтобы
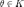;для всякого вектора
,
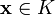вектор
также принадлежал
,
при любом
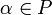;для всяких векторов
,
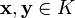вектор
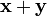также принадлежал
.
Последние два утверждения эквивалентны следующему:
для всяких векторов
,
вектор
также принадлежал
для любых
.
В частности, пространство,
состоящее из одного элемента
,
является подпространством любого
пространства; любое пространство
является само себе подпространством.
Подпространства, не совпадающие с этими
двумя, называют собственными или
нетривиальными.
Сумма и пересечение подпространств.
Пусть L1..Lk – линейные подпространства пространства V. Суммой подпространств L1..Lk называется множество всевозможных векторов x, представимых в виде x = x1 + … + xk, где xi из Li для любых i от 1 до k. Обозначается как L1 + L2 +.. + Lk
Представление вектора в виде такой суммы называется разложением вектора x по подпространствам L1.. Lk
Пересечением подпространств L1..Lk называется множество, в котором содержаться только те вектора, которые содержатся в каждом из подпространств L1..Lk
Пересечение пустым не бывает, как минимум это нулевой вектор.
Теорема. Сумма и пересечение подпространств линейного пространства V также является подпространством V.
Доказательство следует из определения подпространства.
Теорема. Сумма линейных подпространств есть линейная оболочка совокупности базисов слагаемых подпространств.
Доказательство – просто проверяем двустороннее вложение.
Следствие. Размерность суммы подпространств равна рангу мовокупности базисов слагаемых подпространств.
Теорема. Для любых двух подпространств выполняется равенство dim(L1+L2) = dimL1 + dim L2 – dim(L1^L2)
Доказательство.
Если пересечение ненулевое, то смотрим его базис – f1..fn – так как пересечение является подпространством каждого из исходных подпространств, этот базис можно дополнить до базиса каждого из подпространств. Дополним, получим два базиса. В каждом из них будет n векторов из базиса пересечения. А если дополнить до базиса совокупности сразу, получим n векторов из базиса пересечения и еще m и s дополняющих векторов до базиса первого и второго подпространства. То есть, m+s+n = m+n + s +n – s – верно, доказано.
Прямая сумма пространств
Пусть L -лин пространство и в нем есть 2 подпространства M и N
L есть прямая сумма M и N, если выполняются 2 условия
1)М пересек N ={0}
2)для всех x прин L сущ x1 прин M и сущ x2 прин N:x=x1+x2
Теорема: Пусть L=прямое пересечение M и N, тогда
1)x=x1+x2 x1 и x2 определяются единственным образом
2)Если e1,...,ek базис в M, а f1,...,fr базис в N, то e1,...,ek,f1,...,fr базис в L
Не всегда
3)dim L=dimM+dimN (следствие 2)
1)х=x1+x2=x1'+x2'
x1,x1' прин M
x2,x2' прин N
x1-x1'=x2'-x2 Так как между ними рав-во, то они принадлежат обоим множествам => x1=x1' x2=x2'
2)e1,...,ek базис в M, а f1,...,fr базис в N
1 свойство - лин нез
2 свойсвто - можно разложить по базису
2-ое
x=x1+x2=альфа1e1+...+альфаkek+бета1f1+...+бетаrfr
люб вектор можно разложить по базису
1-ое
Пусть альфа1e1+...+альфаkek+мю1f1+...+мюrfr=0, докажем что все коэфф=0
альфа1e1+...+альфаkek=-мю1f1-...-мюrfr
прин M прин N
обе суммы равны 0, но т.к. это базис они лин незав=> все коэфф=0