Тема 9. Моделирование процесса фотолитографии.

Основные этапы численного моделирования фотолитографии. Оптическая литография – стандартный технологический процесс формирования топологических рисунков при создании интегральных схем. Оптическая проекционная литография, в которой изображение объекта (маски) проецируется на подложку через сложную, имеющую дифракционные ограничения оптическую систему, все еще остается доминирующей технологией создания топологического рисунка в микроэлектронике.

Целью моделирования фотолитографии является получение расчетного профиля резистивной пленки по краю прорисовки как результата экспонирования и проявления резистивного слоя в ходе соответствующих технологических процессов. Такой профиль позволяет определять критические размеры элементов, формируемых в резистивной пленке, т.е. ширину линий и зазор, максимальную толщину резистивной пленки, наклон ее края и влияние эффектов стоячих волн на профиль пленки по краю прорисовки.

Для получения профиля резистивной пленки необходимо промоделировать ряд физических и физико-химических процессов, используемых в ходе выполнения литографической обработки:

1. Необходимо рассчитать распределение интенсивности света, падающего на поверхность резистивной пленки. Это распределение интенсивности, называемое также фронтальным изображением, зависит от оптической системы, используемой для проецирования изображения на поверхность. Для таких элементов топологии, как ширина линии в данном слое или зазор между линиями, необходим одномерный профиль распределения интенсивности на краю прорисовки. Для двумерных топологических объектов, например, контактных окон, требуется двумерное фронтальное изображение. Оно чаще всего прорисовывается в виде контуров равной интенсивности. Интенсивность I₀ в каждой точке фронтального изображения считается постоянной в течение всего времени экспонирования резистивного слоя. Таким образом, распределение интенсивности света I₀ зависит только от координат на поверхности резистивного слоя: I₀ = I₀(x, y).

2. Необходимо рассчитать интенсивность света в пленке как функцию глубины. Полная интенсивность I₀ уменьшается с глубиной в результате поглощения света резистивным материалом. Далее, отражение света от подложки вызывает наложение стоячих волн в пленке на распределение интенсивности по глубине. Наконец, материал резистивного слоя претерпевает химические изменения в процесс экспонирования, поэтому распределение интенсивности по глубине также меняется во времени и должно рассчитываться в каждый момент времени отдельно по каждой из имеющихся длин волн. Таким образом, распределение интенсивности света с длиной волны λ в пленке есть функция уже не только трех координат, но и времени: I_λ = I_λ(x, y, z, t).

3. На следующем шаге требуется рассчитать нормализованную концентрацию светочувствительного компонента (М) в позитивном резисте как функцию координат и времени. Окончательное значение М в каждой точке после завершения экспонирования есть один из параметров, определяющих скорость проявления резиста. При расчете концентрации светочувствительного компонента используются эмпирические соотношения, описывающие процесс отбеливания с коэффициентами, задаваемыми пользователем.

4. Определяется скорость проявления R(x,y,z) в каждой точке резистивной пленки. Скорость проявления зависит от таких параметров как локальная концентрация светочувствительного компонента, характеристики процесса задубливания, тип проявителя и температура, внутренние свойства материала резистивного слоя. В некоторых резистивных материалах имеет место эффект замедления скорости проявления на поверхности пленки, в этом случае данный эффект необходимо учесть при моделировании.

5. Собственно процесс проявления рассчитывается с использованием алгоритма продвижения струны. Структура резиста после завершения процесса проявления представляется в виде профиля края прорисовки.

Расчет изображения на поверхности фоторезиста. В литографическом процессе первой основной задачей является перенос изображения маски на поверхность фоторезиста. В идеальном случае интенсивность света должна быть нулевой внутри темных полей или линий и высокой в области зазоров между фигурами. Однако в реальности край изображения никогда не получается идеально резким.

Распределение интенсивности света на краю изображения определяется свойствами источника света и свойствами оптической системы. Если размеры источника света очень малы, и источник можно считать точечным, то при прохождении через линзу, в фокусе которой расположен источник, освещение становится практически когерентным. При когерентном освещении маски в распределении освещенности на поверхности пластины появляются дифракционные максимумы, как показано на рисунке 9.1,а.

а	б

Рисунок 9.1 Распределение освещенности в плоскости фоторезиста а) при когерентном освещении маски; б) при частично когерентном освещении.

Если источник света из-за конечности его линейных размеров нельзя считать точечным, то степень когерентности света, попадающего на маску, частично уменьшается. При уменьшении когерентности освещения дифракционные максимумы сглаживаются, т.к. происходит суммирование интенсивностей освещения, создаваемых различными угловыми компонентами светового поля и имеющих, следовательно, дифракционные максимумы в различных точках. С другой стороны, уменьшение когерентности излучения, эквивалентное расширению углового спектра, приводит к образованию полутени, как показано на рисунке 9.1, б, где Δх – ширина области полутени.

Итак, существуют два фактора, приводящих к деградации изображения края маски, но зависящих от размера источника света противоположным образом:

- дифракционные максимумы, которые уменьшаются при увеличении размера источника света;

- область полутени, которая увеличивается при увеличении размера источника.

Оптимальное значение размера источника света или оптимальная ширина его углового спектра зависит от типа проекционной системы. На рисунке 9.2 показаны два варианта проекционных систем.

Маска Маска	Источник Маска
а	б

Рисунок 9.2 Формирование изображения на поверхности фоторезиста а) методом проекционной печати; б) методом контактной с зазором печати.

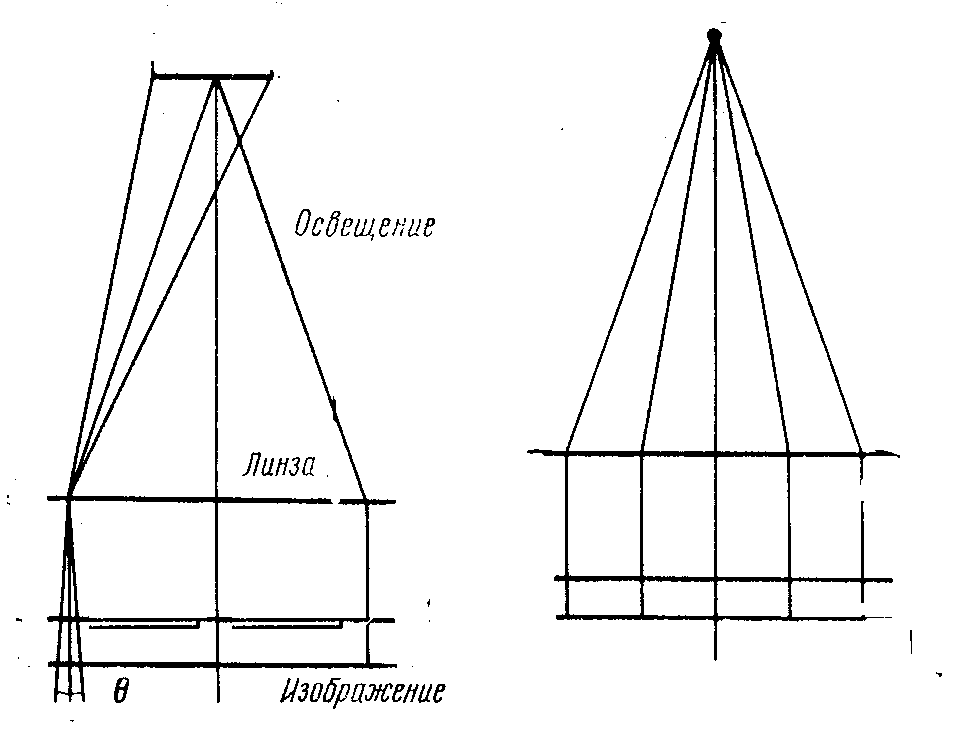
В проекционной литографии схема оптической системы (рисунок 9.2,а) включает две линзы: конденсорную и проекционную. Свет от источника проектируется конденсорной линзой в центр объективной линзы. Маска расположена вблизи конденсорной линзы, так что на нее падают плоские волны, и все элементы матрицы освещаются когерентно. Волны, которые, проходя через маску, рассеиваются внутри конуса с углом раствора θ₀, принимаются проекционной линзой и снова фокусируются на пластине, формируя изображение. Численные апертуры, равные синусам угла раствора, для конденсорной линзы NA_C = sin θ_C, и входа проекционной линзы NA₀ = sin θ₀, определяют степень когерентности σ = NA_C/ NA₀. Качество изображения в такой системе в основном определяется дифракцией. Максимальная разрешающая способность может быть оценена как 0.8λ/NA, где λ – длина волны излучения, NA – численная апертура выхода проекционной линзы NA = sin θ.

В схеме оптической системы, формирующей изображение по методу контактной печати с зазором, показанной на рисунке 6.2, б, используется только конденсорная линза. Оптимальное значение углового спектра, учитывающее и дифракцию, и образование полутени на краях изображения, может быть оценено с помощью эмпирической зависимости:

θ_ОРТ = 0.2 ∙ (1 + 2h λ/а ),

где а - ширина минимального элемента в рисунке маски.

Важной частью модели для расчета изображения на поверхности резистивной пленки являются параметры, характеризующие маску. Маски амплитудного типа характеризуются функцией пропускания интенсивности T(x, y), такой, что интенсивность освещения, прошедшего через маску, равна

I(x, y) = I₀∙ T(x, y),

где I₀- интенсивность освещения маски, считающаяся однородной по всей поверхности маски.

В результате рассеяния на маске каждой из падающих плоских волн образуется спектр когерентных дифрагированных плоских волн. Элементами конфигурации маски являются края и углы прямоугольных прозрачных окон, расположенных на непрозрачном фоне. Предполагая, что стороны прямоугольных окон параллельны осям X и Y системы координат, функцию I(x, y) можно представить в виде разложения в двумерный спектр Фурье:

I(x, y) = ∫∫ J (f_X,f_Y) exp[-2πi (f_X∙x + f_Y∙y)]df_X df_Y;

J (f_X,f_Y) = (2π)^-2 ∫∫ I(x, y) exp[2πi (f_X∙x + f_Y∙y)]dx dy,

где J (f_X,f_Y) – коэффициенты разложения Фурье для интенсивности освещения, прошедшего через маску, f_X, f_Y – пространственные частоты. Если границы между прозрачными и непрозрачными участками маски считать резкими и задавать их математически ступенчатой функцией, то в спектре разложения будут присутствовать компоненты J (f_X,f_Y) со сколь угодно большими пространственными частотами.

Расчет интенсивности освещения в пленке фоторезиста. При расчете интенсивности освещения в пленке в процессе экспонирования фоторезиста необходимо учитывать следующие физические и химические факторы:

- интенсивность освещения на поверхности резистивной пленки;

- уменьшение интенсивности с глубиной, связанное с поглощением света материалом пленки;

- отражение света от подложки и возникновение вертикальных стоячих волн;

- распад светочувствительного компонента в процессе экспонирования (отбеливание фоторезиста) в результате химических реакций и, как следствие, зависимость свойств материала пленки от времени.

Таким образом, при расчете данного процесса требуется моделирование нестационарного процесса отбеливания материала резиста и его влияния на распределение интенсивности изображения. Интенсивность света в пленке рассчитывается как функция координат на каждом дискретном интервале времени Δt и для каждой длины волны.

При моделировании процесса отбеливания позитивного фоторезиста считается, что он имеет комплексный коэффициент преломления, зависящий от нормированной концентрации светочувствительного компонента М и, следовательно, изменяющийся в процессе экспонирования:

n = n_r – iλ(A∙M + B)/(4π),

где n_r – реальная часть коэффициента преломления, A + B – коэффициент поглощения неотбеленного резиста, B – коэффициент поглощения полностью отбеленного резиста, M изменяется от 1 до 0 в ходе экспонирования. Непосредственно коэффициент поглощения может быть рассчитан как α = A∙M(x, y, z, t) + B.

Значение М соответствует доли светочувствительного вещества, оставшегося в фоторезисте и его изменение описывается дифференциальным уравнением

dM/dt = - I(x, y, z, t) ∙ M(x, y, z, t) ∙ C,

где I(x, y, z, t) – локальная интенсивность света, C – чувствительность фоторезиста к отбеливанию.

Расчет распределения интенсивности по толщине пленки на каждом временном интервале рассчитывается с помощью алгоритма, представленного на рисунке 9.3. Схема расчета позволяет учесть наличие кроме фоторезиста тонких диэлектрических слоев на поверхности непрозрачной подложки. Вся структура разбивается на тонкие слои, малая толщина которых позволяет рассматривать их как слои с изотропными свойствами. Для этого толщина каждого подслоя не должна превышать 0.03λ.

Рисунок 9.3 Схема алгоритма анализа прохождения света в тонких пленках.

Расчет пропускания и отражения проводится на каждой границе раздела, начиная от поверхности. Определяются комплексные коэффициенты отражения r_j и пропускания t_j, затем рассчитывается поглощение в каждом тонком слое. Рассчитывается также амплитуда стоячей волны, которая зависит от толщины пленки и оптических коэффициентов. Резист отбеливается (доля светочувствительного вещества М уменьшается) в каждом подслое согласно взвешенной интенсивности и чувствительности С для каждой длины волны, и результаты суммируются по всему спектру длин волн. На следующем временном шаге t + Δt расчеты повторяются с использованием уже полученных результатов в качестве начальных условий. На рисунке 9.4 приведен пример расчетных кривых для распределения интенсивности света в пленке фоторезиста и соответствующему данной интенсивности распределению нормированной концентрации светочувствительного компонента.

I

М

D,

мкм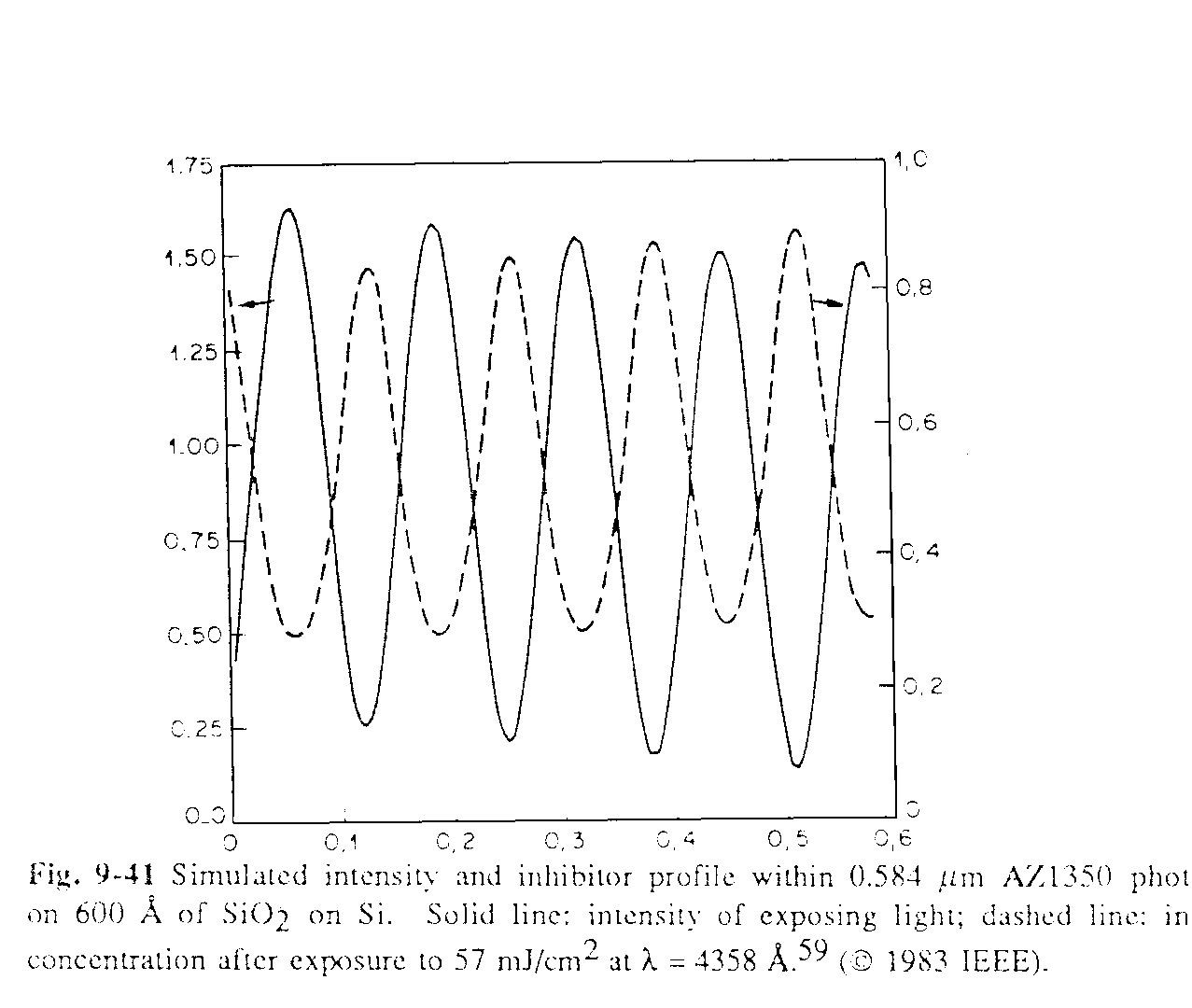

Рис. 9.4 Расчетные распределения интенсивности света (сплошная линия) и концентрации светочувствительного компонента (пунктир) в пленке фоторезиста толщиной 0.584 мкм.

Выходной информацией при расчете на данном этапе является распределение нормализованной концентрации светочувствительного компонента (ингибитора) по глубине для произвольной точки изображения маски. После окончания экспонирования результаты представляют собой матрицу значений M(x, y, z). Термообработка, проводимая непосредственно после экспонирования до начала процесса проявления (прокаливание), призвана сгладить волнистость профиля распределения M(x, y, z, t) на краях элементов изображения, вызванную модуляцией интенсивности освещения за счет стоячих волн. Новое распределение в этом случае может быть получено путем моделирования процесса диффузии ингибитора в пленке еще не проявленного резиста с использованием обычных моделей для расчета диффузии примеси.

Моделирование процесса проявления. Процесс проявления экспонированного фоторезиста с точки зрения моделирования представляет собой процесс поверхностного травления, для которого в полной мере можно использовать обычные модели травления (См. раздел «Моделирование травления и осаждения слоев»), в частности алгоритм струны и его модификации. Для выполнения расчета профиля резистивной пленки после проявления необходимо задать распределение локальной скорости травления от координат R = R(x, y, z).

Скорость локального травления зависит от концентрации светочувствительной компоненты М, которая одновременно является замедлителем (ингибитором) для реакции растворения пленки. При отбеливании резиста светочувствительная компонента разрушается с выделением органической кислоты, которая является ускорителем в процессе проявления. Можно считать, что доля органической кислоты (ускорителя) пропорциональна (1-М). Если учесть эффекты ускорения, пропорционального (1-М), и замедления, пропорционального М, результирующее выражение для скорости травления химически однородных резистов будет иметь вид:

1/R(M) = (1-M∙P)/R₁ + M∙P/R₂ ,

или более подробно:

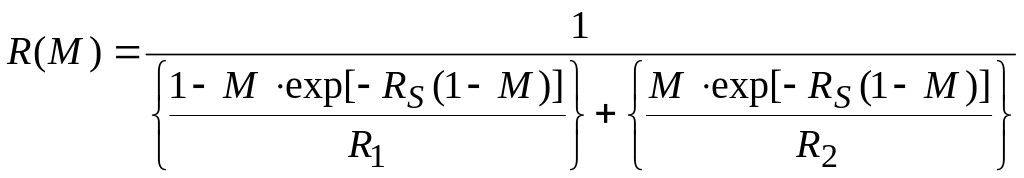
где R₁ и R₂ – скорости травления соответственно полностью отбеленного и неотбеленного материалов, P = exp[-R_S∙(1-M)], R_S – безразмерный параметр, характеризующий чувствительность скорости травления к изменению концентрации ингибитора.

Для расчета локальной скорости травления можно использовать также более простое выражение, основанное на полиномиальной аппроксимации экспериментальных зависимостей:

R(M) = exp(E₁ + E₂∙M + E₃∙M²).

При использовании таких эмпирических выражений приходится учитывать зависимость значений коэффициентов E₁, E₂, E₃ не только от типа материала резиста, но и от температуры термообработки перед проявлением. Например, для резиста AZ1350J E₁=5.63, E₂=7.43, E₃= -12.6, если температура термообработки 70°С, и E₁=4.39, E₂=5.69, E₃= -9.0, если температура термообработки 100°С.

Расчет процесса проявления методом продвижения струны начинается с поверхности резиста. На первом шаге точки закрепления струны параллельны поверхности резистивной пленки. Затем они начинают продвижение согласно локальной скорости R[M(x, y, z)]. Узлы, находящиеся в сильно засвеченной зоне, быстро продвигаются вниз, освобождая центр экспонированного участка, и затем смещаются в стороны к не проявленным зонам, формируя краевой профиль. Типичный профиль края линии в фоторезисте, полученный в результате моделирования в программе SAMPLE, показан на рисунке 9.5.

Рисунок 9.5. Типичный профиль края линии в фоторезисте AZ1350J, рассчитанный в программе SAMPLE; время проявления 85 с.

Ширина линии особенно существенно изменяется вблизи ступенек на подложке, где меняется толщина пленки и есть дополнительные факторы, воздействующие на профиль резиста. Анализ таких эффектов требует расчета двух- и трехмерных распределений освещенности и светочувствительного компонента при моделировании литографического процесса.

H

w₂

w₁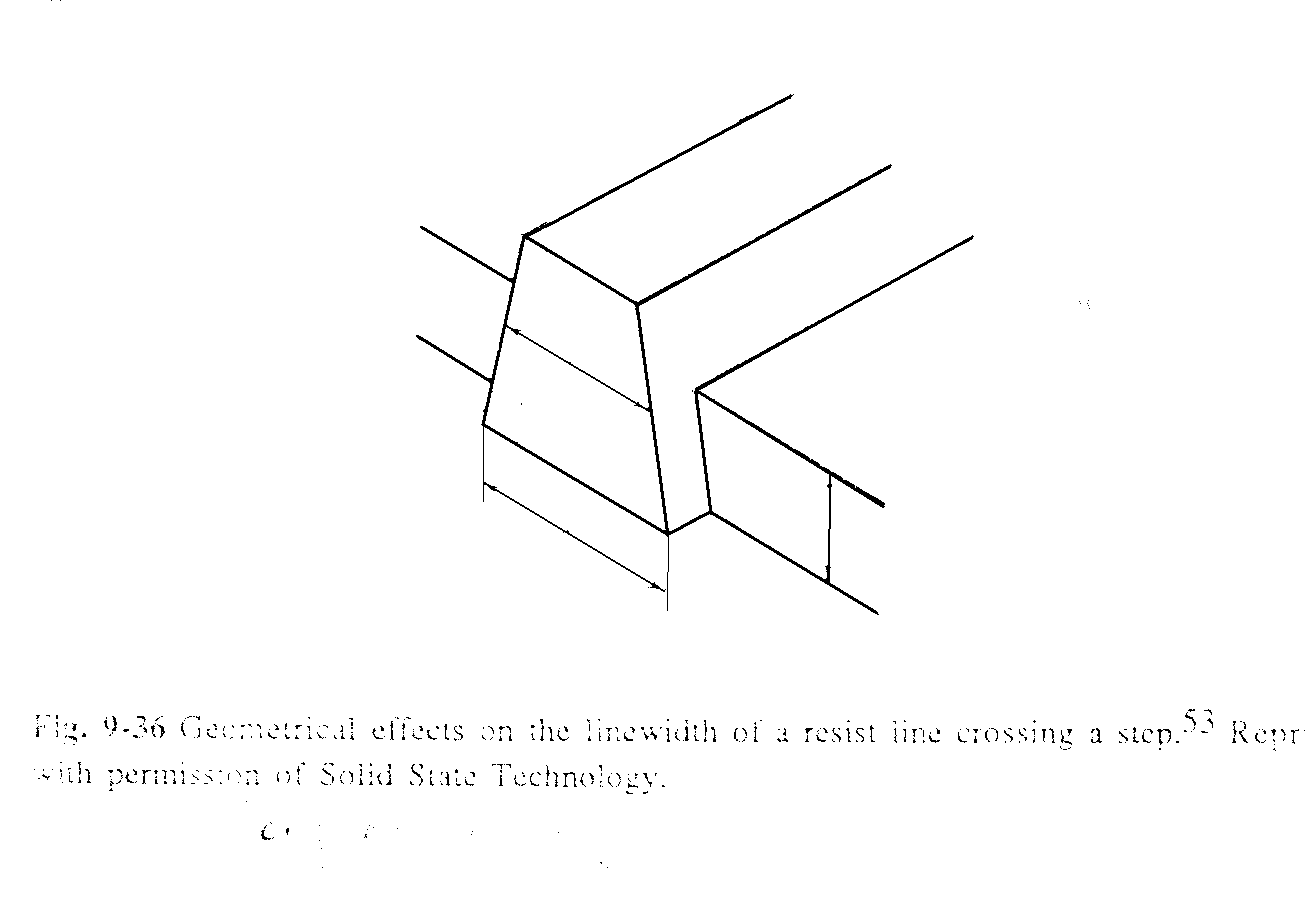

Рисунок 9.6 Изменение толщины линии при переходе через ступенчатый рельеф подложки.

На рисунке 9.6 показано изменение ширины резистивной полоски при пересечении ступеньки высотой H. Простая оценка вариации ширины может быть легко сделана, если известен средний угол отклонения боковых стенок резистивного слоя от вертикального направления α_Р:

Δw = w₂ – w₁ = H∙ tg α_Р

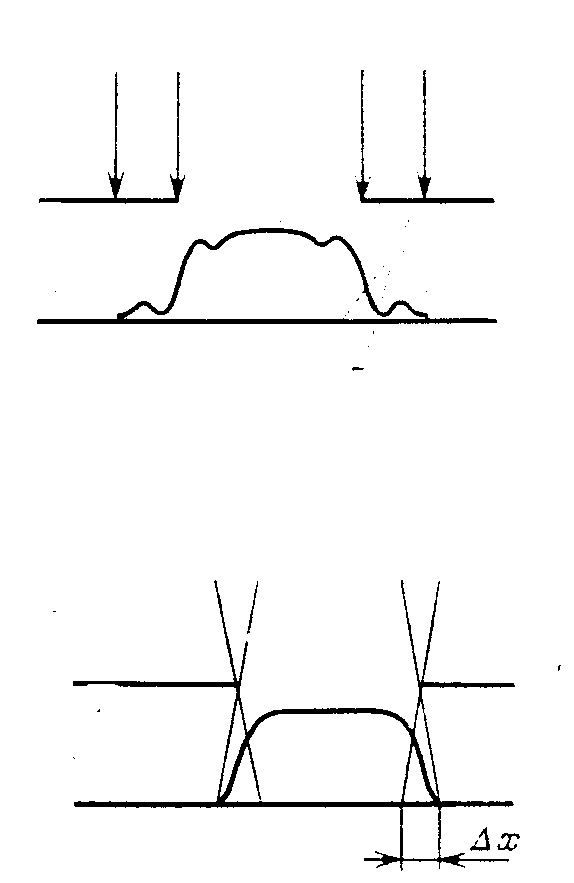
Кроме основного скачка на ступеньке ширина линии периодически модулируется по обе стороны ступеньки, что связано с наличием максимумов и минимумов коэффициента отражения. Другим примером влияния рельефа поверхности подложки на ширину резистивного слоя является эффект возникновения выемки, показанный на рисунке 9.7. Как видно из рисунка, сужение или выемка на резистивном слое связана с наличием узкой ступеньки или ее края. В этом случае отражение света от боковой поверхности ступеньки при экспонировании приводит к дополнительному засвечиванию резиста и повышению скорости проявления резиста в данной области.

Резист

Отражающий слой

Падающий свет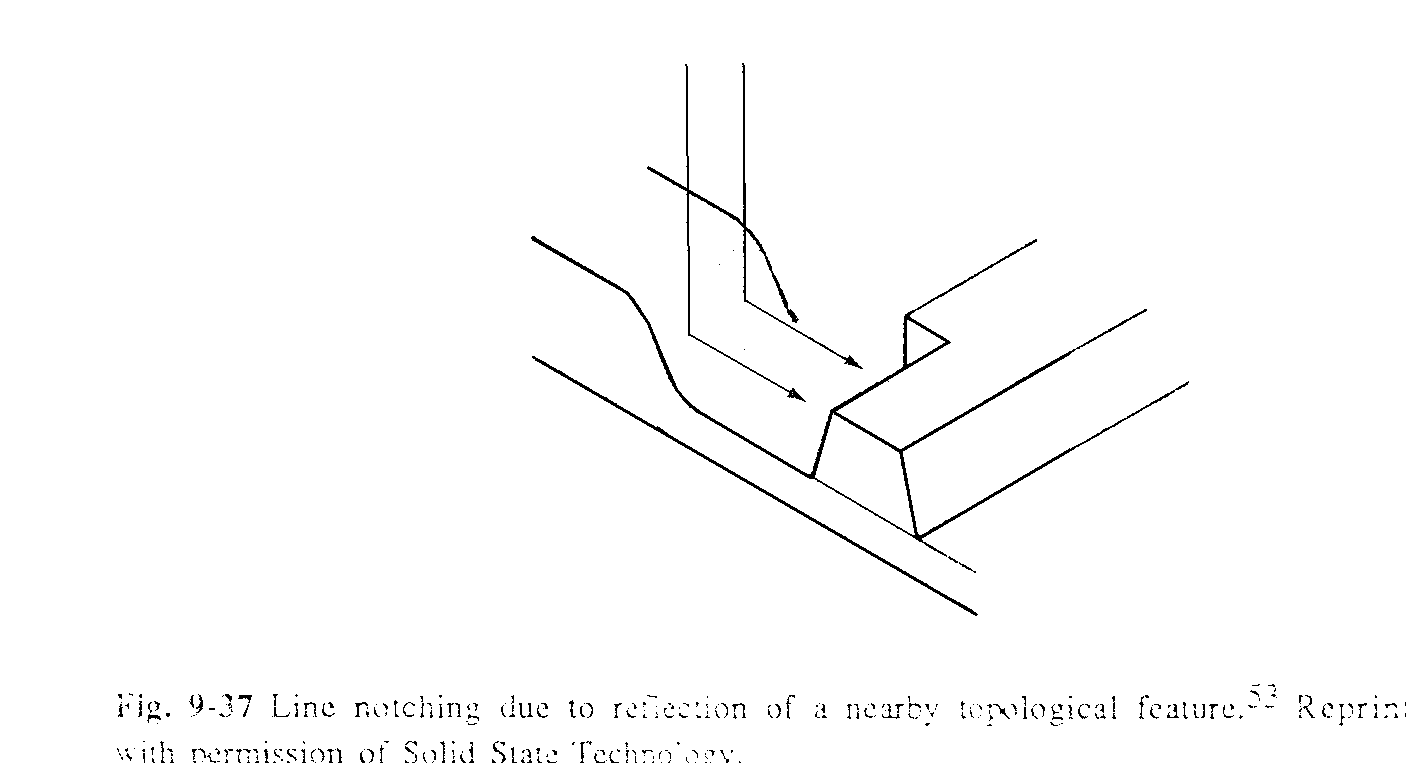

Рисунок 9.7 Возникновение выемок на линии позитивного резиста из-за дополнительного отражения от рельефа подложки.

Вопросы по теме 9:

1. Что является целью при моделировании процесса фотолитографии?

2. Перечислите основные этапы при моделировании процесса фотолитографии.

3. Проиллюстрируйте распределение освещенности в плоскости фоторезиста при когерентном и частично когерентном освещении маски.

4. Какие факторы приводят к деградации изображения края маски, и как они зависят от размера источника света?

5. Какие процессы необходимо учитывать при расчете интенсивности освещения в пленке в процессе экспонирования фоторезиста?

6. Запишите уравнение, характеризующее изменение доли светочувствительного компонента, оставшегося в фоторезисте.

7. От чего зависит скорость травления химически однородных резистов. Приведите формулу зависимости.

8. Нарисуйте типичный профиль края линии в фоторезисте.

9. Как влияет рельеф на ширину воспроизводимых линий?

10. С чем связано возникновение выемок на линии позитивного резиста?