Тема 10. Методы численного моделирования полупроводниковых приборов.

В основе численного моделирования полупроводниковых приборов лежит решение системы уравнений в частных производных, описывающей статическое и динамическое поведение носителей в полупроводнике под влиянием внешних полей. Часть уравнений, входящих в эту базовую систему, могут быть получены из уравнений Максвелла, а уравнения переноса – путем последовательного вычисления моментов классического кинетического уравнения Больцмана. Решение интегродифференциального уравнения Больцмана представляет сложную проблему, особенно в случае пространственно неоднородных явлений. Обычно используется квазистатическое приближение, которое справедливо, если произведение максимальных скоростей носителей и времен релаксации пренебрежимо мало по сравнению с активными размерами прибора. Используя вычисление двух моментов кинетического уравнения Больцмана, получаем хорошо известную диффузионно-дрейфовую модель. В результате вычисления третьего момента получается уравнение баланса энергии, с учетом которого строится гидродинамическая модель. В этом случае в уравнения непрерывности необходимо ввести температурную зависимость коэффициентов.

Таким образом, из уравнений Максвелла получаем уравнение Пуассона и уравнения непрерывности:

div (εּgradψ) = -ρ;

= div Jn + (G – R);

= div Jр + (G – R);

из уравнения Больцмана либо диффузионно-дрейфовую модель:

Jn = - qμ nּgrad φ ;

Jp = - qμ pּgrad φ ;

либо гидродинамическую модель:

Jn = μ (nּgrad Ec + k T grad n);

Jp = μ (pּgrad Ev + k T grad p);

+ div Sn = Jnּgrad Ec + ;

+ div Sp = Jpּgrad Ev + ;

+ div S = ;

где ε – диэлектрическая проницаемость; ψ – электростатический потенциал; ρ – плотность объемного заряда; ρ = -qּ(n – p + N); n, p – концентрация электронов и дырок, соответственно; N – алгебраически суммарная концентрация электрически активной примеси; Jn, Jp – плотность электронного и дырочного тока, соответственно; (G – R) – суммарный вклад процессов генерации – рекомбинации носителей; μ , μ - подвижности электронов и дырок, соответственно; φ , φ - квазиуровни Ферми для электронов и дырок; Ec, Ev – энергии зоны проводимости и валентной зоны, соответственно; k - константа Больцмана; T , T , Т - эффективная температура электронов, дырок и решетки, соответственно; Wn, Wp, W и Sn, Sp, S - энергия и энергетический поток электронов, дырок и решетки, соответственно.

Базовые уравнения численного моделирования полупроводниковых приборов в дрейфово-диффузионном приближении:

Уравнение Пуассона div (εּgradψ) = -ρ;

Уравнения непрерывности: = div Jn + (G – R);

= div Jр + (G – R);

Уравнения переноса Jn = - qμ nּgrad φ ;

Jp = - qμ pּgrad φ ;

где ε – диэлектрическая проницаемость; ψ – электростатический потенциал; ρ – плотность объемного заряда; ρ = -qּ(n – p + N); n, p – концентрация электронов и дырок; N – алгебраически суммарная концентрация электрически активной примеси; Jn, Jp – плотность электронного и дырочного тока; (G – R) – суммарный вклад процессов генерации – рекомбинации носителей; μ , μ -подвижности электронов и дырок; φ , φ - квазиуровни Ферми для электронов и дырок.

Базовые уравнения численного моделирования полупроводниковых приборов для термодинамической модели.

В термодинамическом приближении учитываются термоэлектрические эффекты, связанные с неоднородным распределением температуры.

Уравнение Пуассона div (εּgradψ) = -ρ;

Уравнения непрерывности: = div Jn + (G – R);

= div Jр + (G – R);

Уравнения переноса Jn = - qμ n (grad φ + grad T)

Jp = - qμ p (grad φ + grad T)

где ε – диэлектрическая проницаемость; ψ – электростатический потенциал; ρ – плотность объемного заряда; ρ = -qּ(n – p + N); n, p – концентрация электронов и дырок; N – алгебраически суммарная концентрация электрически активной примеси; Jn, Jp – плотность электронного и дырочного тока; (G – R) – суммарный вклад процессов генерации – рекомбинации носителей; μ , μ - подвижности электронов и дырок; φ , φ - квазиуровни Ферми для электронов и дырок, P_n, P_p – величины термоэдс для электронов и дырок, Т – температура (Т_n=T_p=T_L)

Системы дифференциальных уравнений в частных производных, описывающих процессы перераспределения примесей, роста слоев и структуру полупроводниковых приборов, в общем случае не имеют аналитического решения. Решение таких систем уравнений может быть найдено только численными методами. При этом приходится последовательно рассматривать три задачи:

• Вся геометрическая область, представляющая исследуемую структуру, должна быть разделена на конечное число подобластей, решение в которых может быть наиболее легко получено с требуемой точностью.

• В каждой из подобластей дифференциальные уравнения должны быть аппроксимированы алгебраическими уравнениями, которые включают только дискретные значения непрерывных переменных, входящих в систему дифференциальных уравнений.

• Должна быть решена, как правило, очень большая система нелинейных алгебраических уравнений, в которых неизвестные величины представляют собой аппроксимации непрерывных переменных в дискретных точках структуры.

Таким образом, нельзя получить точное решение задачи в целом, но можно получить в лучшем случае точное решение системы нелинейных алгебраических уравнений, отражающих дискретизованную постановку задачи. Такое решение представляет собой аппроксимацию, зависящую от дробности разбиения и аппроксимирующих функций, используемых для расчета значений переменных внутри элементов сетки.

Основные алгоритмы, используемые для дискретизации базовых уравнений при численном моделировании полупроводниковых приборов.

- метод конечных разностей (МКР);

- метод конечных элементов (МКЭ).

В методе конечных разностей сетка состоит из линий, параллельных осям координат. Шаг сетки может меняться.

а)

б)

Рисунок 10.1 – Метод конечных разностей: а – вид сетки; б – схема дискретизации.

+ …

В методе конечных элементов сетка треугольная или комбинированная прямоугольно-треугольная.

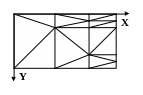
Рисунок 10.2 Вид сетки при использовании метода конечных элементов.

Значение функции внутри элемента:

Для треугольника u^a(x,y) = a₀ + a₁x + a₂y;

для прямоугольника u^a(x,y) = a₀ + a₁x + a₂y + a₃xy;

значения коэффициентов определяются по значениям функции в узлах сетки.

Существует ряд факторов, определяющих сходимость численного решения:

Базовые дифференциальные уравнения для моделирования полупроводниковых приборов после дискретизации могут быть представлены как система большого числа нелинейных алгебраических уравнений F(x)=0.

Система может быть решена итеративно методом Ньютона

.

Точность вычислений может быть потеряна при расчете правой части и при расчете Якобиана. Количественно распространение ошибки вычислений задается коэффициентом усиления ошибки, который определяется для функции y(x) следующим образом:

Сходимость зависит от:

• разрядности вычислительной системы (машинная точность);

• коэффициента усиления ошибки при расчете правой части;

• коэффициента усиления ошибки при расчете Якобиана;

• особенностей решаемой физической проблемы

Аппаратная точность определяется разрядностью используемой вычислительной системы и считается известной заранее. Степень нарастания ошибки при расчете правой части зависит, в основном, от параметров сетки, а для Якобиана – еще и от особенностей характеристик в рабочей точке (например, при расчете пробойных явлений).

Вопросы по теме 10:

1. Запишите базовые уравнения численного моделирования полупроводниковых приборов в дрейфово-диффузионном приближении.

2. Запишите базовые уравнения численного моделирования полупроводниковых приборов для термодинамической модели.

3. Какие последовательные этапы включает задача решения системы дифференциальных уравнений в частных производных, описывающих структуру полупроводниковых приборов?

4. От чего зависит точность решения дискретизованной системы, описывающей структуру полупроводниковых приборов?

5. Какие основные алгоритмы используются для дискретизации базовых уравнений при численном моделировании полупроводниковых приборов?

6. Проиллюстрируйте вид сетки и схему дискретизации для метода конечных разностей.

7. Как выглядит сетка при использовании метода конечных элементов?

8. Чему равно значение функции внутри элемента для треугольных и для прямоугольных элементов?

9. Чему равен коэффициент усиления ошибки для функции y(x)?

10. От каких факторов зависит сходимость численного решения базовых дифференциальных уравнений для моделирования полупроводниковых приборов?