§ 3. Экономические задачи, содержащие матрицы и системы.

Ранее были приведены наиболее простые примеры экономических задач. Рассмотрим более конкретные модели.

В соответствии с многоотраслевой моделью Леонтьева, соотношения баланса в матричной форме могут быть представлены следующим образом:

или

,

где - вектор валового продукта, - вектор конечного продукта, - матрица прямых затрат. При этом матрица

называется матрицей полных затрат и матрица называется продуктивной, если все элементы матрицы положительны.

Основная задача межотраслевого баланса состоит в нахождении такого вектора валового выпуска , который при известной матрице прямых затрат обеспечивает заданный вектор конечного продукта , т.е.

.

При этом вектором чистой продукцией некоторой отрасли называется разность между вектором валовой продукцией этой отрасли и затратами продукции всех отраслей на производство этой отрасли - вектором . Данный вектор вычисляется как сумма по столбцам (строкам) матрицы межотраслевых поставок , каждый элемент которой, в свою очередь, равен .

Существует также обратная задача – если задана матрица межотраслевых поставок нескольких отраслей и вектор чистой продукции , то матрица прямых затрат может быть найдена в два этапа:

1) найти вектор валовой продукции как сумму вектора чистой продукции и суммы по столбцам (строкам) матрицы межотраслевых поставок: ;

2) найти коэффициенты матрицы прямых затрат как .

Более сложной может показаться задача, связанная с линейной моделью обмена (моделью международной торговли). В этом случае изначально задается структурная матрица торговли , где каждый элемент матрицы отражает долю национального дохода, которую страна тратит на покупку товаров у страны , причем сумма всех элементов в каждой строке . Необходимо или найти соотношение национальных доходов стран для сбалансированной торговли, или, если известен суммарный доход стран, равновесный вектор национальных доходов.

Для решения данной задачи необходимо решить уравнение вида

или

относительно вектора . Данное уравнение можно переписать в виде системы

,

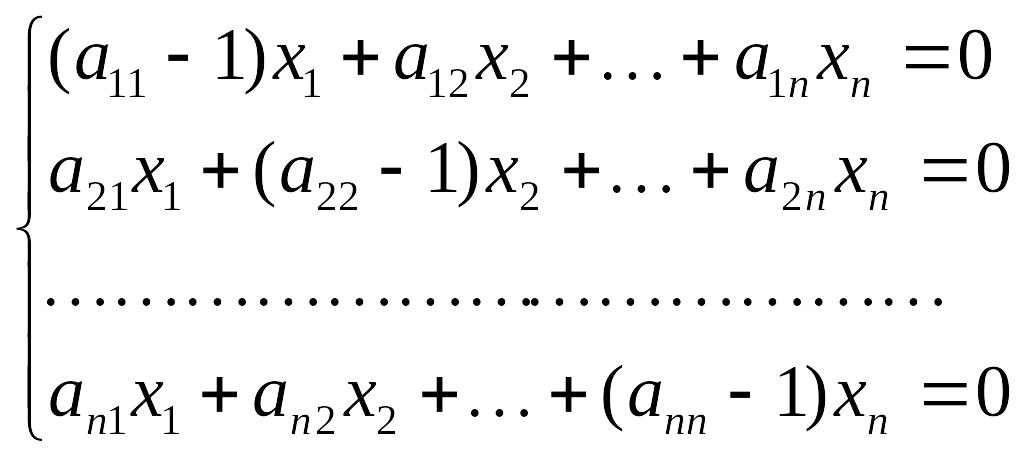которая называется однородной – правая часть каждого из уравнений равна нулю. Подобные системы принято решать методом Гаусса, причем решение в данном случае не будет единственным – см. пример 4 параграфа 2. Параметр, от которого будет зависеть найденное решение, можно найти, если задан суммарный доход стран. В противном случае, параметр в окончательном ответе можно вынести за скобку, тем самым, определив лишь соотношение национальных доходов стран для сбалансированной торговли.

Рассмотрим ряд конкретных примеров.

Пример 1. Выяснить, является ли продуктивной матрица прямых затрат трехотраслевой экономической системы:

и в случае положительного ответа составить межотраслевой баланс, если вектор конечной продукции .

Решение:

1) Вычислим матрицу полных затрат . Для нашего примера

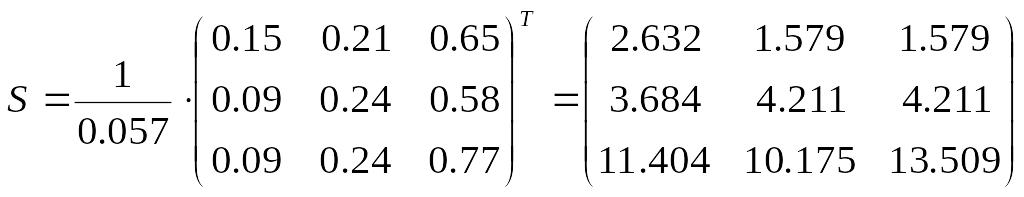
2) Вычислим вектор валовой продукции . Для нашего примера

3) Вычислим матрицу межотраслевых поставок . Для нашего примера

и т.д. Окончательно,

4) Вычислим вектор затрат продукции всех отраслей на производство -ой отрасли (как сумму всех элементов в каждом столбце).

Окончательно,

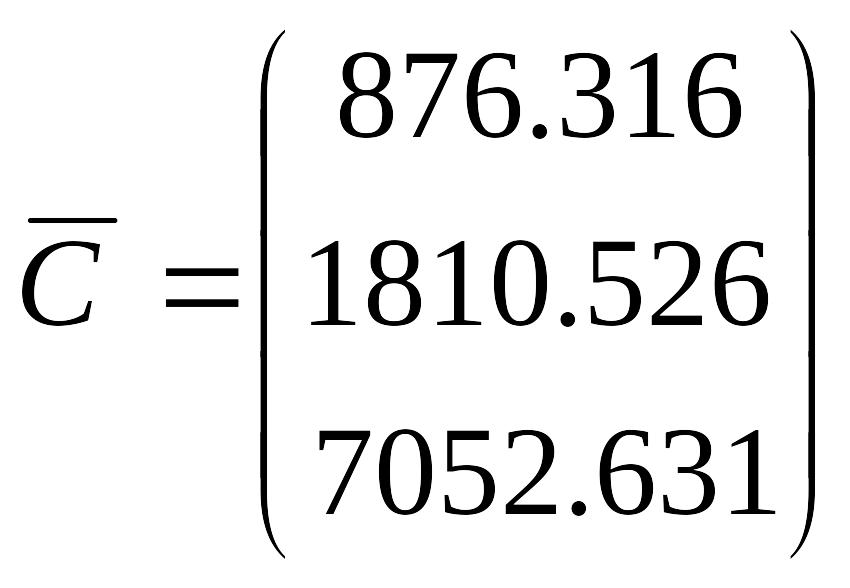
5) Вычислим вектор чистой продукцией :

6) Таким образом, работу данной системы можно представить следующей таблицей:

Отрасль		Потребление			Конечный продукт
		I	II	III
Производство	I	194.74	678.95	0	100
	II	97.37	0	2115.79	50
	III	584.21	1131.56	4936.84	400
Валовой продукт		973.68	2263.16	7052.63
Чистый продукт		97.37	432.63	0

Пример 2. Потребление одной из отраслей трехотраслевой системы зависит от некоторого изменяемого параметра. Установить, при каких положительных значениях параметра матрица прямых затрат данной системы будет являться продуктивной:

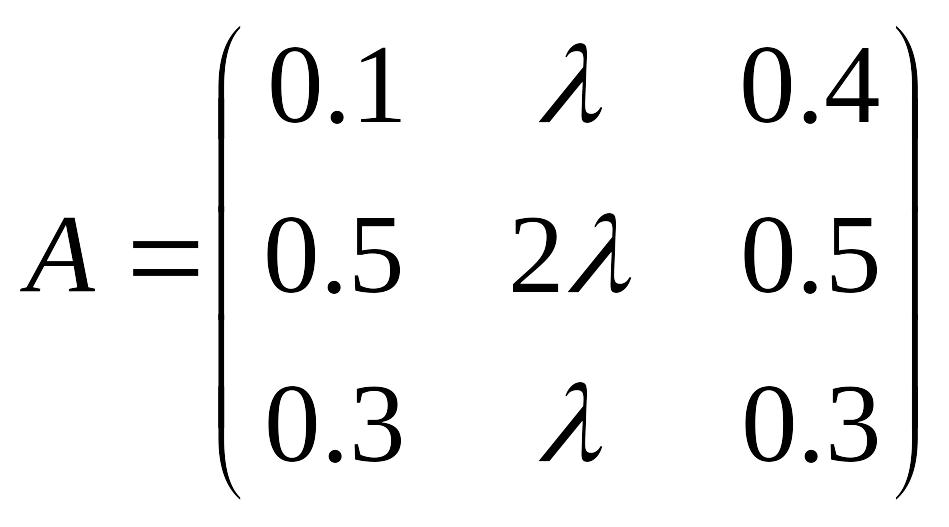
Решение:

Найдем матрицу полных затрат:

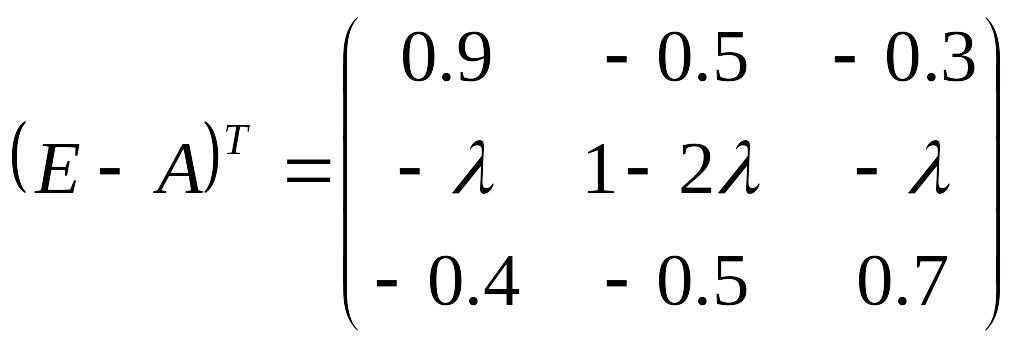
По определению, все элементы данной матрицы должны быть положительны. Для этого необходимо выполнение ряда условий:

или, следовательно,

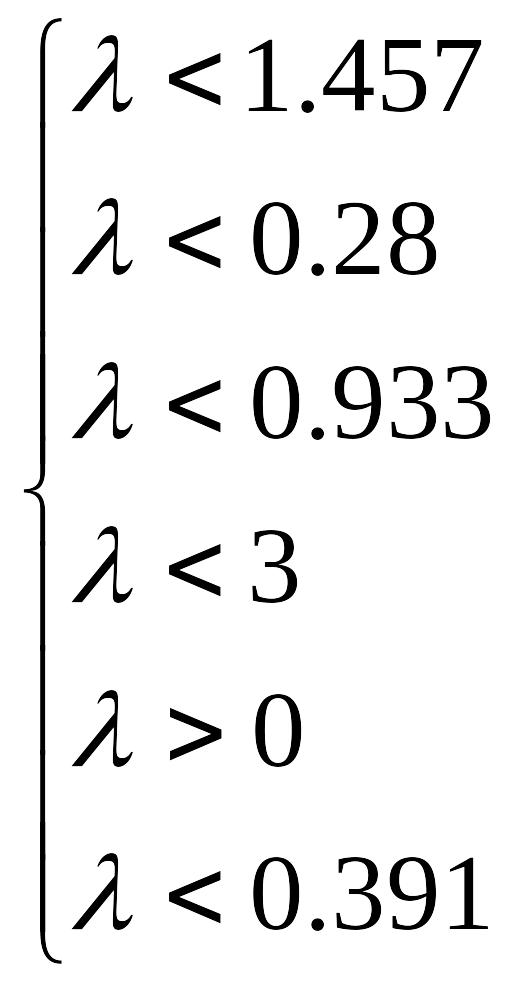
Из всех перечисленных условий вытекает, что матрица прямых затрат будет продуктивной при условии, что параметр

Пример 3. Имеются данные о работе системы нескольких отраслей в прошлом периоде и план выпуска конечной продукции в будущем периоде (в усл. ден. ед.). Найти матрицы прямых и полных затрат⁶.

Отрасль	Потребление		Чистая продукция
	I	II
I	100	160	240
II	275	40	85

Решение:

Сначала вычислим вектор валовой продукции (см. соответствующую теорию на стр. ?)

.

Полученные данные можно занести в таблицу следующим образом:

Отрасль	Потребление		Чистая продукция
	I	II
I	100	160	240
II	275	40	85
Валовой продукт	500	400

Для нахождения матрицы прямых затрат необходимо разделить каждый элемент матрицы на соответствующее число в строке валового продукта:

, ,

,

Тогда

и, соответственно,

.

Если есть возможность решить данную задачу на MathCadе, то сначала необходимо задать исходную матрицу и вектор , счетчики и по строкам и столбцам, затем ввести формулы для вычисления вектора , а затем матриц и . После чего просто вывести полученные результаты на экран. Это можно реализовать следующим образом:

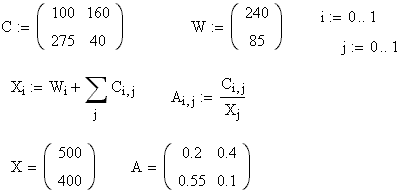
Здесь предумышленно не приводится вычисление матрицы полных затрат . Это предлагается выполнить самостоятельно, на основании примеров, рассмотренных ранее.

Пример 4. Найти соотношение национальных доходов 4 стран для сбалансированной торговли, если задана структурная матрица торговли⁷:

Решение:

Запишем однородную систему, необходимую для решения данной задачи:

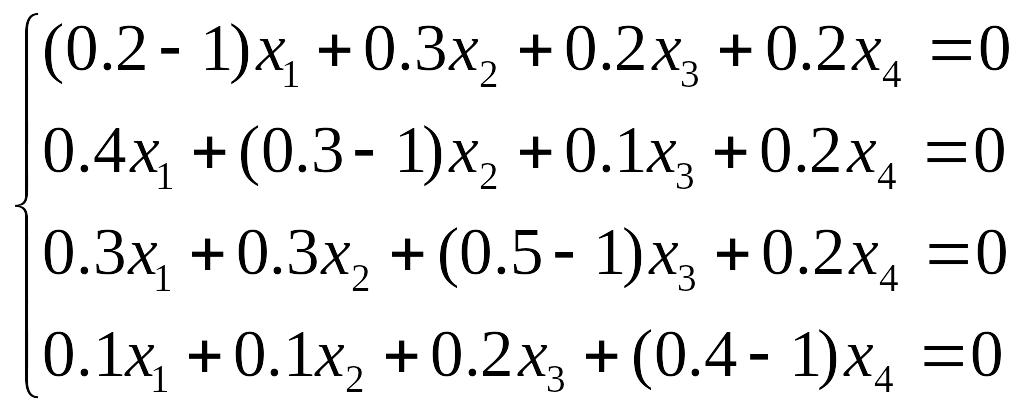
Вычисляя выражения в скобках, перейдем к записи, удобной для применения метода Гаусса. Далее, поменяв местами первую и последнюю строки и домножив каждую строку на 10 для удобства вычислений, получаем:

Получим нули в первом столбце (см. теорию и примеры по методу Гаусса на стр. ), после чего прибавим к последней строке вторую:

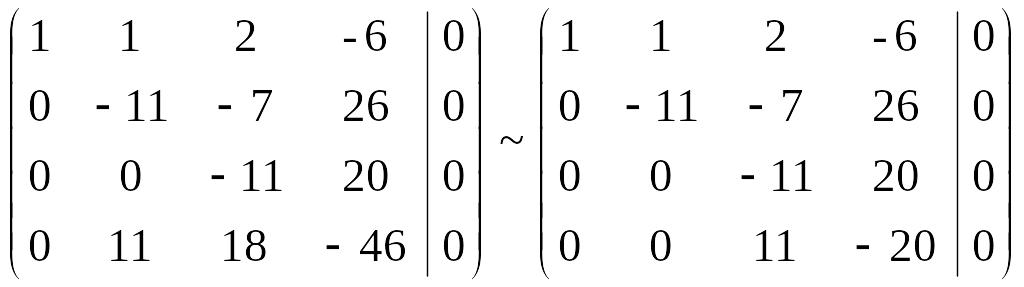
Прибавляя к последней строке третью, получаем нулевую строку, т.е., как уже было сказано ранее, система имеет множество решений. Вернемся к записи в виде системы.

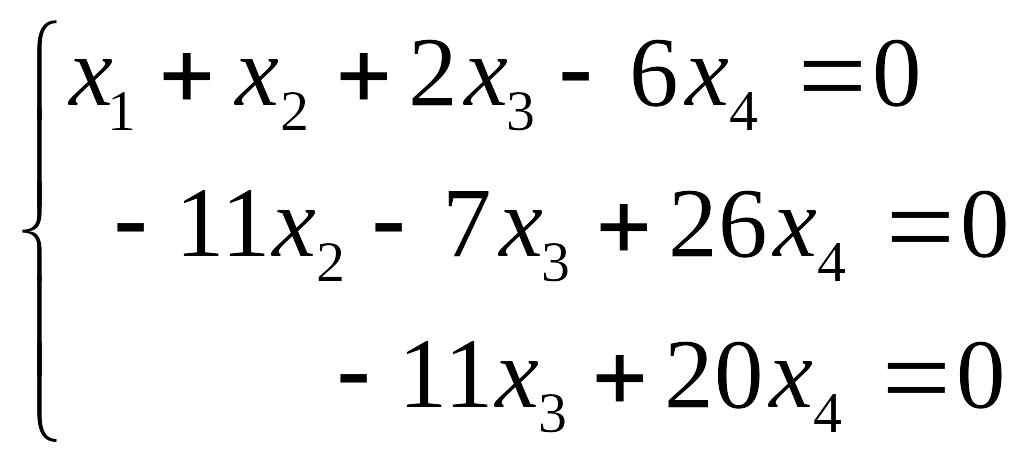
Пусть переменная равна некоторому параметру . Тогда

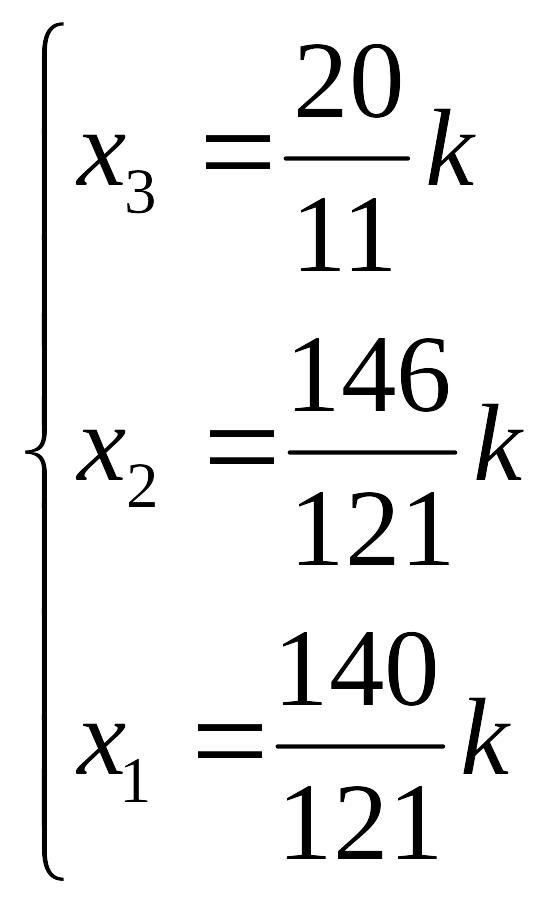
Иными словами, вектор национальных доходов стран имеет вид

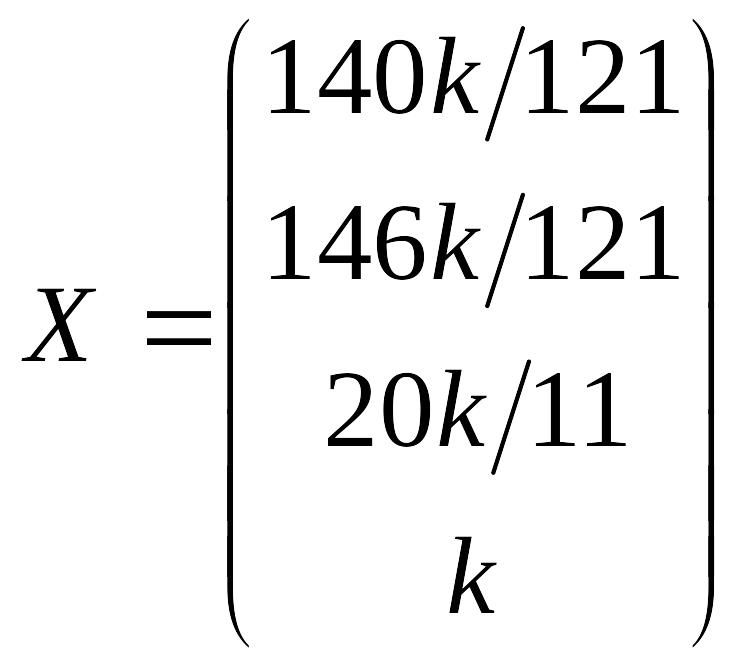
Полученный результат можно записать и в виде соотношения полученных четырех чисел. Для удобства записи домножим каждый элемент вектора на 121 и разделим на , тогда окончательное соотношение будет иметь следующий вид:

,

что и будет являться ответом к задаче.

Пример 5. Найти равновесный вектор национальных доходов в модели международной торговли, если задана структурная матрица торговли , а суммарный доход стран равен 402 усл. ед.⁸

Решение:

Запишем однородную систему, необходимую для решения данной задачи:

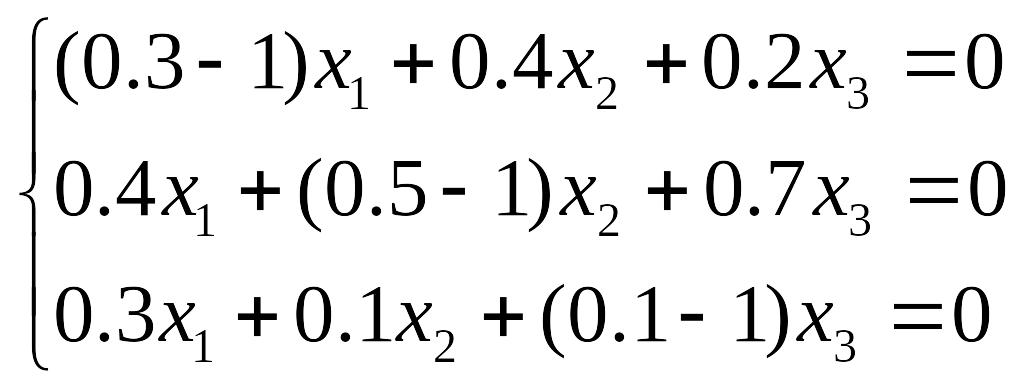
Вычисляя выражения в скобках, перейдем к записи, удобной для применения метода Гаусса. Далее, вычитая из второй строки третью и поменяв местами новую вторую строку и первую, домножаем каждую строку на 10 для удобства вычислений. Получаем:

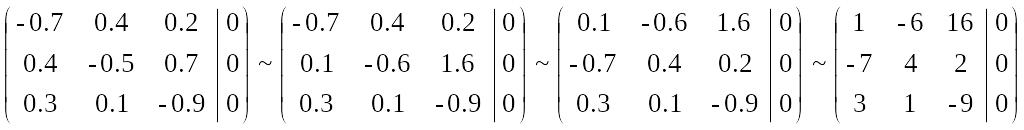Получим нули в первом столбце (см. теорию и примеры по методу Гаусса на стр. ):

Домножая последнюю строку на 2 и прибавляя ко второй, получаем нулевую строку. После чего, разделив третью строку на 19, окончательно получаем:

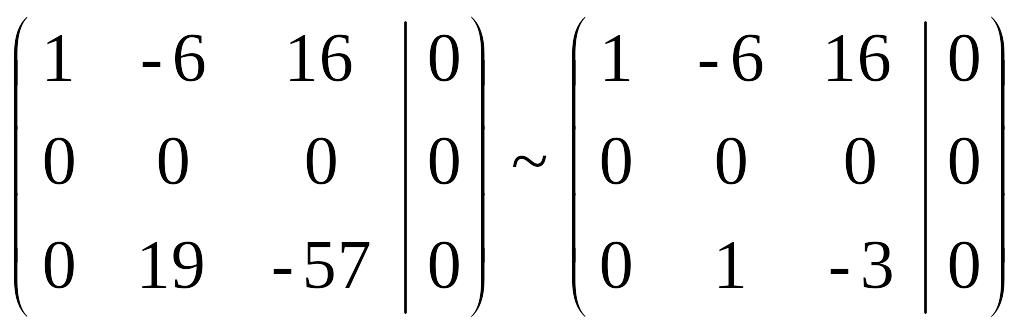
Возвращаясь к записи в виде системы:

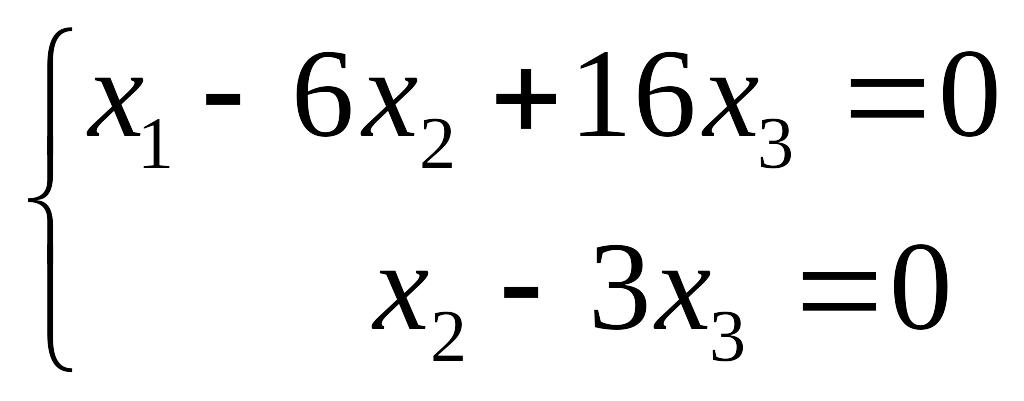
Пусть , тогда

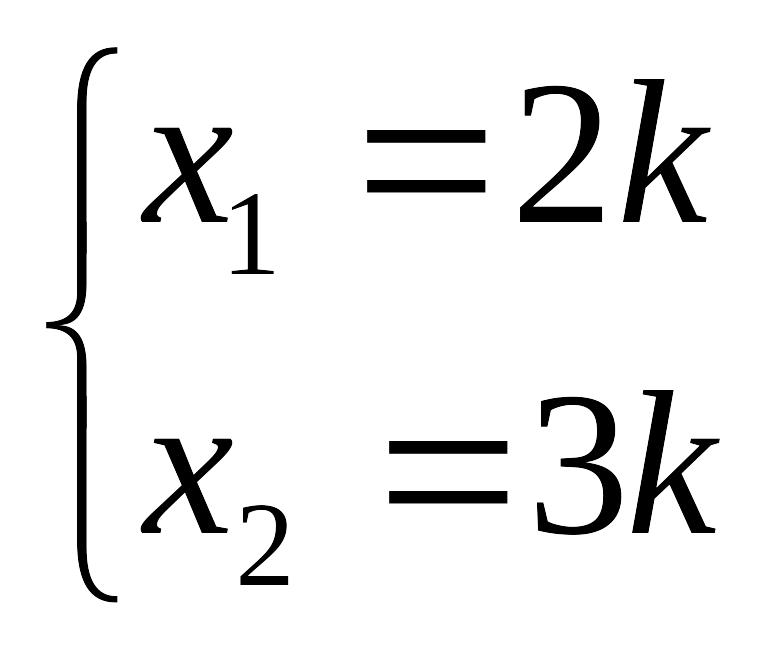
Таким образом, вектор национальных доходов в данной модели имеет вид:

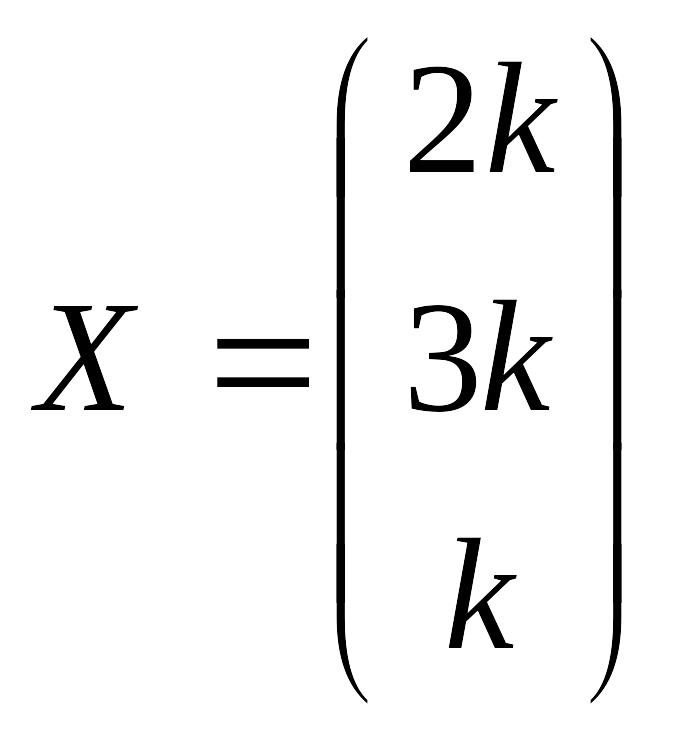
Поскольку известно, что суммарный доход стран равен 402 усл. ед., то это означает, что , откуда . Таким образом, подставляя вычисленное значение в полученный выше результат, окончательно получаем, что для сбалансированной торговли приведенных в модели стран необходимо, чтобы доход первой страны равнялся , доход второй страны и доход третьей страны .