1.3. Решение систем линейных алгебраических уравнений.

Рассмотрим систему линейных алгебраических уравнений следующего вида:

,

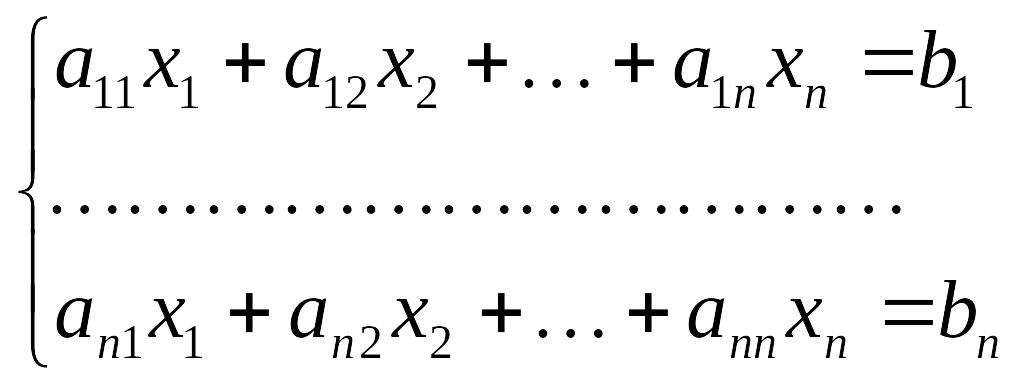где , а также - некоторые числа, а - неизвестные величины, которые необходимо найти. Задачи такого типа достаточно часто возникают в экономической теории.

Два метода, наиболее часто применяемые для решения систем такого вида, при условии, что порядок их невелик - это метод Крамера и матричный метод (в некоторой литературе он называется методом обратной матрицы). В случае, если система имеет 4-й порядок и более, чаще всего применяют метод Гаусса – см. § 2.1.

И в том, и в другом методе, система изначально представляется в виде

,

где , , .

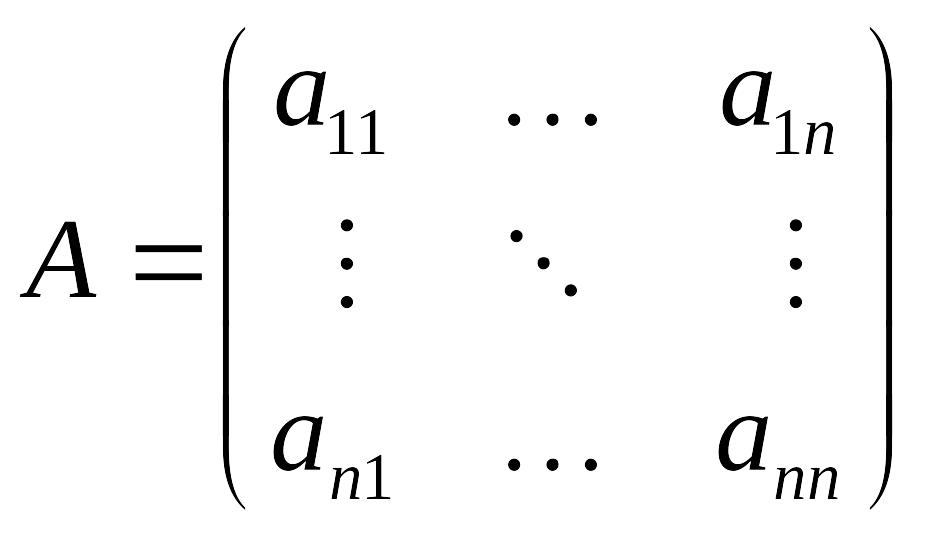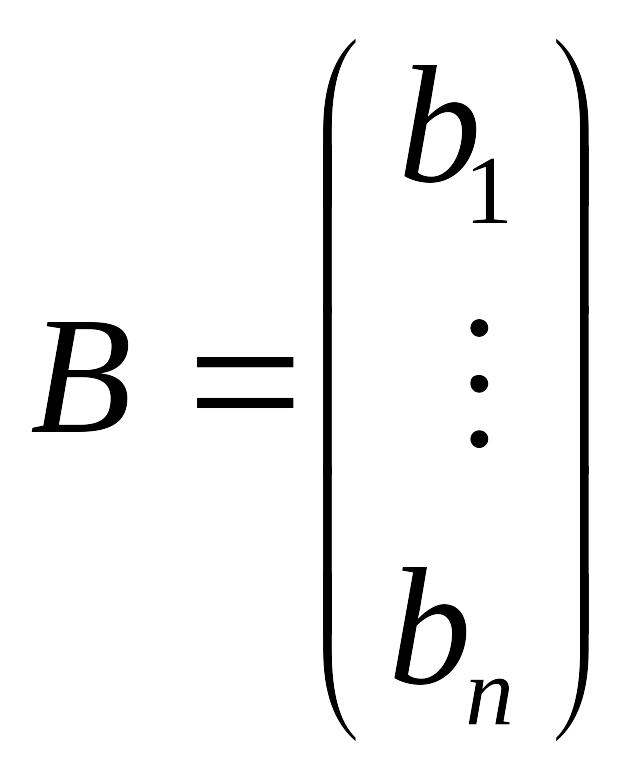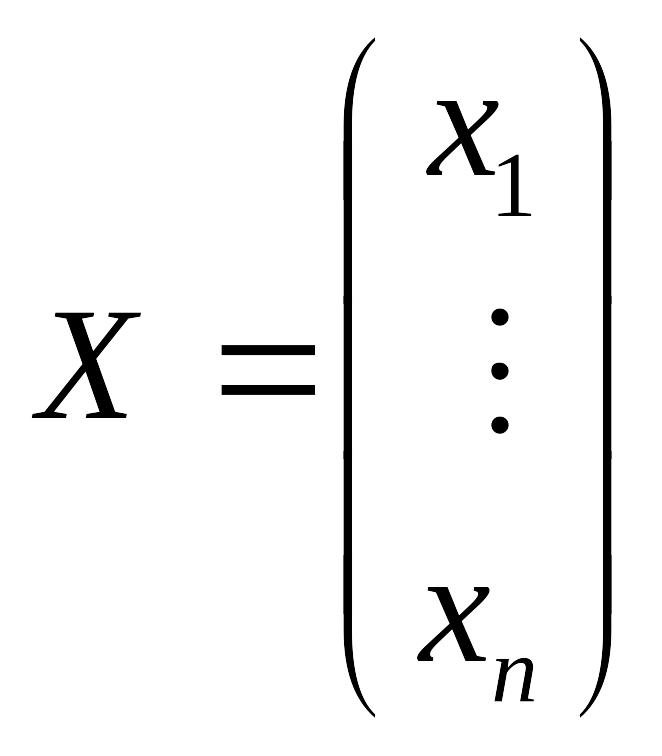Метод Крамера заключается в последовательном нахождении определителя:

,

,

, …,

.

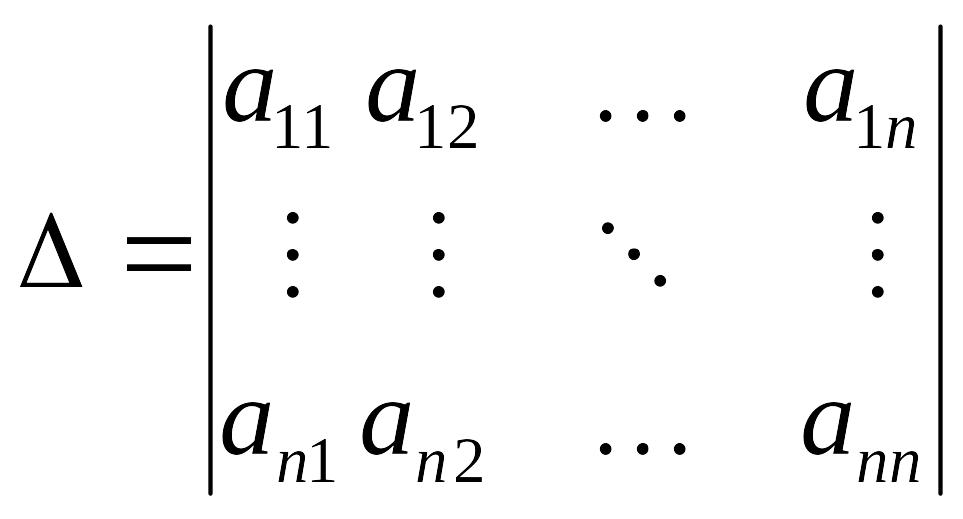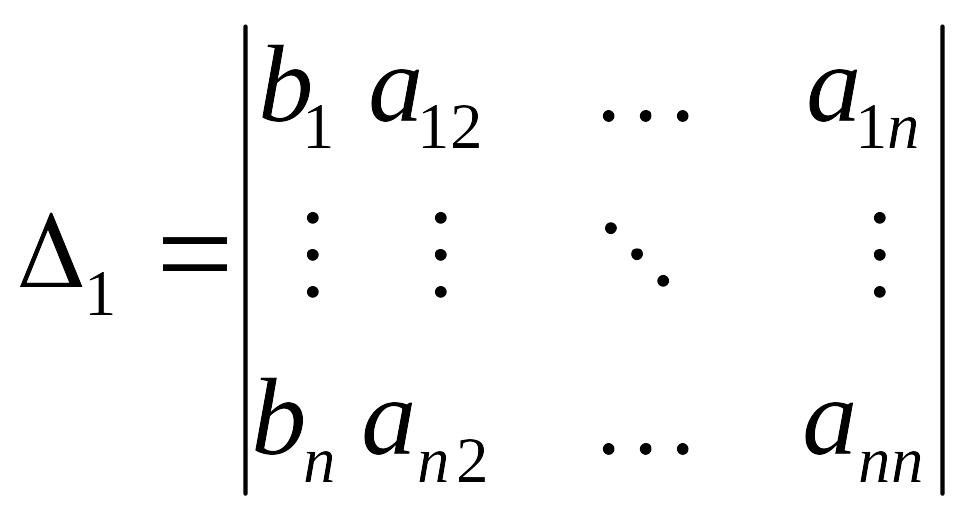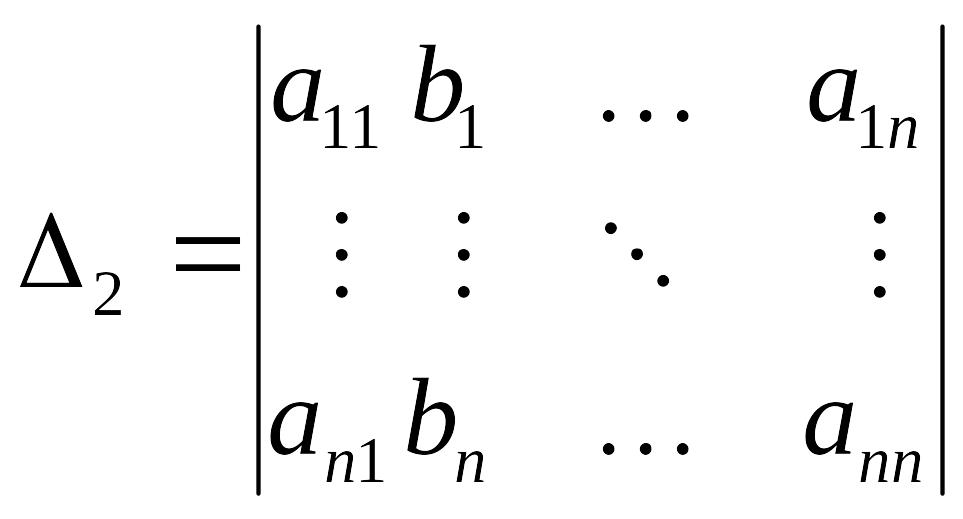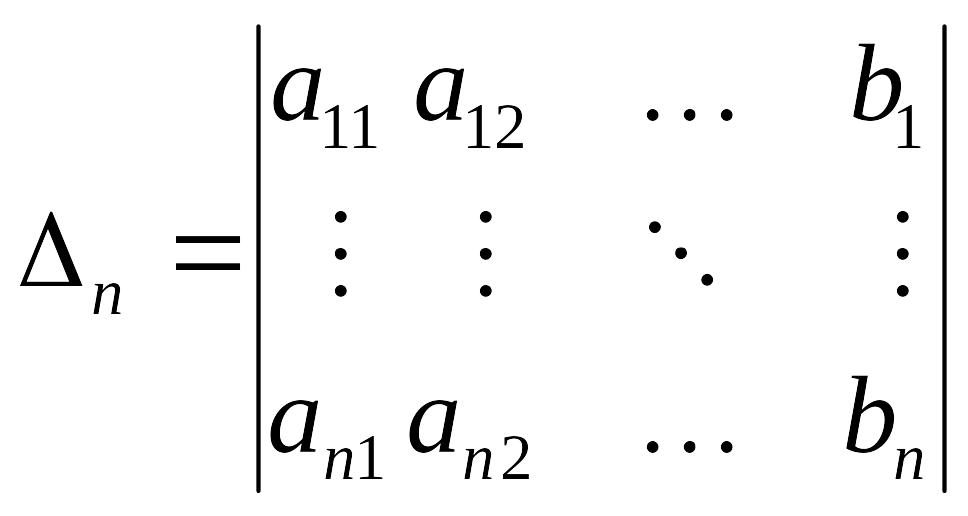Тогда решение системы может быть найдено по формулам:

, , …, .

Метод обратной матрицы заключается в вычислении матрицы , обратной к матрице и последующем вычислении вектора неизвестных как

Рассмотрим несколько примеров.

Пример 19. Решить систему методом Крамера:

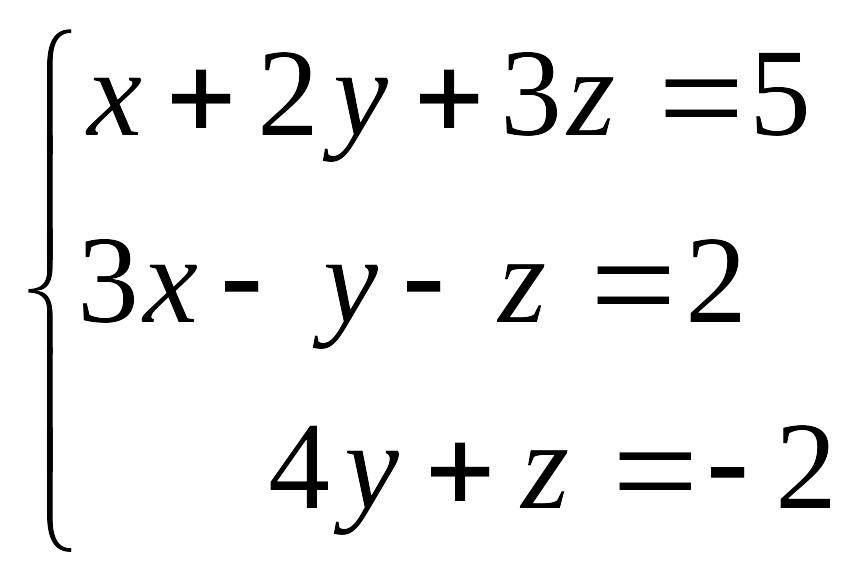
Для решения данной системы методом Крамера необходимо вычислить 4 определителя третьего порядка:

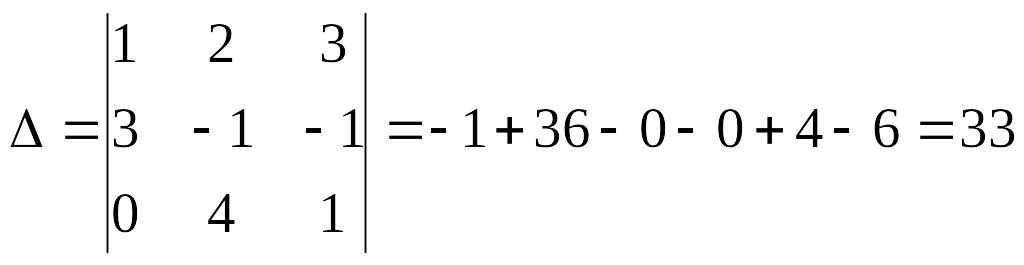
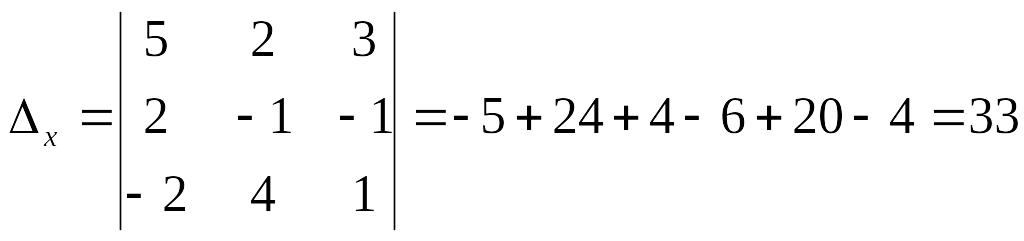
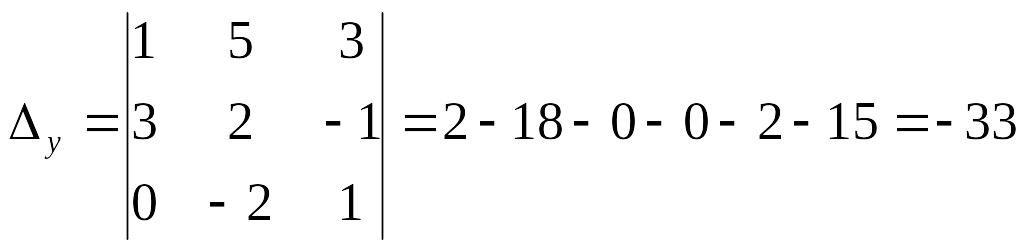
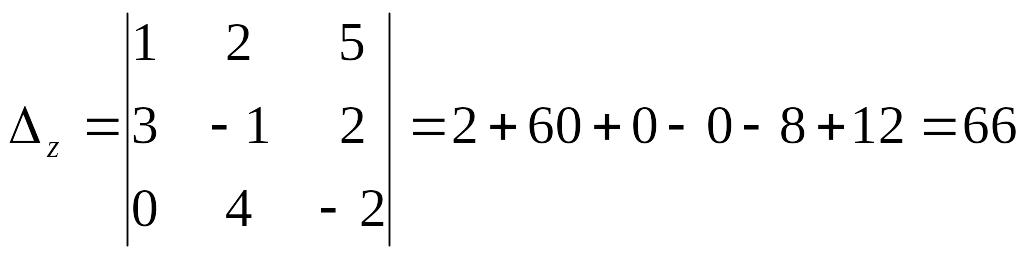
Тогда окончательный ответ:

,

,

.

Пример 20. Решить систему методом обратной матрицы:

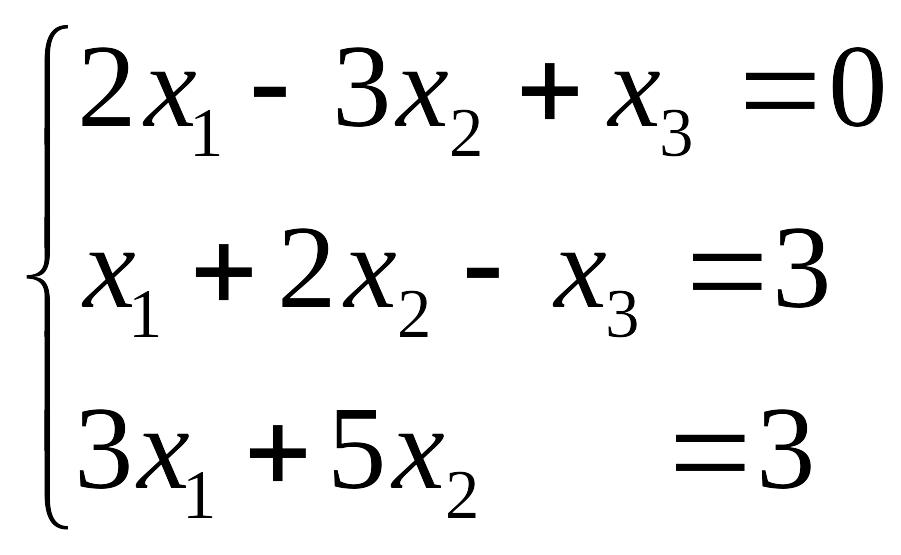
В данной системе

, .

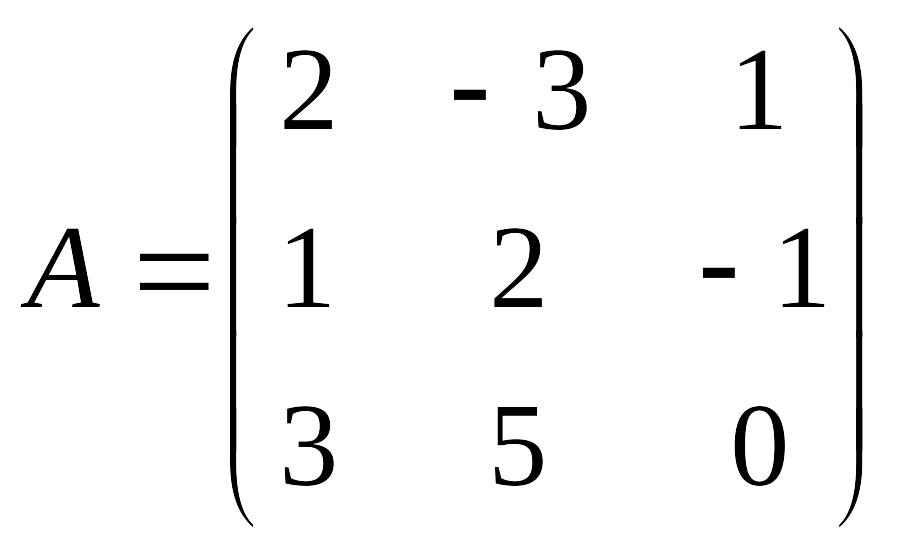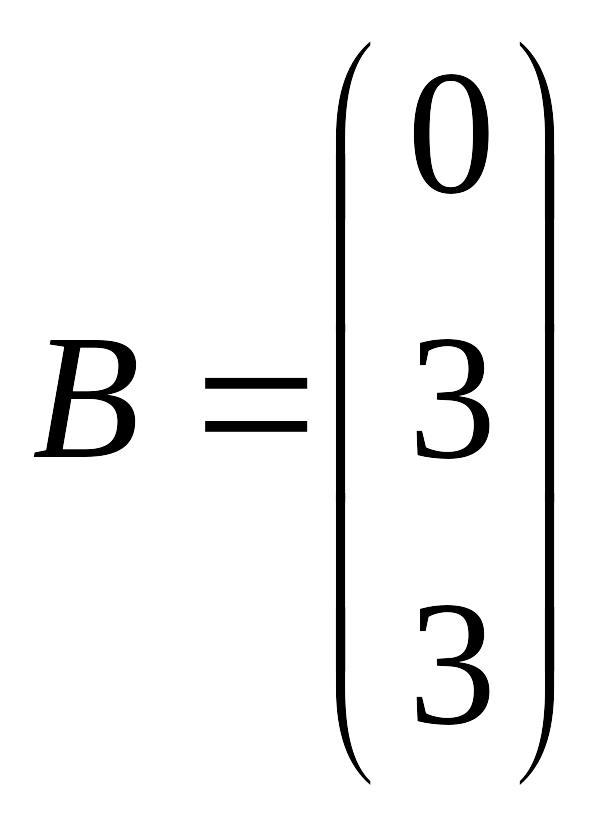Найдем матрицу, обратную к матрице в соответствии с приведенным ранее алгоритмом.

1)

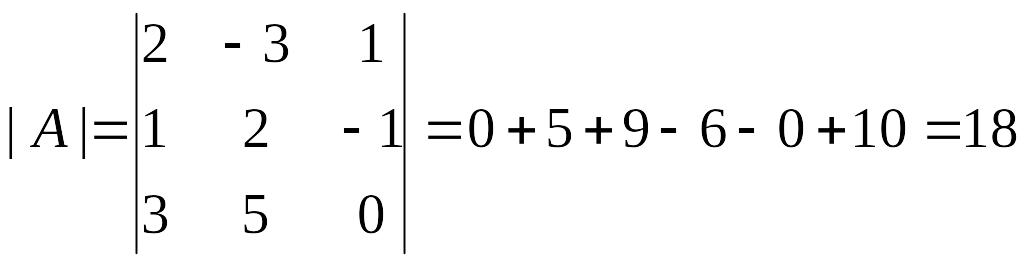
2)

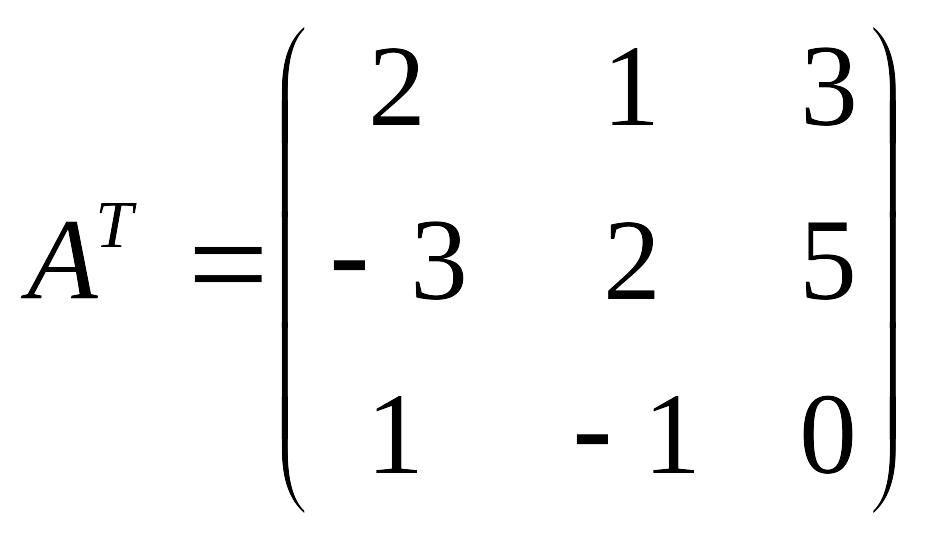
3)

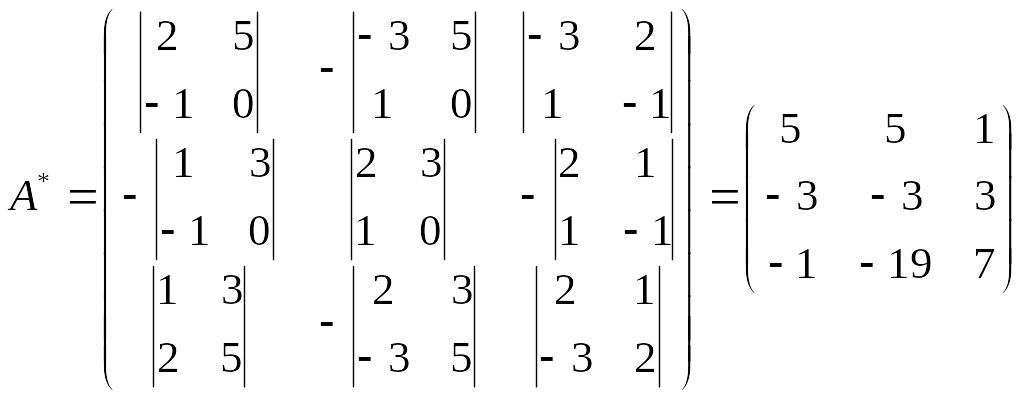
4)

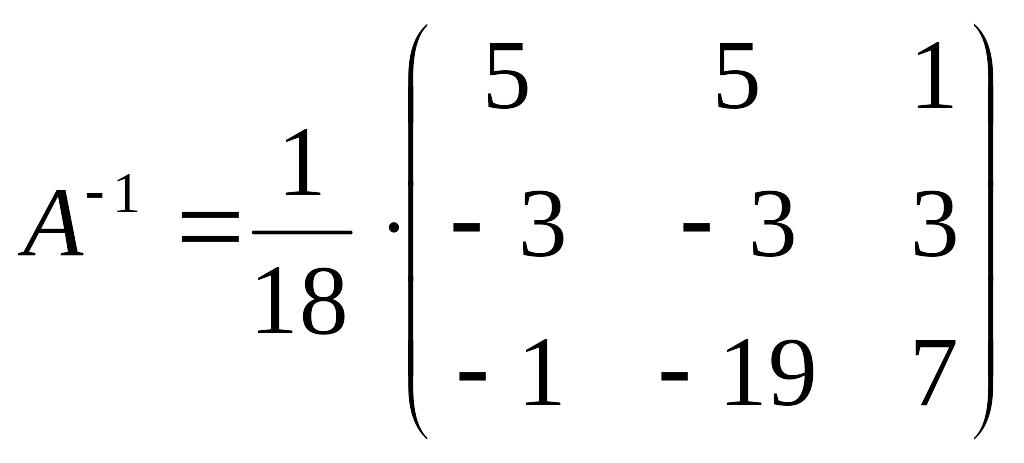
Тогда решение системы

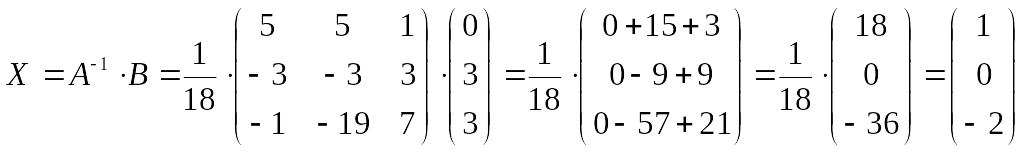
Пример 21. Решить систему методом Крамера, результат проверить методом обратной матрицы.

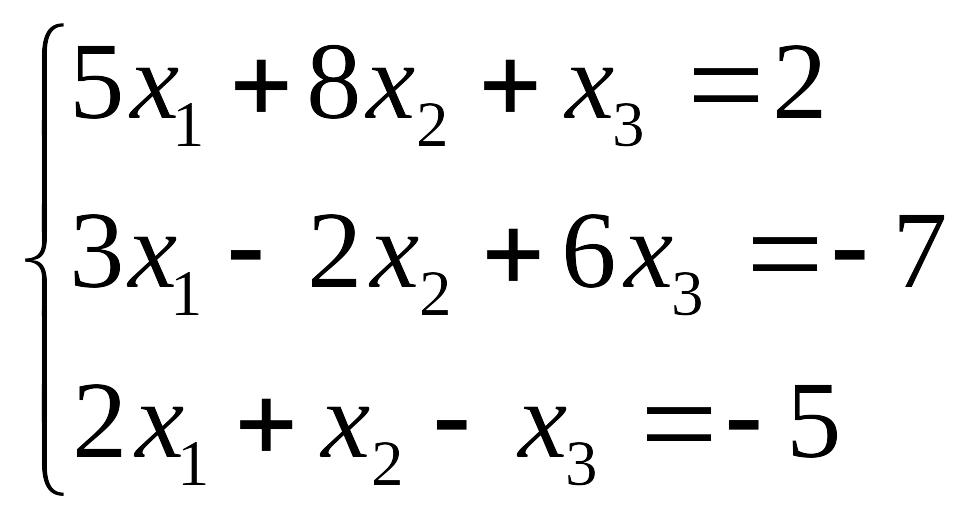
Решим данную систему методом Крамера:

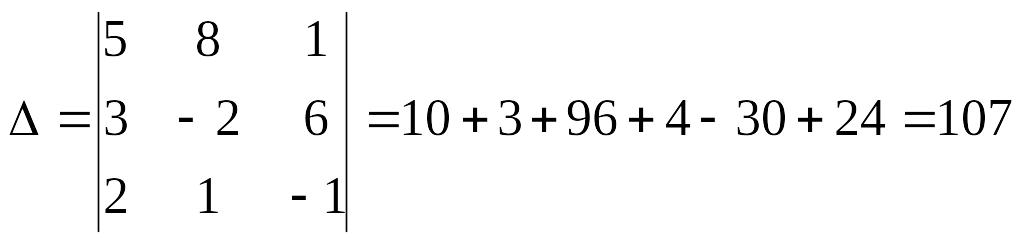
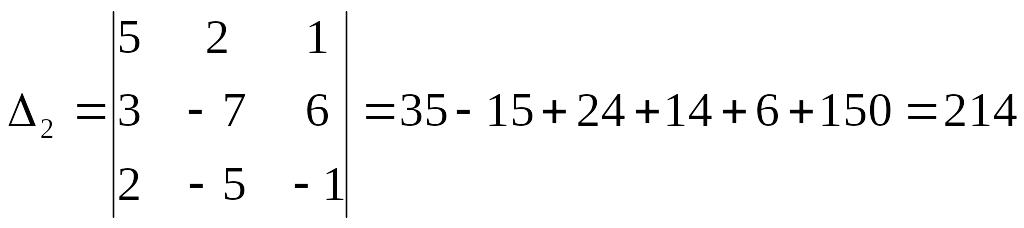
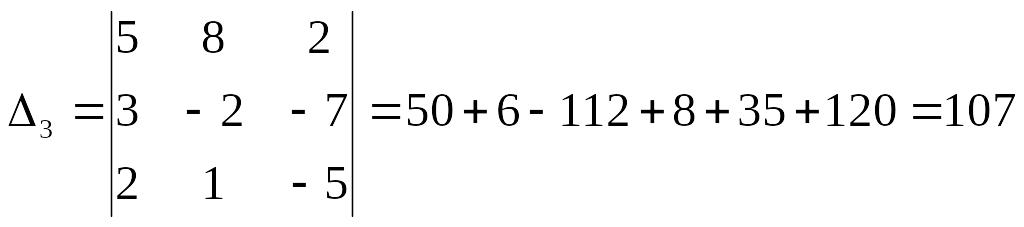
Тогда окончательный ответ:

,

,

.

Решим данную систему методом обратной матрицы. Найдем матрицу, обратную к матрице в соответствии с приведенным ранее алгоритмом.

1) - найдено в ходе метода Крамера.

2)

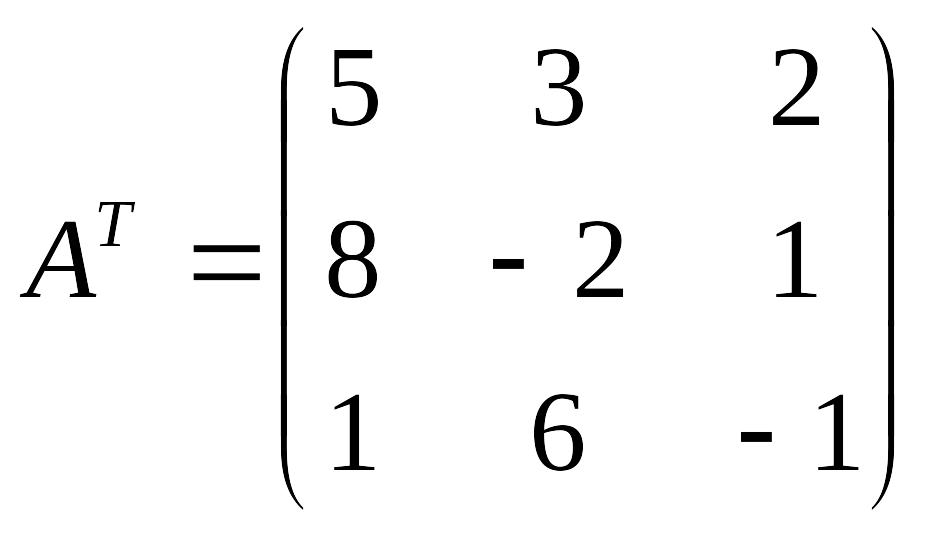
3)

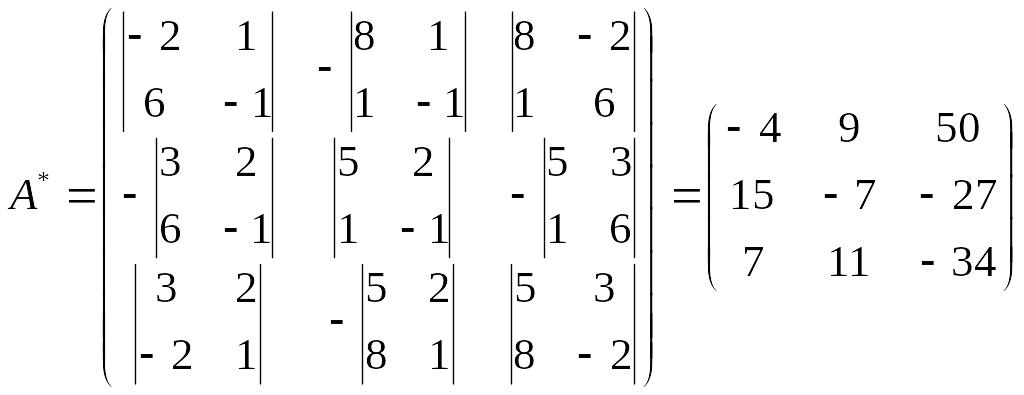
4)

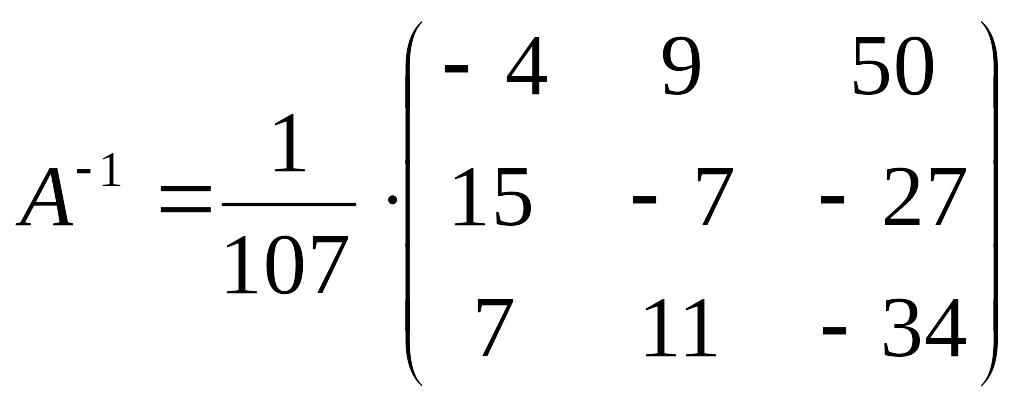
Тогда решение системы

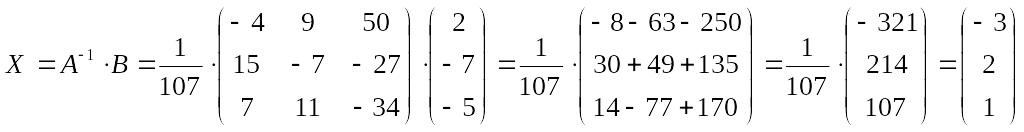
1.4. Примеры для самопроверки. § 2. Метод Гаусса. Лемма Ахо.

2.1. Общая теория и примеры.

Метод Гаусса заключается в последовательном исключении всех коэффициентов матрицы, лежащих ниже и выше главной диагонали. При этом все элементарные преобразования ведутся только по строкам. Прямой ход Гаусса заключается в получении нулей ниже главной диагонали, преобразования ведутся сверху вниз и слева направо. Обратный ход Гаусса заключается в получении нулей выше главной диагонали и преобразования ведутся снизу вверх и справа налево.

Метод Гаусса целесообразно использовать для вычисления определителей и обращения матриц старше третьего порядка, решения систем уравнений с большим числом неизвестных, а также систем с неединственным решением.

Однако, при строгом соблюдении всех правил классического алгоритма, достаточно часто возникают дробные значения, что не всегда удобно. Поэтому при аналитическом решении будем использовать некоторые допустимые преобразования, не соответствующие классическому алгоритму, но позволяющие получить решение с меньшими вычислительными проблемами.

Рассмотрим конкретные примеры.

Пример 1. Вычислить определитель:

Вычисления будут существенно проще, если в начале каждого последующего шага на главной диагонали удается получить единицу. В рассматриваемом примере на нулевом шаге это можно сделать, например, так: из четвертой строки вычесть третью, домноженную на 2, а затем поменять первую строку и новую четвертую местами.

Замечание 1. При замене строк местами перед определителем появиться знак минус (см. свойство определителя № 7).

Замечание 2. Физического изменения третьей строки не происходит, мы домножаем ее “в уме”, а реально изменится лишь четвертая, т.е. та, из которой мы вычитаем.

На первом шаге прямого хода с помощью элементарных преобразований получим нули в первом столбце ниже главной диагонали. При этом первую строку будем домножать (“в уме”! В дальнейшем этот факт не будет указываться каждый раз, но подразумевается, что умножение происходит именно так) на 4, на 3 и на 2 и, соответственно, вычитать полученный результат из второй, третьей и четвертой строк:

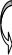
В течении всех последующих шагов прямого хода первая строка считается “замороженной” - не изменяется сама и не используется для преобразования других строк.

Перед началом второго шага получим единицу на главной диагонали во второй строке, например так: четвертую строку домножим на 3 и вычтем из третьей, после чего вторую и новую третью поменяем местами. При этом перед определителем появится еще один знак минус, т.е.

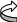
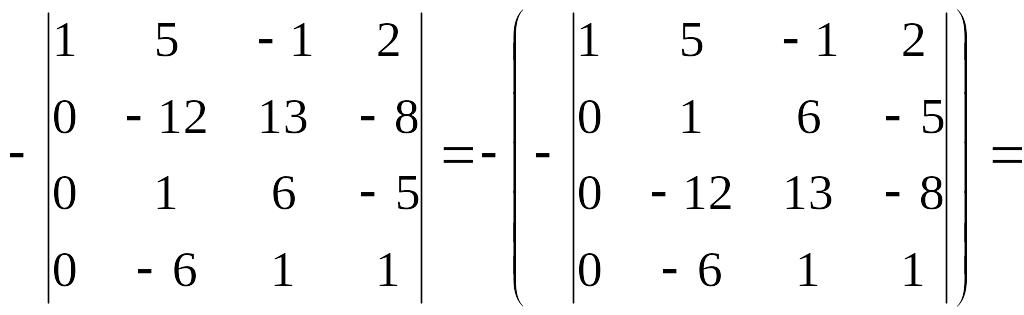
Заметим, что в данном конкретном примере получить 0 в третьей строке ниже главной диагонали можно несколько проще – домножить четвертую строку на 2 и вычесть из третьей. Для получения нуля в четвертой строке второго столбца домножим вторую строку на (- 6) и вычтем результат из четвертой:

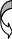
Теперь “замороженными” считаются уже две строки – первая и вторая. Продолжим преобразования: домножим третью строку на 3 и вычтем из четвертой:

,

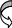
а затем из третьей вычтем четвертую, домноженную на 3:

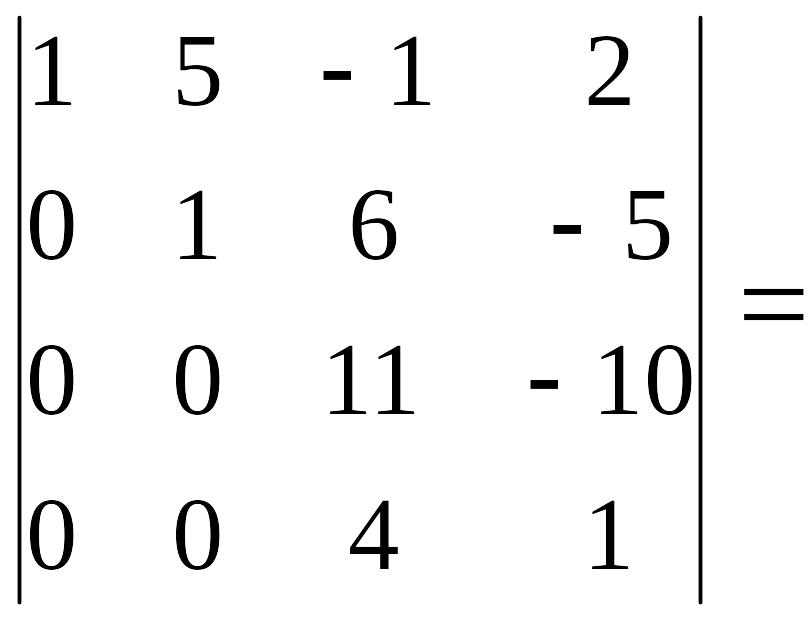
Последний штрих: из четвертой строки вычитаем третью, домноженную на (- 4). Окончательно получаем:

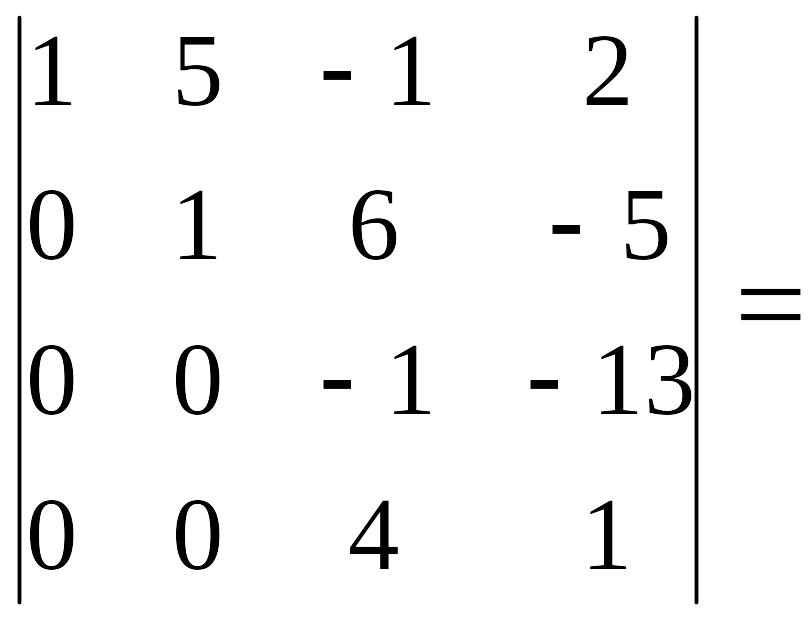
Обратный ход метода Гаусса (аналогичные действия для получения нулей выше главной диагонали) в данном случае можно не выполнять, т.к. в соответствии со свойством №3 определителя (см. § 1)

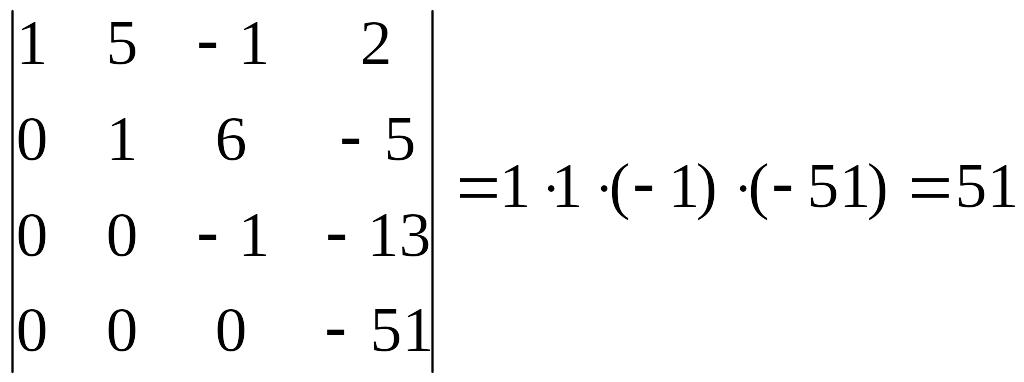
Пример 2. Решить систему:

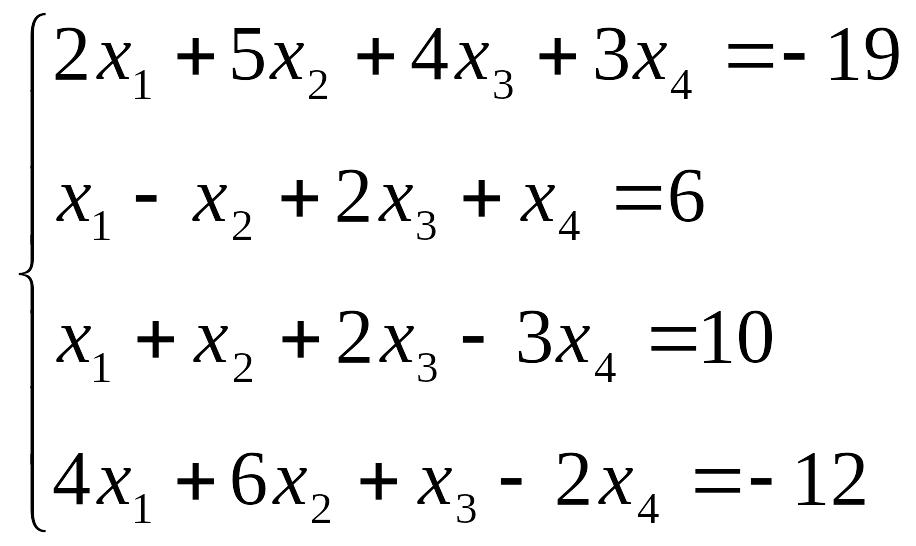
При решении систем линейных алгебраических уравнений строки матрицы можно менять местами, все знаки при этом остаются постоянными. Допустимо также деление всей строки расширенной матрицы на одно и то же число.

Запишем расширенную матрицу данной системы, а затем поменяем первую и вторую строку местами:

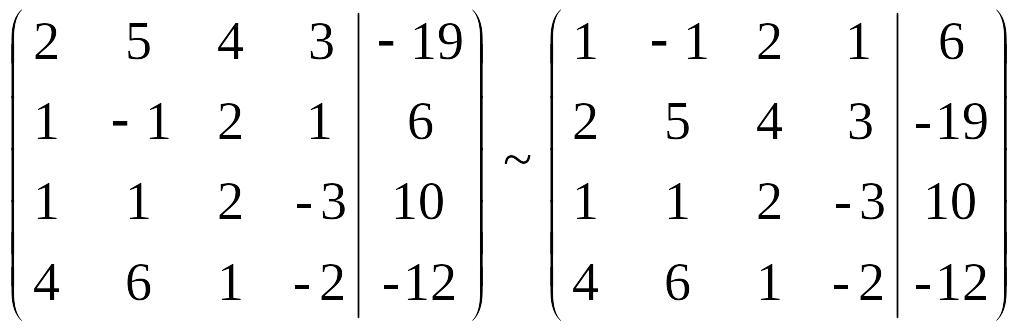
Принцип прямого хода аналогичен уже рассмотренному примеру. На первом шаге получим нули в первом столбце ниже главной диагонали. При этом первую строку будем домножать (“в уме”!) на 2, на 1 и на 4 и, соответственно, вычитать полученный результат из второй, третьей и четвертой строк:

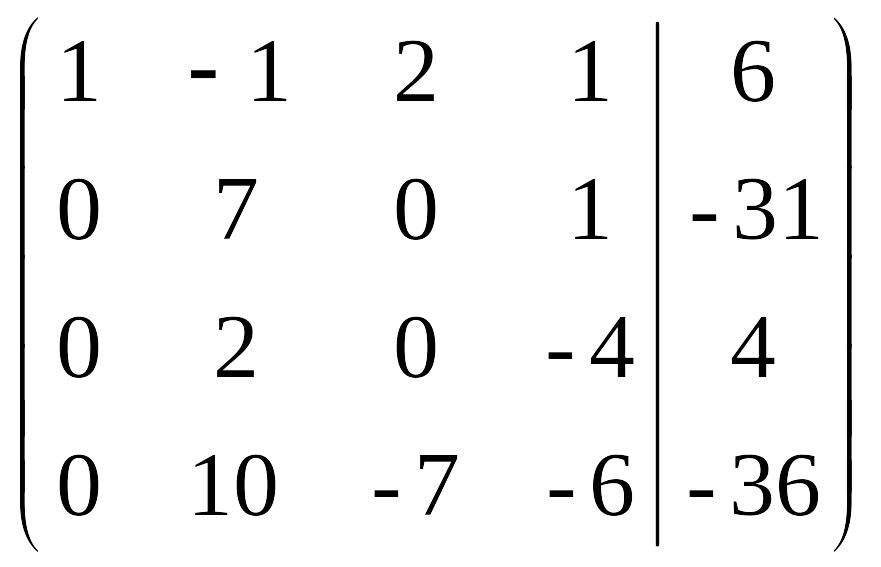
Поменяем местами вторую и третью строки, после чего разделим всю новую вторую строку на 2:

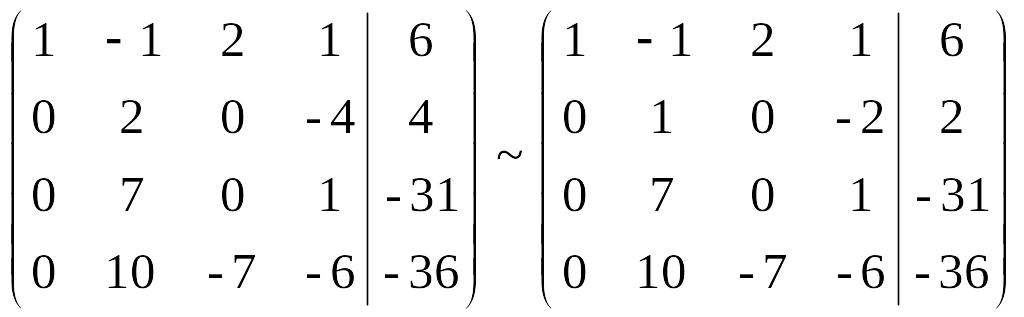
На втором шаге получим нули во втором столбце ниже главной диагонали. При этом вторую строку будем домножать на 7 и на 10 и, соответственно, вычитать полученный результат из третьей и четвертой строк:

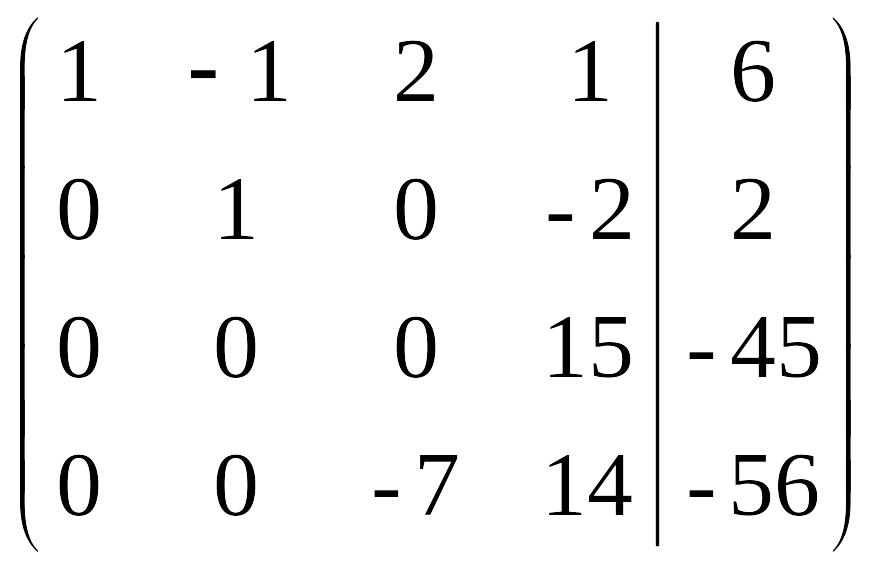
Поменяем местами третью и четвертую строки, а затем разделим их на (- 7) и 15 соответственно:

На этом прямой ход метода Гаусса закончен.

Во-первых, мы можем снова перейти к форме записи в виде системы

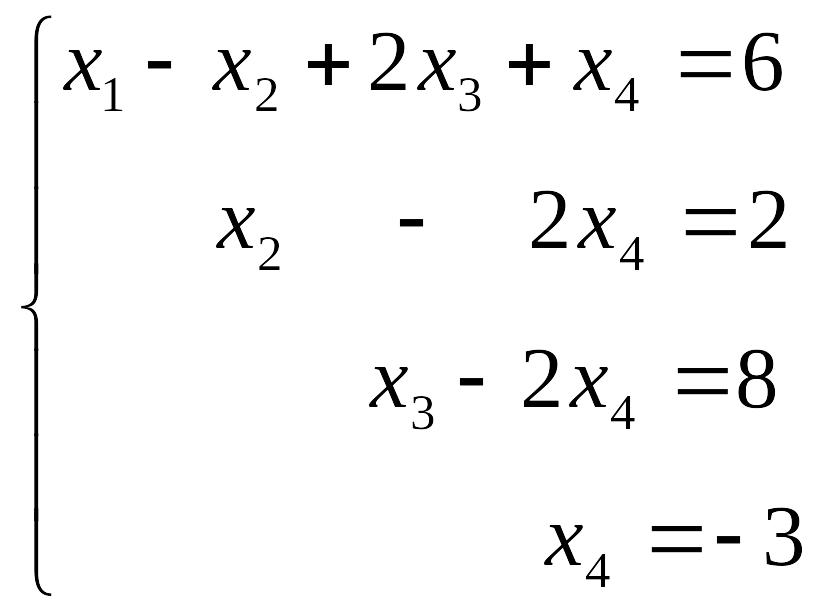
и дальше решать ее “школьным” способом – теперь это просто. Во-вторых, мы можем выполнить обратный ход метода Гаусса и получить то же самое решение. Мы уже знаем, что при этом преобразования ведутся снизу вверх и справа налево.

На первом шаге обратного хода получим нули выше главной диагонали в последнем столбце. Строки при этом “оттаивают” в обратном порядке, т.е. на первом шаге обратного хода можно осуществлять работу только с последней строкой. Будем домножать ее на (- 2), на (-2 ) и на 1 и, соответственно, вычитать полученный результат из третьей, второй и первой строк:

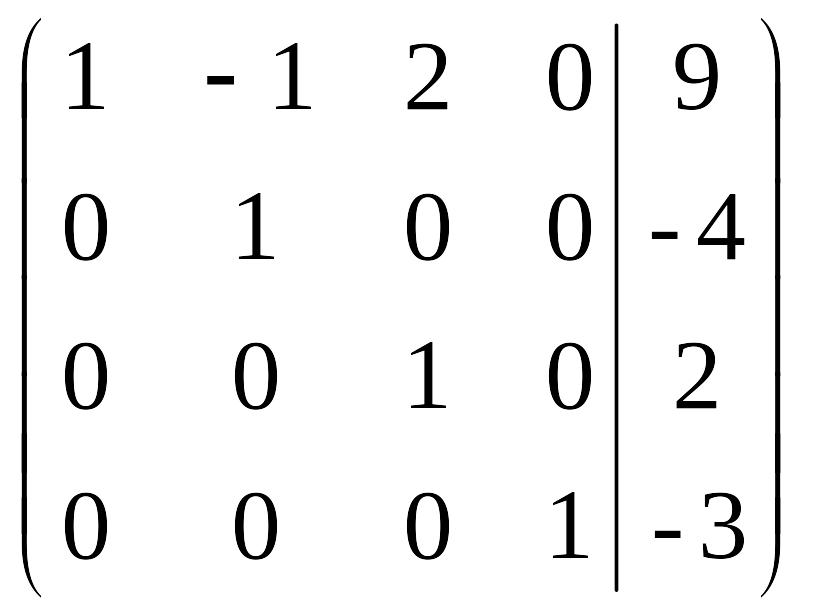
Аналогично получим нули в третьем столбце выше главной диагонали, учитывая при этом, что теперь “оттаяла” и третья строка. В данном конкретном примере вторая строка в изменениях не нуждается, поэтому всего лишь домножим третью строку на 2 и вычтем результат из первой:

Осталось получить ноль в первой строке во втором столбце. Домножим вторую строку на (- 1) и вычтем из первой:

Решением будут являться числа, отделенные вертикальной чертой:

, , , .

Пример 3. Решить систему:

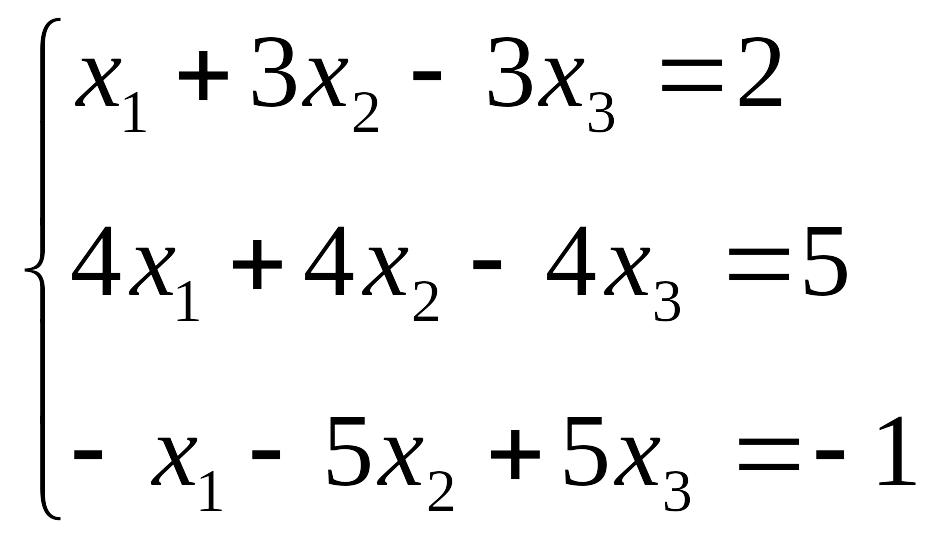
Если мы попробуем решить данную систему методом обратной матрицы (см. § 1), мы остановимся на этапе нахождения определителя - , т.е. обратной матрицы не существует. В этой ситуации возможны два варианта: или решений нет, или их бесконечно много. Но метод обратной матрицы не дает дальнейших результатов, мы даже не знаем, какой из этих двух вариантов представлен в данной системе.

Воспользуемся методом Гаусса. Ввиду того, что он уже был разобран достаточно подробно, лишние комментарии будут опущены.

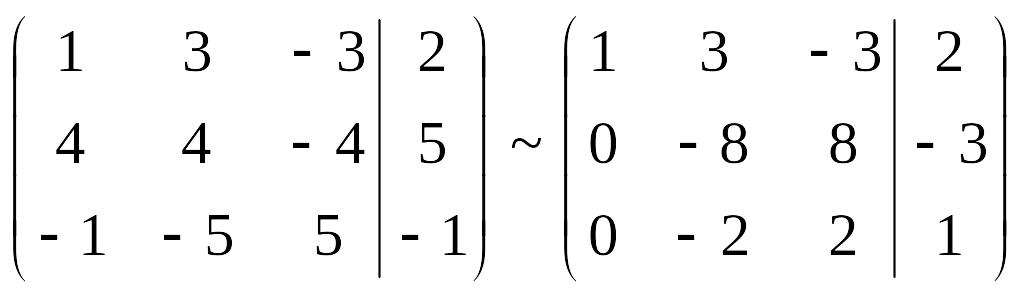
Домножим третью строку на 4 и вычтем из второй:

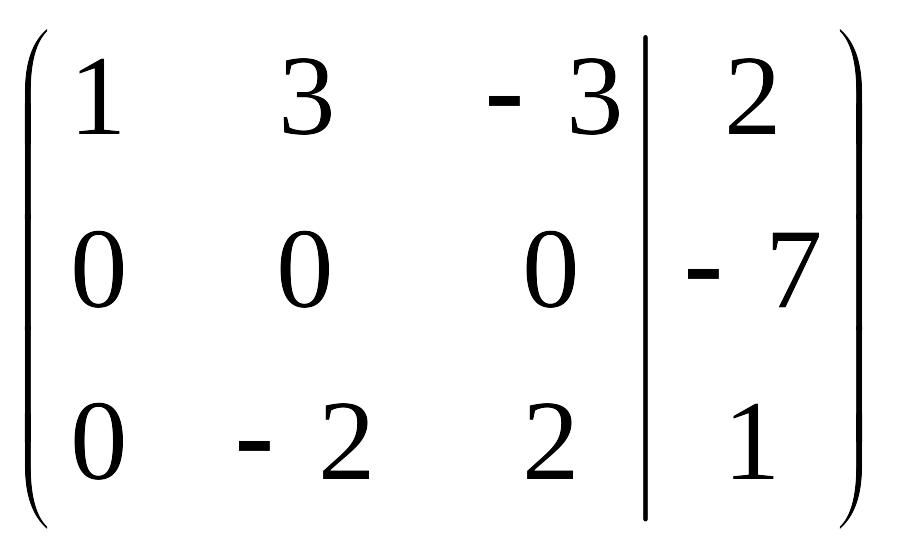
По своей сути последняя запись означает следующее:

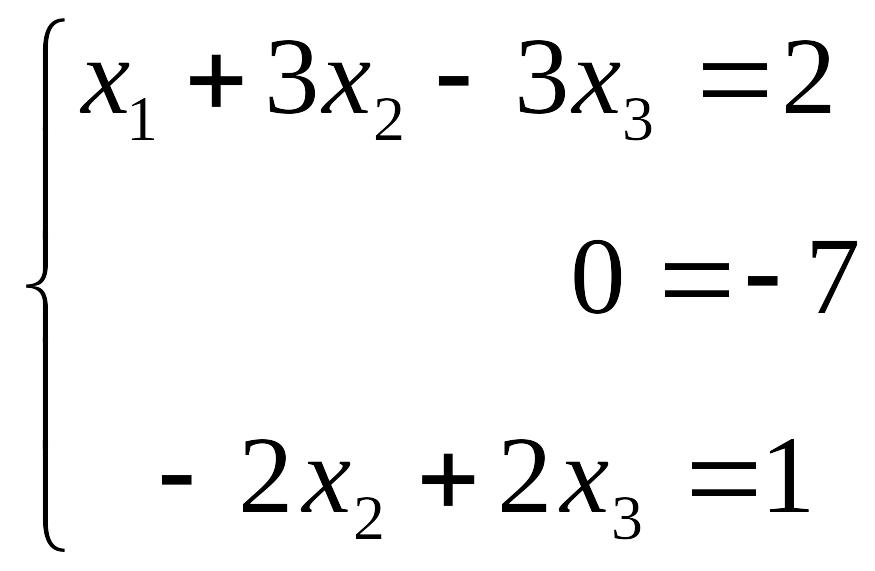
Вторая строка указывает нам на то, что данная система изначально противоречива – у нее не может быть решений!

Итак, если в ходе элементарных преобразований хотя бы одна строка является нулевой, но при этом после вертикальной черты содержит некоторое отличное от нуля число – система решений не имеет.

Пример 4. Решить систему:

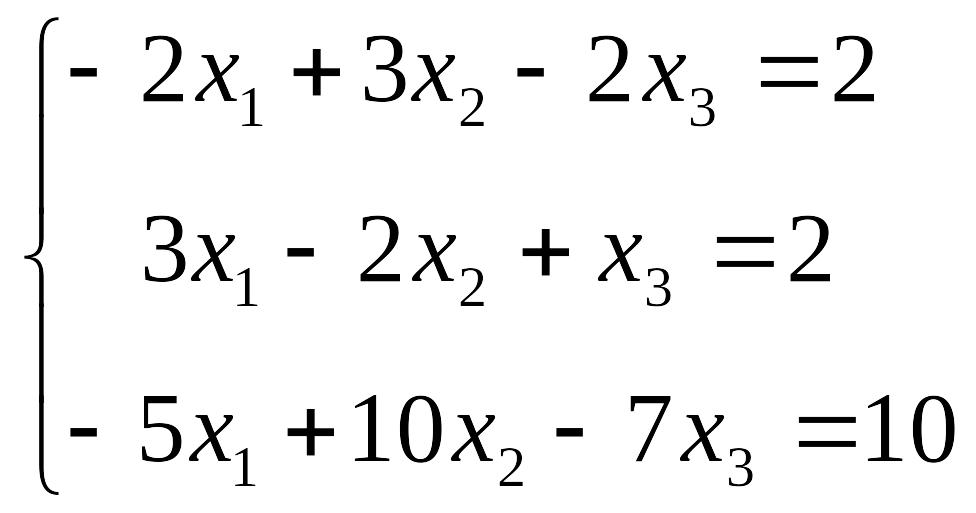
Определитель матрицы данной системы также равен нулю. Воспользуемся методом Гаусса. На нулевом шаге первую строку домножим на (- 1) и вычтем из второй. Затем поменяем эти строки местами.

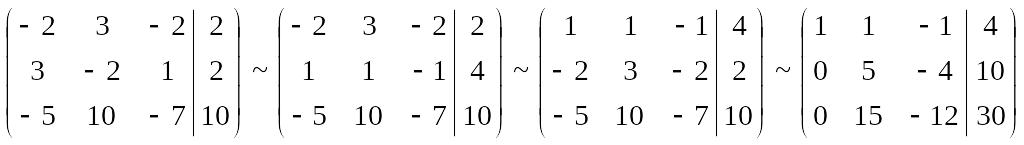
Домножим вторую строку на 3 и вычтем из третьей:

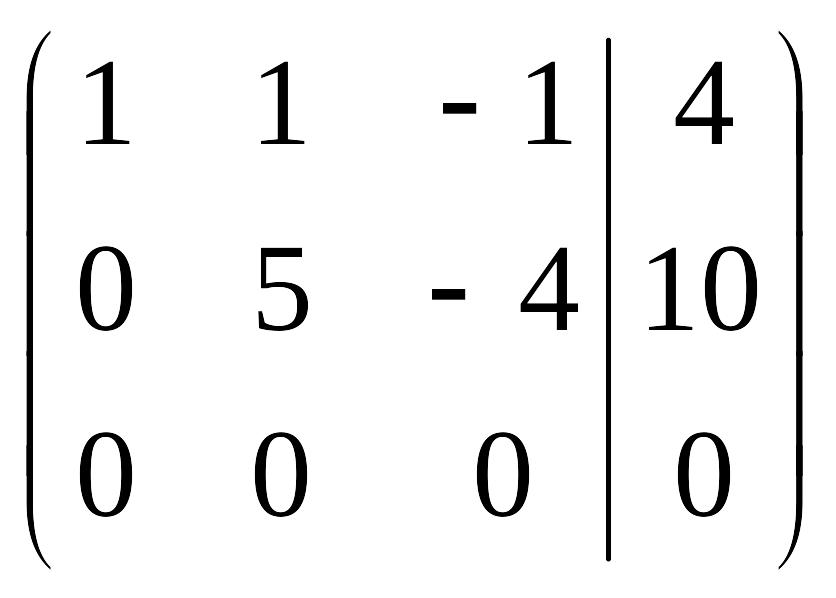
По своей сути эта запись означает следующее:

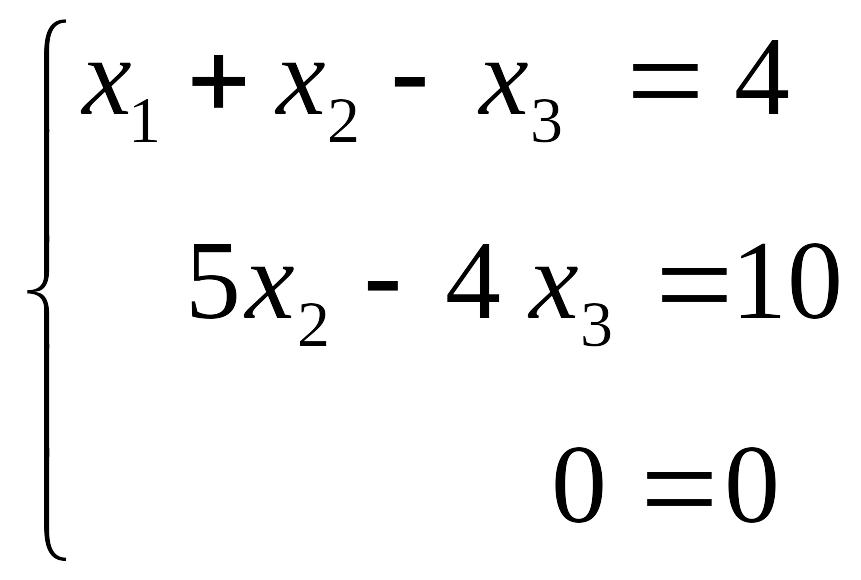
Данная система не противоречива, но ее решение не является единственным, что достаточно часто встречается в задачах с экономическим содержанием (см. параграф 3).

Пусть переменная - некоторый параметр , от которого будут зависеть переменные и . Тогда последняя запись системы примет вид

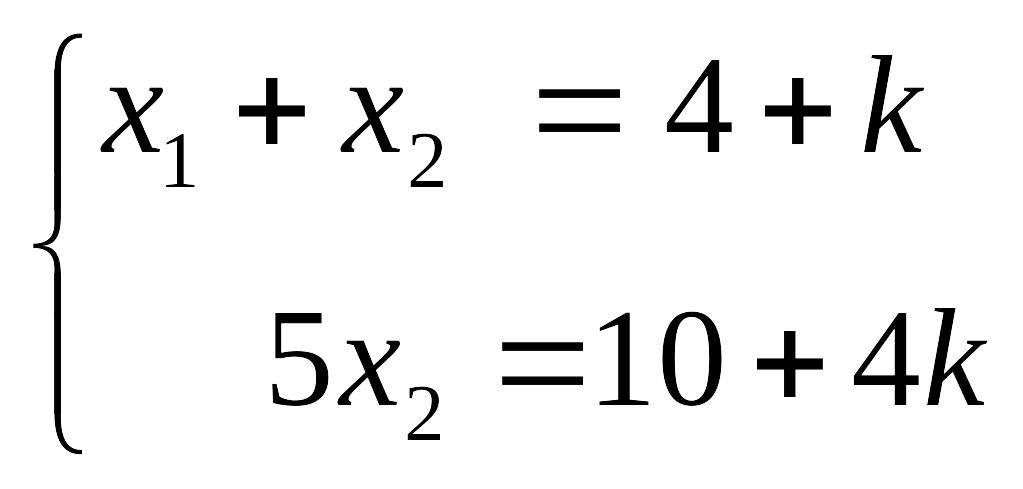
Решая данную систему, получаем:

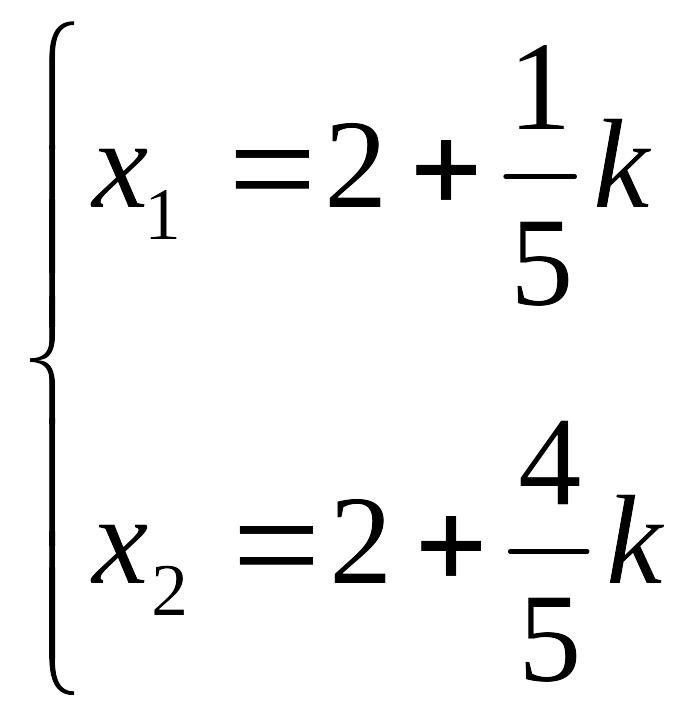
Если по каким-то соображениям параметр равен, например, 5, то, подставляя это значение в систему, получаем, что решением будет следующая тройка значений:

, , .

Если параметр равен 0, то решением будет следующая тройка:

, , .

Поскольку может быть фактически любым, число решений данной системы бесконечно.

Итак, если в ходе элементарных преобразований хотя бы одна строка является нулевой и при этом после вертикальной черты также содержится ноль – система имеет бесконечное множество решений.

Рассмотрим алгоритм вычисления матрицы, обратной к данной, основанный на методе Гаусса и являющийся достойной альтернативой классическому алгоритму, приведенному в § 1.2.

Известно, что если элементарные преобразования Гаусса выполнять над матрицей вида и после всех преобразований получить матрицу , то матрица является обратной к матрице .

Пример 5⁴. Вычислить матрицу, обратную к

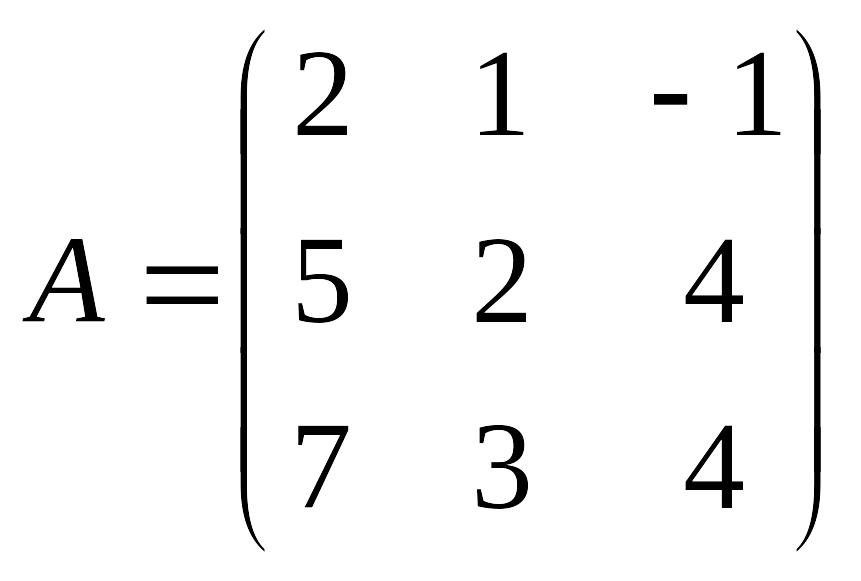
Запишем присоединенную матрицу

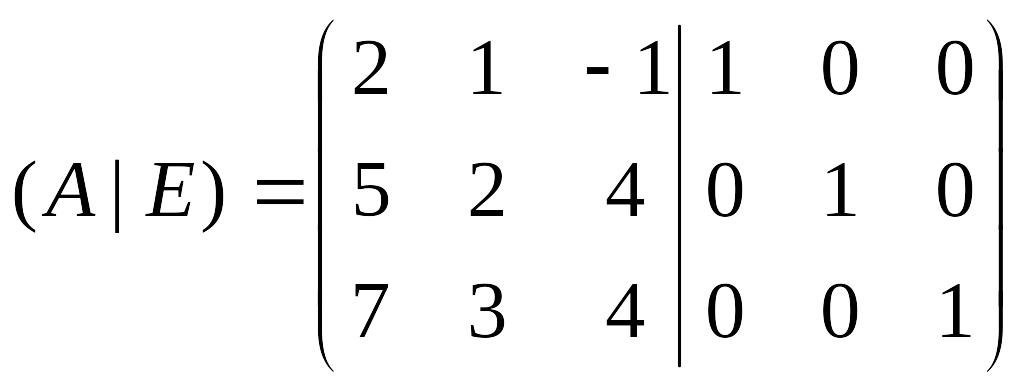
Из второй строки вычтем первую, домноженную на 2, а из третьей - первую, домноженную на 3. Получаем

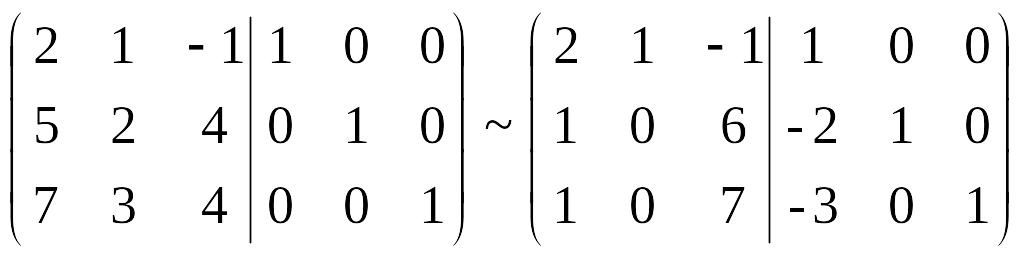
Запишем первую строку как третью. Затем из новой второй вычтем новую первую, а из новой третьей – новую первую, домноженную на 2.

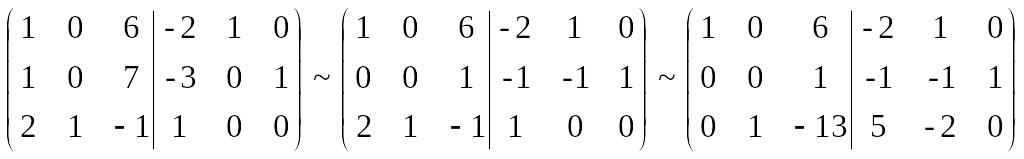
Поменяв местами вторую и третью строки, завершаем прямой ход метода Гаусса:

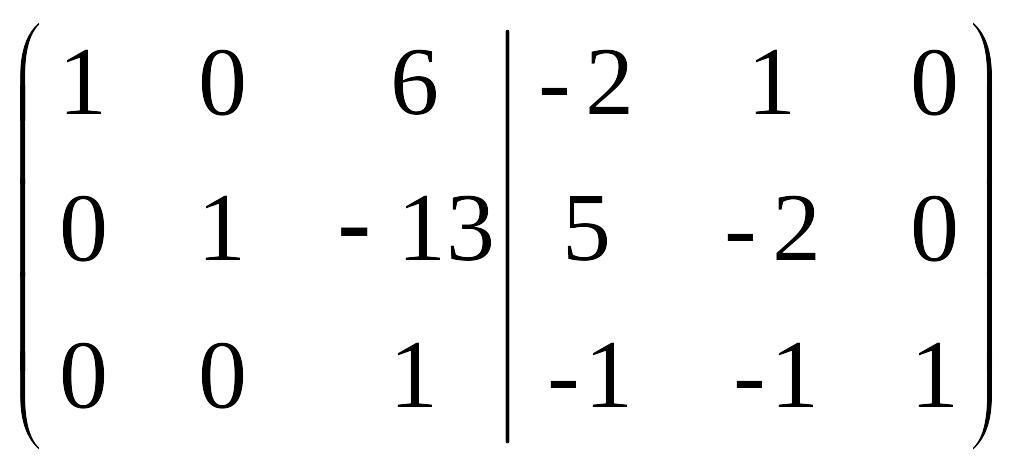
Для реализации обратного хода, домножим третью строку на 13 и прибавим ко второй, а затем домножим третью строку на 6 и вычтем из первой. Тогда

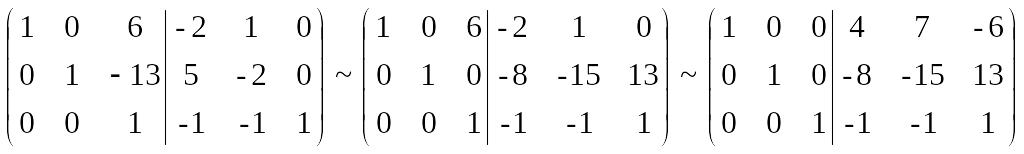
Таким образом, матрица, расположенная после вертикальной черты, является обратной к исходной матрице , т.е.

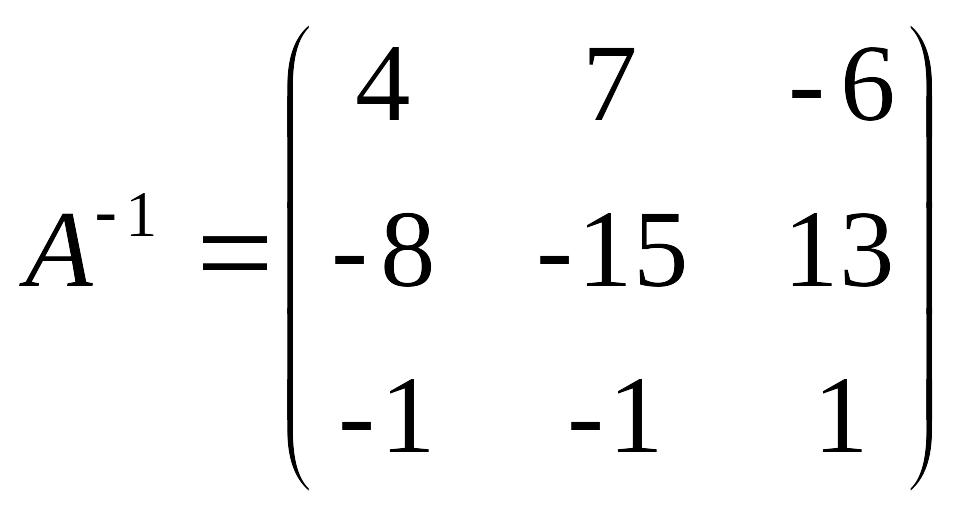
Пример 6. Для четырехотраслевой экономической системы задана матрица коэффициентов прямых материальных затрат. Найти матрицу коэффициентов полных материальных затрат.

Поскольку искомая матрица (см. также пункт 2.4 данного параграфа) является матрицей четвертого порядка, ее вычисление стандартным алгоритмом, описанным в § 1.2, существенно затруднено.

Воспользуемся приведенным в примере 5 методом Гаусса.

Если в нашем примере

,

то преобразования Гаусса необходимо применять к матрице

.

На нулевом шаге для удобства вычислений физически домножим каждую строку на (- 10). Затем из третьей строки вычтем вторую поменяем местами первую строку и новую третью.

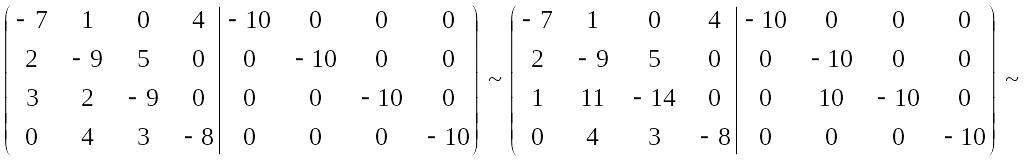
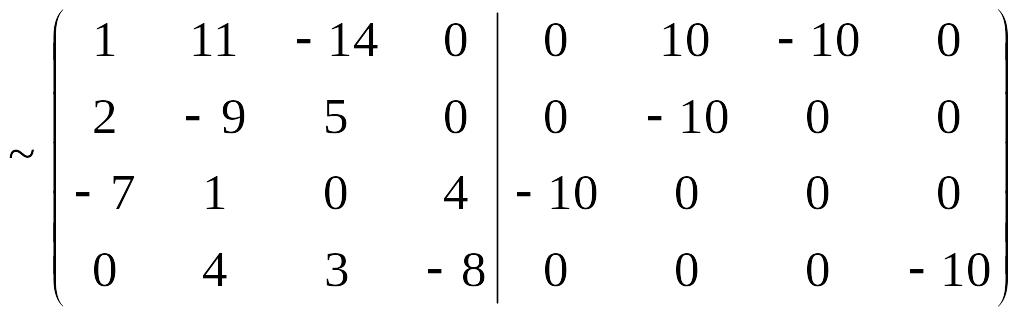
Выполним прямой ход Гаусса. После всех преобразований получим:

.

Разделив последнюю строку на (- 2812) и выполнив обратный ход метода Гаусса, округляя вычисления до 3 знаков после запятой, получаем следующее:

,

т.е. искомая матрица коэффициентов полных материальных затрат равна

.

Очевидно, что данный способ также не очень удобен, особенно обратный ход. В этой ситуации гораздо более простые вычисления дает лемма Ахо.