
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Дискретная математика
Методические указания к выполнению лабораторных работ
ПЕНЗА 2006
УДК 517.5
Приведена методика и даны указания для выполнения лабораторных работ по изучению методов дискретной математики.
Методические указания подготовлены на кафедре «Высшая и прикладная математика» и предназначены для студентов специальности «Прикладная математика», изучающих курс «Дискретная математика».
Составитель - Захарова Ю.Ф.
Рецензент – Гуляев А.В.
Введение
Интерес к дискретной математике объясняется в постоянно растущей в последние десятилетия потребностью в ней в связи с развитием широких областей ее применения – в электронике, информатике, многочисленных вопросах оптимизации. Сейчас повсеместно курсы дискретной математики входят в программы обучения математиков и инженеров. За последние годы появились разнообразные учебники по этой дисциплине, по содержанию разительно не похожие друг на друга.
Целью методических указаний является помощь в изучении дискретной математики, приобретение навыков работы с логическими элементами, а также формирование знаний и умений, которые образуют теоретический фундамент, необходимый для корректной постановки и решения проблем в области информатики, для осознания целей и ограничений при создании вычислительных структур, алгоритмов и программ обработки информации.
Лабораторные работы в представленных методических указаниях охватывают такие разделы дискретной математики, как теория множеств, теория булевых функций, а также кодирование и сжатие графической и текстовой информации и криптографию. В частности, рассматриваются такие важные алгоритмы, как три алгоритма типа слияния из теории множеств, быстрый алгоритм построения совершенной ДНФ, алгоритм Хаффмана сжатия текстовой информации, волновой и ДКП алгоритмы сжатия графической информации и ряд достаточно важных вспомогательных задач, касающихся теории криптографии.
Требования к оформлению отчета о выполнении лабораторной работы
В отчет о выполнении лабораторной работы необходимо включить следующие пункты:
Тема лабораторной работы;
Постановка задачи и вариант задания;
Математическое описание метода решения поставленной задачи;
Результаты выполнения задания;
Программа, реализующая поставленную задачу, должна быть представлена на отдельной дискете.
Лабораторная работа № 1
Алгоритм слияния: включение, объединение и пересечение множеств.
Постановка задачи. Реализовать заданный алгоритм слияния (объединение, включение или пересечение) для заданных неупорядоченных счетных множеств.
Теоретическая часть
Если универсальное множество (универсум) велико или бесконечно, а рассматриваемые подмножества универсума не очень велики, то представление с помощью битовых шкал не является эффективным с точки зрения экономии памяти. В этом случае множества обычно представляются списками элементов. Элемент списка при этом представляется записью с двумя полями: информационным и указателем на следующий элемент. Весь список представляется указателем на следующий элемент.
При таком представлении трудоемкость
операции
![]() составит
составит
![]() ,
а трудоемкость операций
,
а трудоемкость операций
![]() ,
,
![]() и
и
![]() составит
составит
![]() ,
где
,
где
![]() и
и
![]() - мощности участвующих в операции
множеств.
- мощности участвующих в операции
множеств.
Если элементы списка упорядочить ,
например, по возрастанию значения поля
![]() ,
то трудоемкость всех операций составит
.
Эффективная реализация операций над
множествами, представленными в виде
упорядоченных списков, основана на
весьма общем алгоритме, известном как
алгоритм типа слияния.
Алгоритм типа слияния параллельно
просматривает два множества, представленных
упорядоченными списками, причем на
каждом шаге продвижение происходит в
том множестве, в котором текущий элемент
меньше.
,
то трудоемкость всех операций составит
.
Эффективная реализация операций над
множествами, представленными в виде
упорядоченных списков, основана на
весьма общем алгоритме, известном как
алгоритм типа слияния.
Алгоритм типа слияния параллельно
просматривает два множества, представленных
упорядоченными списками, причем на
каждом шаге продвижение происходит в
том множестве, в котором текущий элемент
меньше.
Включение множеств.
Входные параметры: проверяемые предварительно упорядоченные конечные множества А мощности и В мощности .
Выходные параметры:
![]() ,
если
,
если
![]() и
и
![]() ,
если
,
если
![]() .
.
Указатели в списках А и В расположены на первых элементах списков (
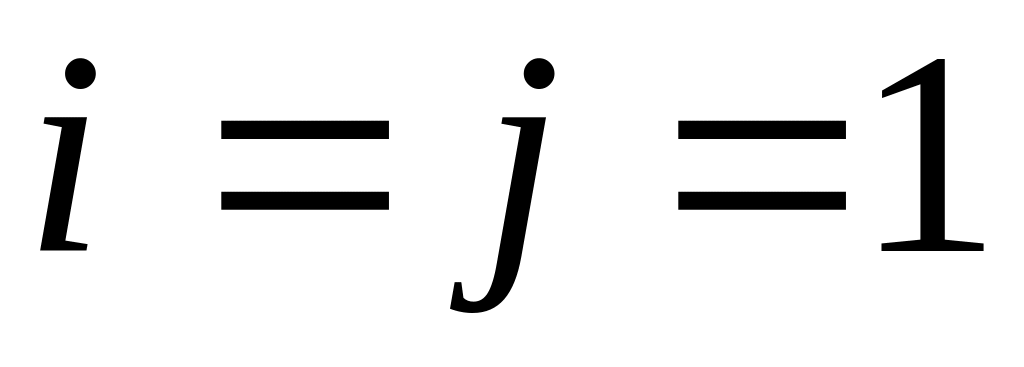 ).
Пока список А не пуст и список В не пуст
(
).
Пока список А не пуст и список В не пуст
(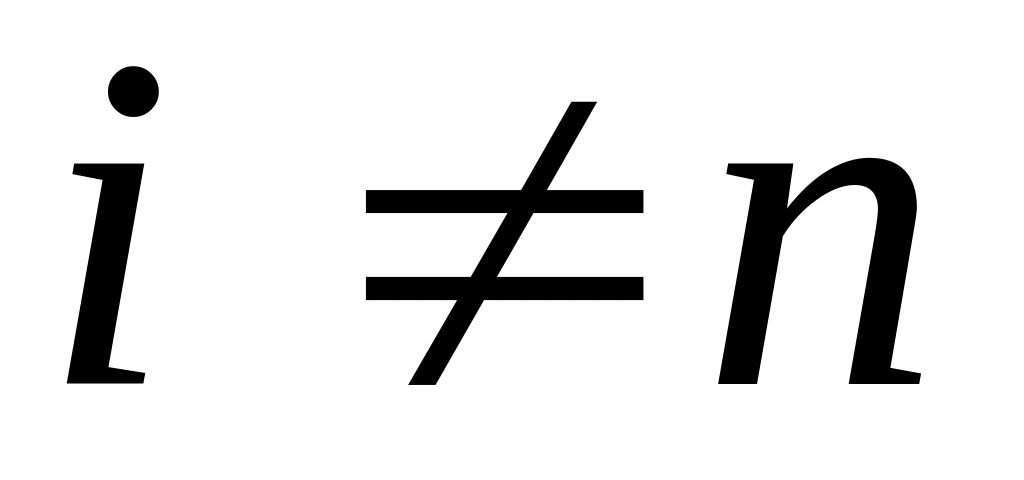 и
и
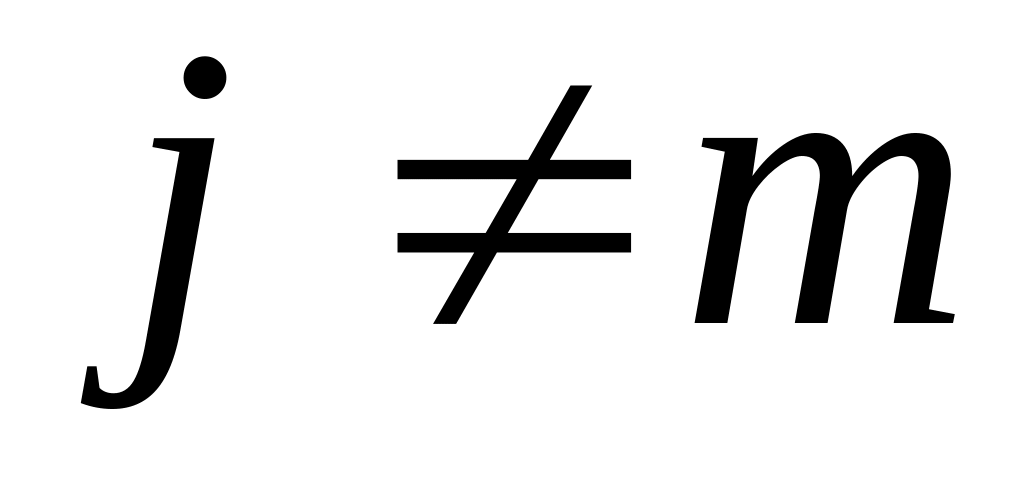 )
выполнять цикл: while
)
выполнять цикл: whileЕсли Аi < Bj, то
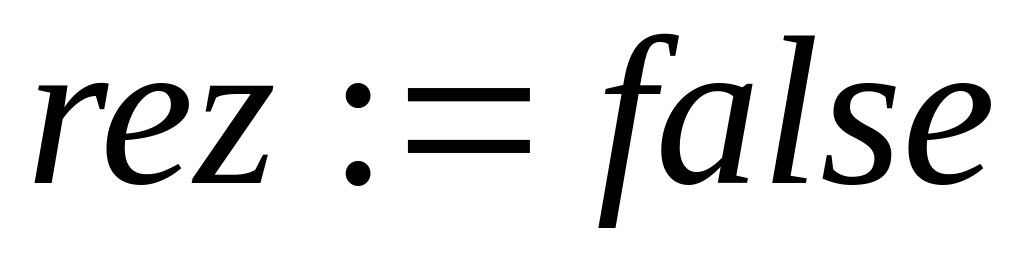 ,
конец цикла;
,
конец цикла;Если Аi > Bj, то
 ,
перейти к 2;
,
перейти к 2;Если Аi = Bj, то ,
 ,
,
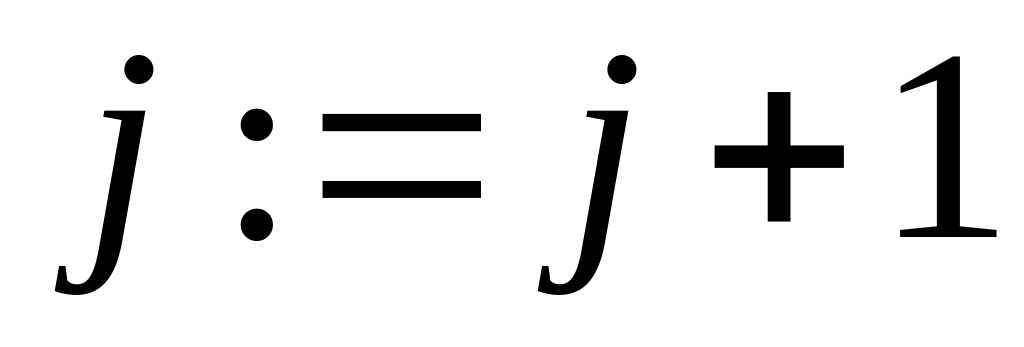 ,
перейти к 2;
,
перейти к 2;End while.
Если , но
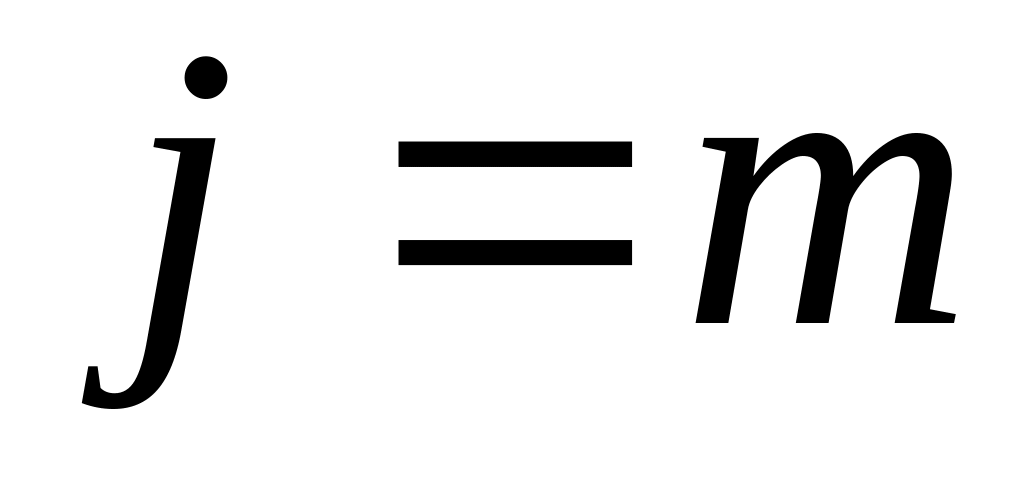 ,
то
.
,
то
.
Объединение множеств.
Входные параметры: проверяемые предварительно упорядоченные конечные множества А мощности и В мощности .
Выходные параметры: конечное
упорядоченное множество С каждый элемент
которого удовлетворяет условию:
![]() .
.
Указатели в списках А и В расположены на первых элементах списков ( ). Список С пуст (
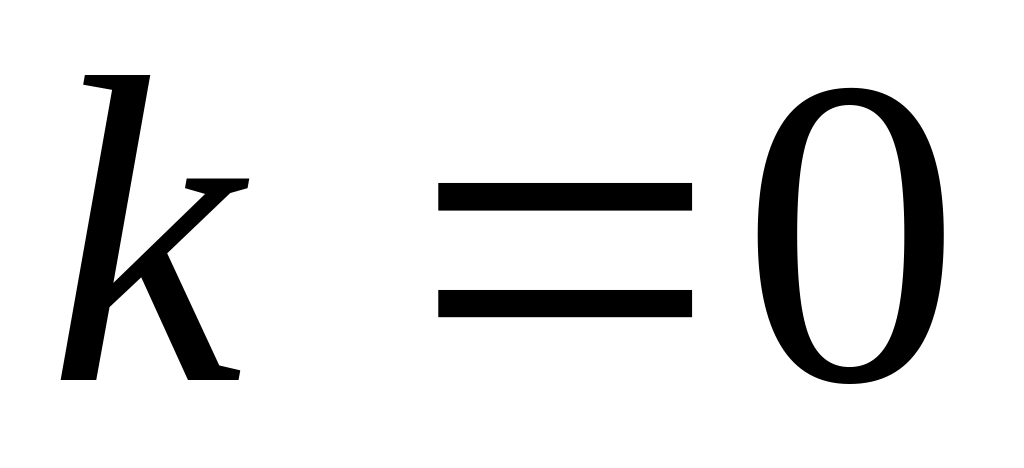 ).
Пока список А не пуст и список В не пуст
(
и
)
выполнять цикл: while
).
Пока список А не пуст и список В не пуст
(
и
)
выполнять цикл: whileЕсли Аi < Bj, то
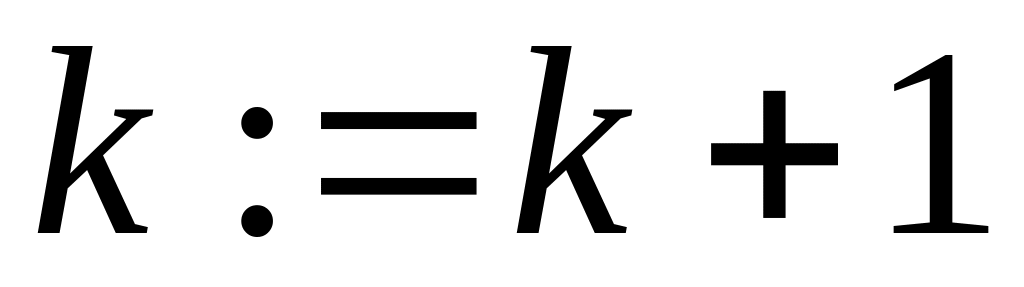 ,
,
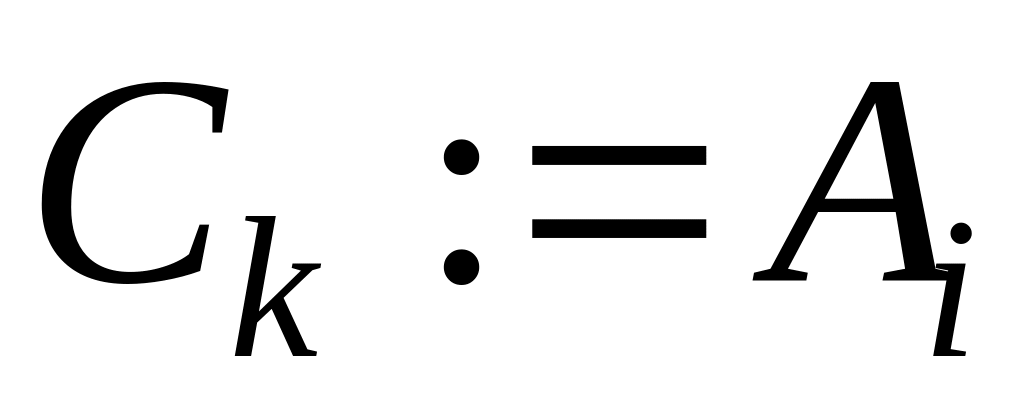 ,
;
,
;Если Аi > Bj, то ,
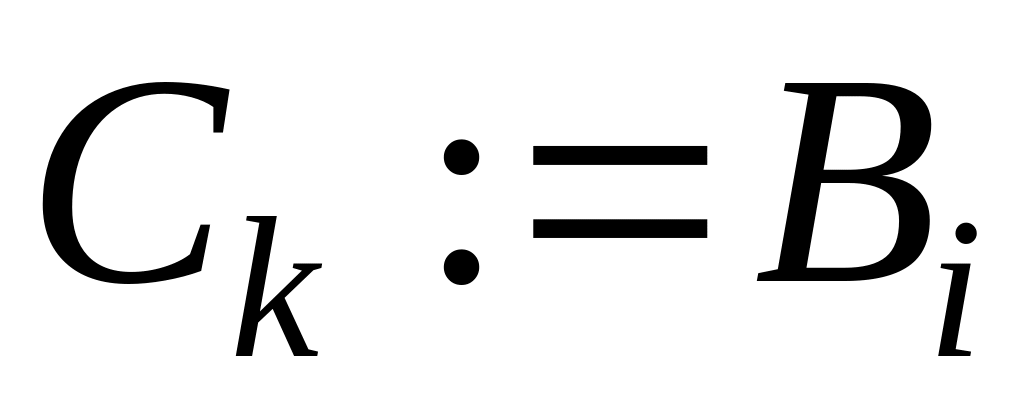 ,
,
перейти к 2;
,
,
перейти к 2;Если Аi = Bj, то , , , , перейти к 2;
End while.
Если , но , то
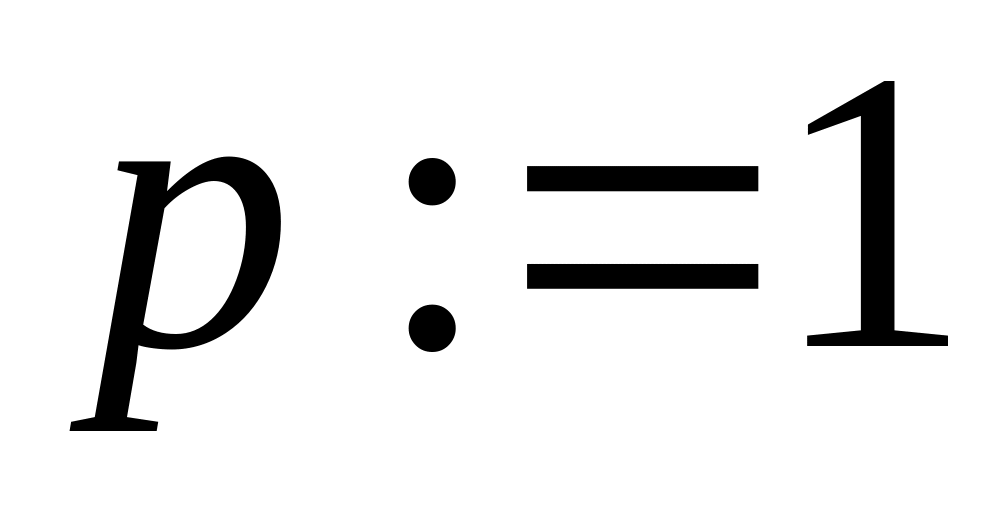 и пока
выполнять цикл: while
и пока
выполнять цикл: while,
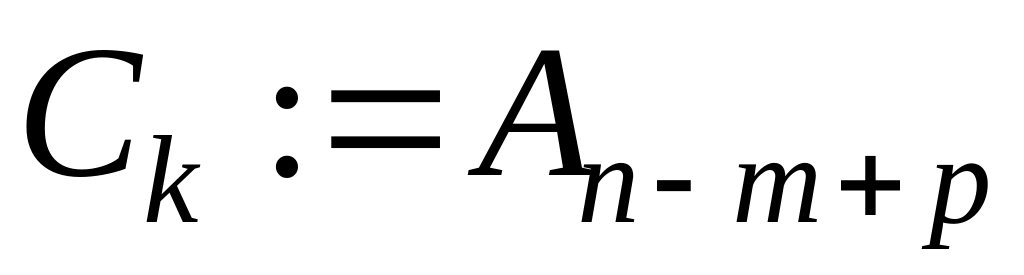 ,
,
 ;
;End while.
Если , но
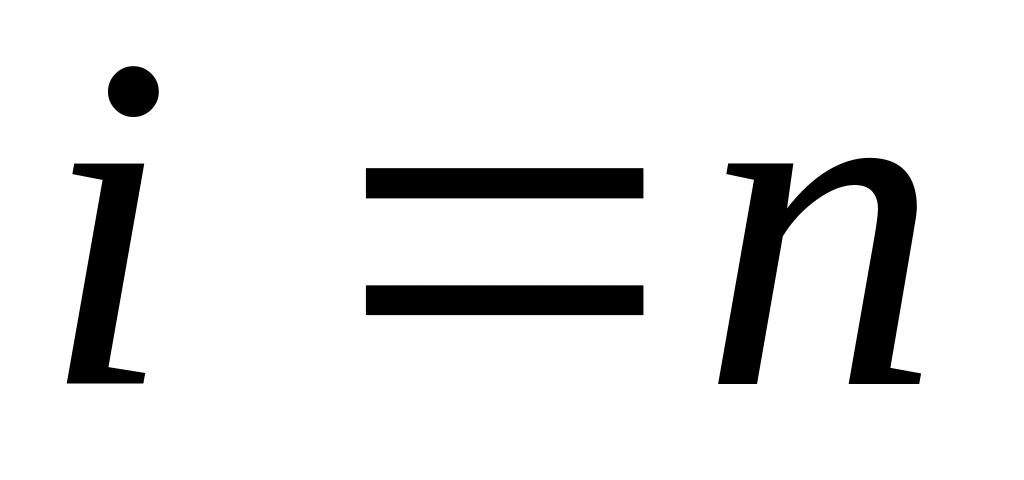 ,
то
и пока
выполнять цикл: while
,
то
и пока
выполнять цикл: while,
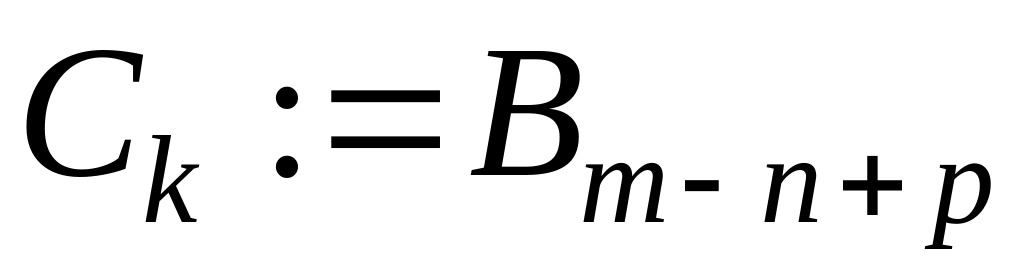 ,
;
,
;End while.
Пересечение множеств.
Входные параметры: проверяемые предварительно упорядоченные конечные множества А мощности и В мощности .
Выходные параметры: конечное
упорядоченное множество С каждый элемент
которого удовлетворяет условию:
![]() .
.
Указатели в списках А и В расположены на первых элементах списков ( ). Список С пуст ( ). Пока список А не пуст и список В не пуст ( и ) выполнять цикл: while
Если Аi < Bj, то ;
Если Аi > Bj, то , перейти к 2;
Если Аi = Bj, то , , , , перейти к 2;
End while.
Указания к выполнению лабораторной работы
Упорядочить заданные вариантом множества. Для упорядочения можно использовать метод «воздушного пузырька», метод топологической сортировки или любой другой известный алгоритм по выбору студента.
Реализовать заданный вариантом алгоритм слияния (включение, объединение или пересечение). Замечание: множества должны быть заданы списками, а не массивами.
Объяснить реализованный алгоритм.
Варианты заданий
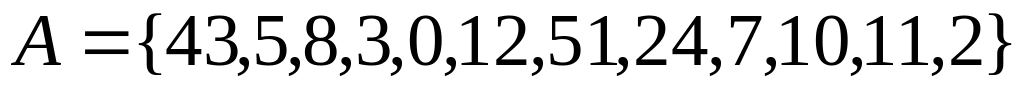 ,
,
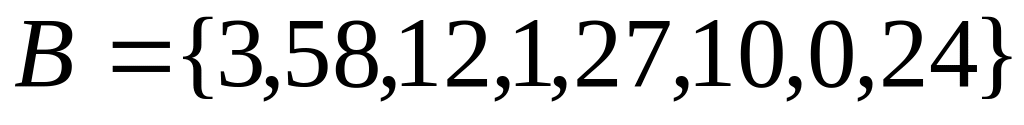 ,
,
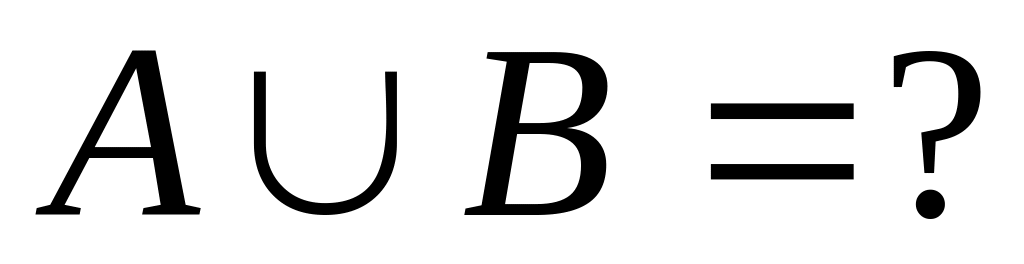
, ,
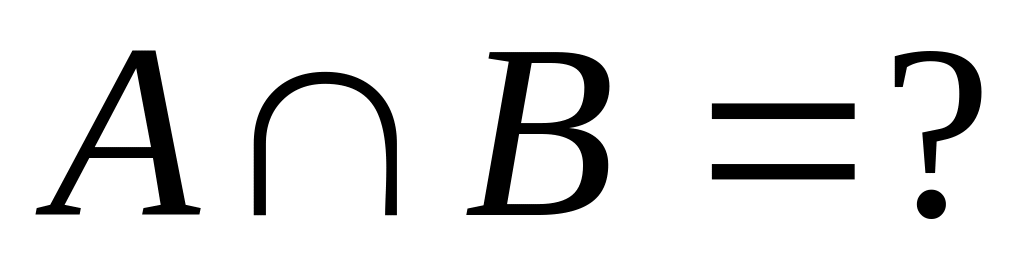
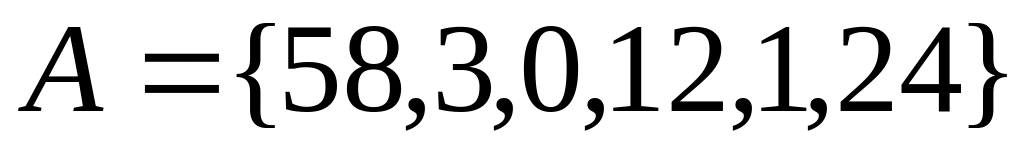 ,
,
,
,
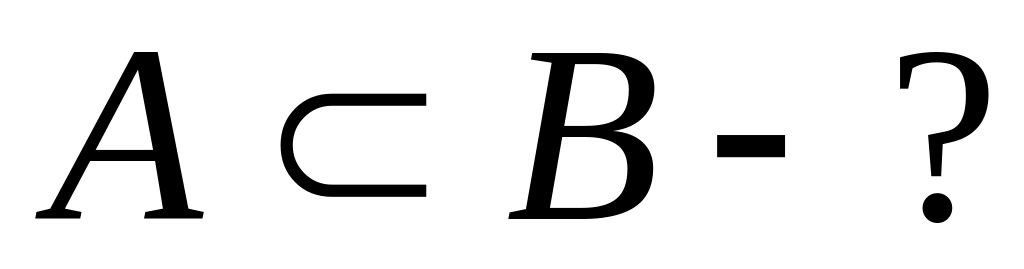
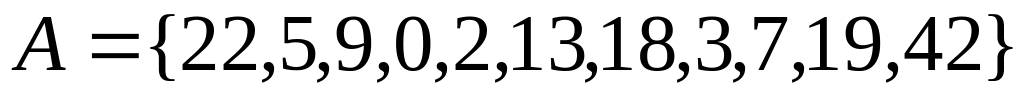 ,
,
 ,
,
, ,
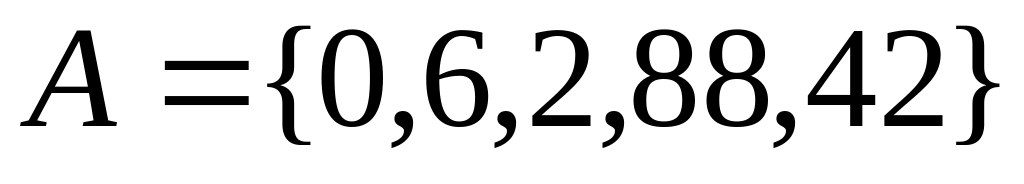 ,
,
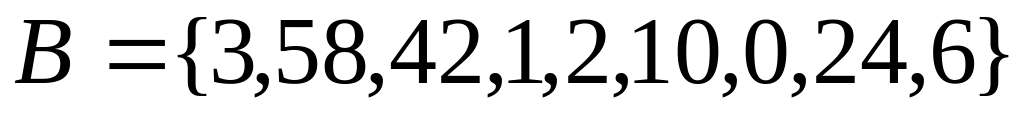 ,
,
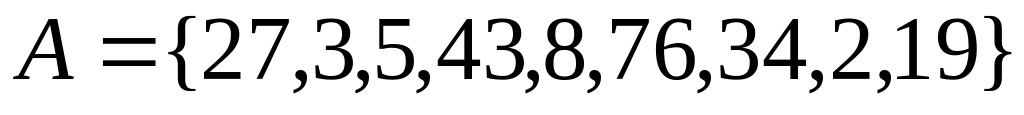 ,
,
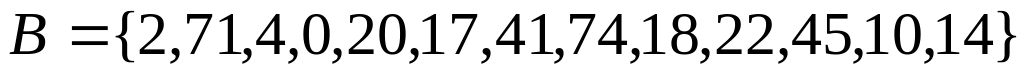 ,
,
, ,
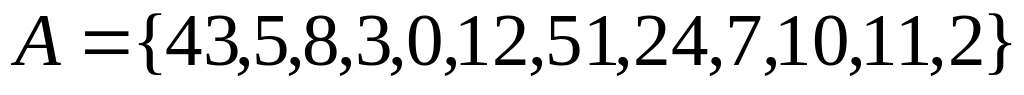 ,
,
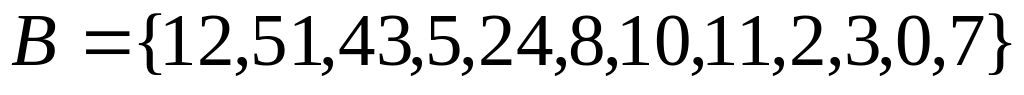 ,
,
 ,
,
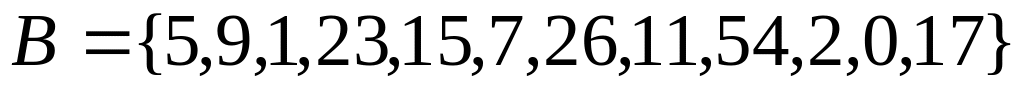 ,
,
, ,
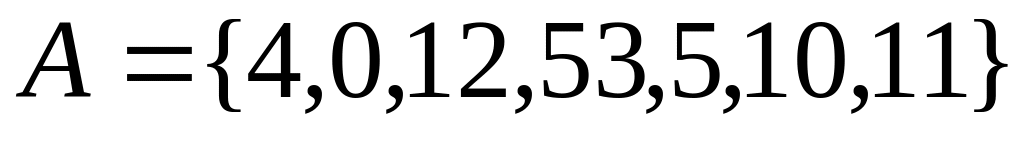 ,
,
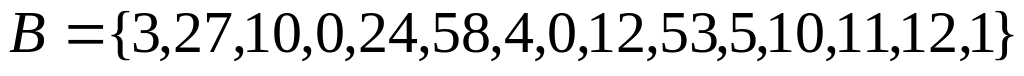 ,
,
Лабораторная работа № 2
Реализация булевых функций формулами.
Постановка задачи. Реализовать формулы над множеством булевых функций, не используя стандартные процедуры, функции и модули, предназначенные для работы с булевыми функциями.
