
- •6.1. Общая теория и примеры. 67 § 1. Матрицы. Основные понятия и действия с ними.
- •1.1. Основные понятия. Вычисление определителя.
- •1.2. Действия с матрицами.
- •1.3. Решение систем линейных алгебраических уравнений.
- •1.4. Примеры для самопроверки. § 2. Метод Гаусса. Лемма Ахо.
- •2.1. Общая теория и примеры.
- •2.2. Лемма Ахо.
- •2.3. Если есть компьютер.
- •§ 3. Экономические задачи, содержащие матрицы и системы.
- •§ 4. Задачи на вектора, прямые и плоскости.
- •4.1. Общая теория и алгоритмы.
- •§ 5. Экономические задачи, содержащие вектора и прямые
- •§ 6. Пределы и производные
- •6.1. Общая теория и примеры.
Содержание:
§ 1. Матрицы. Основные понятия и действия с ними. 2
1.1. Основные понятия. Вычисление определителя. 2
1.2. Действия с матрицами. 9
1.3. Решение систем линейных алгебраических уравнений. 15
1.4. Примеры для самопроверки. 20
§ 2. Метод Гаусса. Лемма Ахо. 21
2.1. Общая теория и примеры. 21
2.2. Лемма Ахо. 32
2.3. Если есть компьютер. 33
§ 3. Экономические задачи, содержащие матрицы и системы. 41
§ 4. Задачи на вектора, прямые и плоскости. 52
4.1. Общая теория и алгоритмы. 52
§ 5. Экономические задачи, содержащие вектора и прямые 59
§ 6. Пределы и производные 67
6.1. Общая теория и примеры. 67 § 1. Матрицы. Основные понятия и действия с ними.
1.1. Основные понятия. Вычисление определителя.
Матрица – прямоугольная таблица
чисел, заключенная, чаще всего1,
в круглые скобки, содержащая
![]() строк и
строк и
![]() столбцов и обозначаемая, как правило,
заглавными буквами латинского алфавита,
например
столбцов и обозначаемая, как правило,
заглавными буквами латинского алфавита,
например
![]() .
При этом сами числа называются элементами
матрицы и обозначаются
.
При этом сами числа называются элементами
матрицы и обозначаются
![]() ,
где
,
где
![]() - номер строки, в которой расположен
элемент, а
- номер строки, в которой расположен
элемент, а
![]() - номер столбца. Сочетание чисел
- номер столбца. Сочетание чисел
![]() называется размерностью матрицы.
называется размерностью матрицы.
Например,
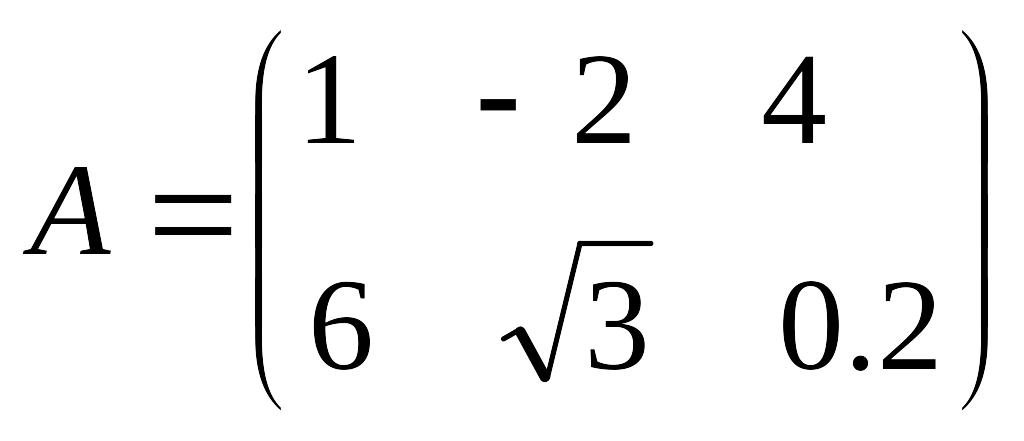
называется матрицей
![]() и ее элемент
и ее элемент
![]() ,
а элемент
,
а элемент
![]() и т.д.
и т.д.
Если число строк и число столбцов матрицы совпадают, то матрица называется квадратной.
Все элементы квадратной матрицы2, расположенные вдоль линии, соединяющей левый верхний угол с правым нижним, называются главной диагональю матрицы.
Все элементы квадратной матрицы, расположенные вдоль линии, соединяющей правый верхний угол с левым нижним, называются побочной диагональю матрицы.
Например для матрицы
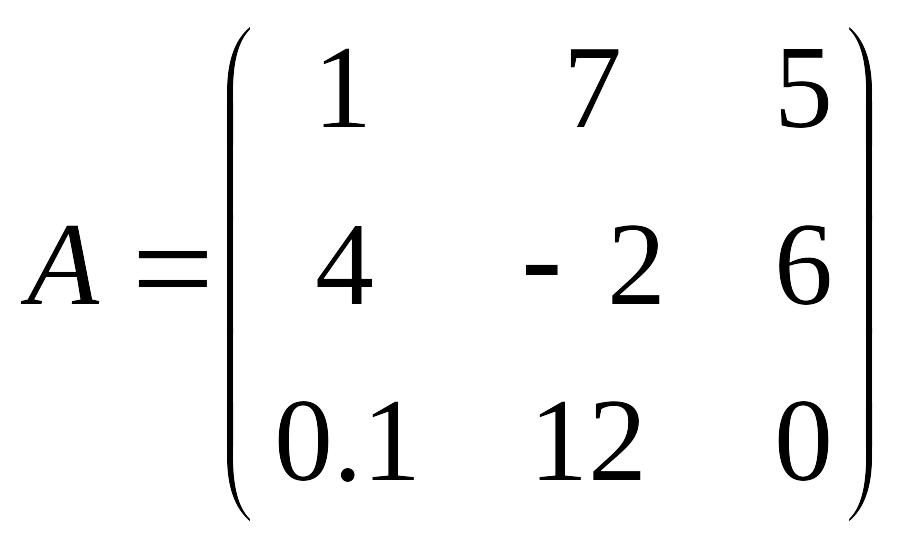
элементы 1, -2 и 0 являются главной диагональю, а элементы 5, -2 и 0.1 – побочной.
Если выше или ниже главной или побочной диагоналей все элементы матрицы равны 0, то матрица называется треугольной.
Например, матрицы


 и
и
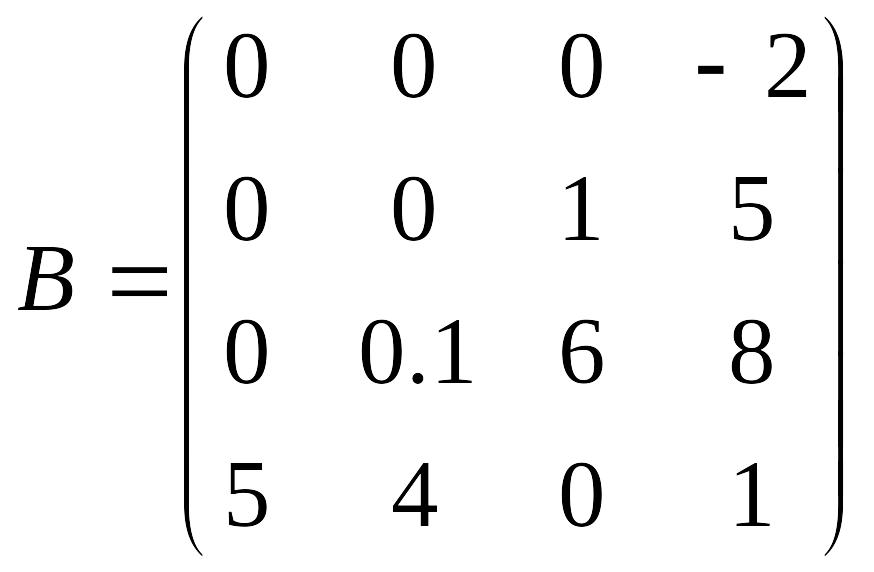
является треугольными. При этом матрица
называется верхнетреугольной (ненулевые
элементы расположены выше диагонали),
а матрица
![]() - нижнетреугольной (ненулевые элементы
расположены ниже диагонали).
- нижнетреугольной (ненулевые элементы
расположены ниже диагонали).
Матрица называется нулевой, если все ее элементы равны 0.
Матрица называется единичной, если на главной ее диагонали все элементы равны 1, а все ее остальные элементы равны 0.
Примером единичной матрицы размером
![]() может быть такая:
может быть такая:
![]()
Определителем квадратной (и
только квадратной) матрицы
называется число, обозначаемое как
![]() или
или
![]() ,
вычисляемое по одному из следующих
правил – свойств определителя:
,
вычисляемое по одному из следующих
правил – свойств определителя:
1) Определитель матрицы вычисляется по правилу «креста»:
если
 ,
то
,
то 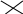
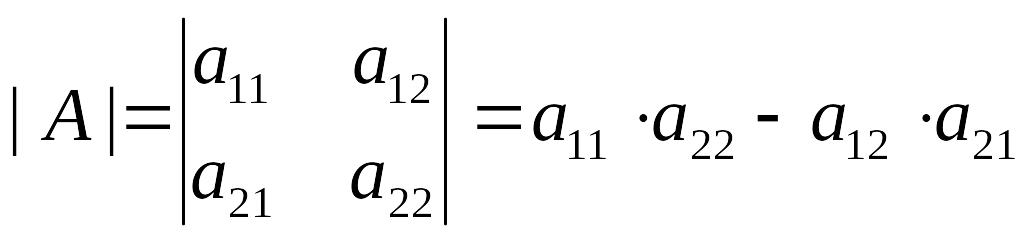
2) Определитель матрицы
![]() вычисляется по правилу «треугольника»:
вычисляется по правилу «треугольника»:
если
 ,
то
,
то


Схематично, чтобы представить себе, почему правило названо правилом «треугольника», это можно изобразить так:
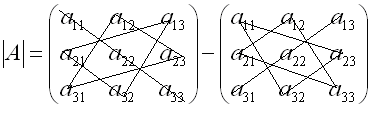
3) Определитель треугольной матрицы всегда равен произведению диагональных элементов, если диагональ главная и произведению диагональных элементов, взятому с противоположным знаком, если диагональ побочная.
4) Если все элементы хотя бы одной строки
или одного столбца матрицы равны нулю,
то
![]() .
.
5) Если хотя бы два столбца или две строки матрицы равны между собой, то .
6) Если вся строка или весь столбец
матрицы делятся на одно и то же число
![]() - это число может быть вынесено за знак
определителя.
- это число может быть вынесено за знак
определителя.
7) Если две строки или два столбца матрицы поменять местами, то определитель изменит свой знак на противоположный.
8) Определитель не измениться, если к любой строке (или столбцу) добавить любую другую строку (или столбец), домноженную на любое число.
9) Определитель может быть вычислен как сумма элементов любой строки (или столбца), домноженных на свои алгебраические дополнения.
Алгебраическим дополнением
некоторого элемента
![]() называется определитель матрицы,
оставшийся после вычеркивания где
-й
строки и
-го
столбца, взятый с учетом знака
называется определитель матрицы,
оставшийся после вычеркивания где
-й
строки и
-го
столбца, взятый с учетом знака
![]() .
.
Рассмотрим ряд примеров по каждому из приведенных свойств.
Пример 1. Вычислить определитель:
![]() .
.
В соответствии с первым свойством:
![]()
Пример 2. Вычислить определитель:
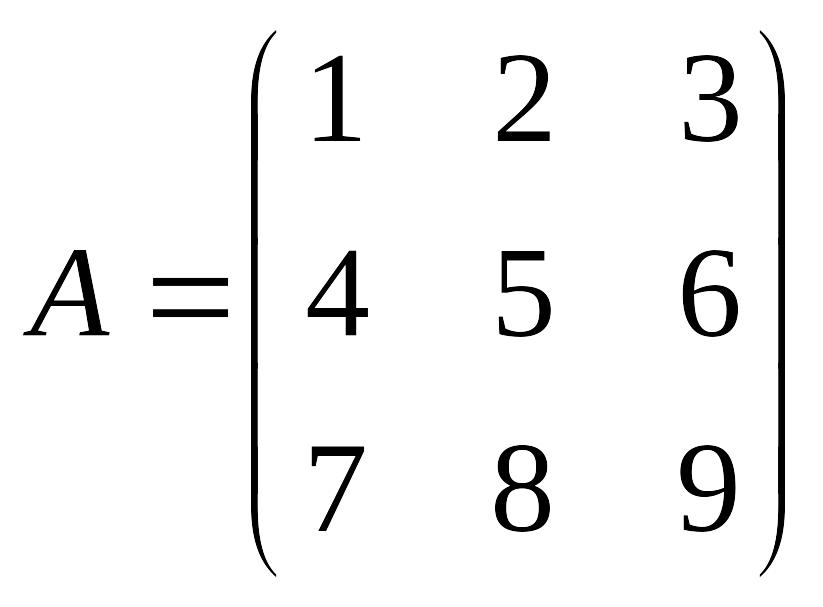 .
.
В соответствии со вторым свойством:

Пример 3. Вычислить определитель:
В соответствии с третьим свойством, данный определитель равен
![]() .
.
Убедимся в том, что это действительно так, с помощью второго свойства:

Пример 4. Вычислить определитель:
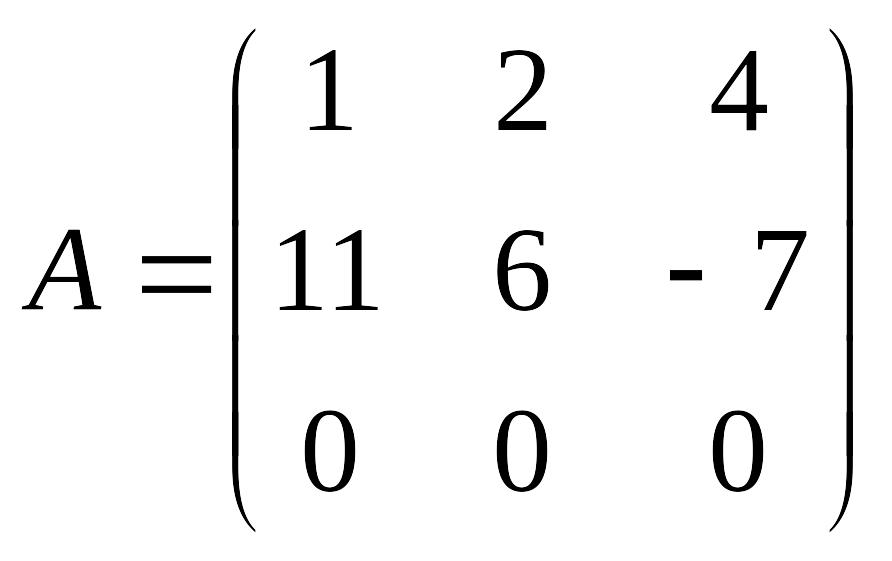
В соответствии с четвертым свойством, данный определитель равен нулю. Убедимся в том, что это действительно так, с помощью второго свойства:

Пример 5. Вычислить определитель:

В соответствии с пятым свойством, данный определитель равен нулю. Убедимся в том, что это действительно так, с помощью второго свойства:
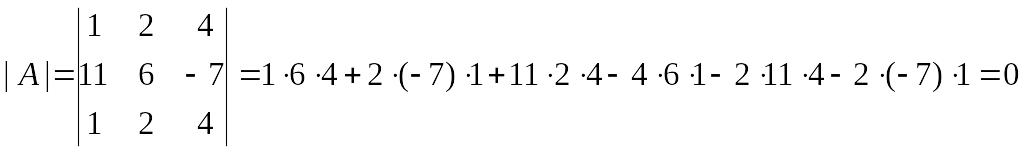
Пример 6. Вычислить определитель:

Для начала вычислим определитель, пользуясь лишь вторым свойством:

Данные вычисления не являются удобными. Заметим, однако, что вся первая строка делится на 60, вся вторая – на 100, а вся третья – на 40. Тогда, в соответствии с шестым свойством,

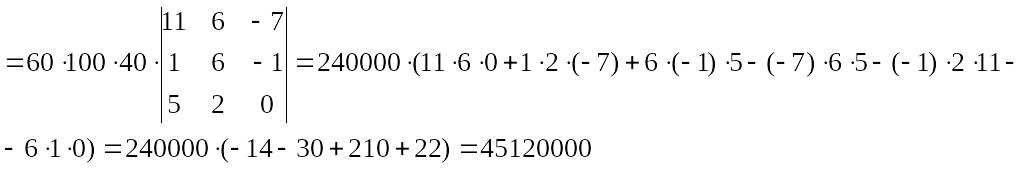
Пример 7. Доказать свойство 7 на примере вычисления определителей матриц
 и
и

Заметим, что две данные матрицы различаются лишь тем, что в них переставлены местами первый и второй столбцы. В соответствии с правилом треугольника (промежуточные вычисления здесь и далее предлагается выполнить самостоятельно по аналогии с рассмотренными ранее примерами)

 ,
,
что и требовалось доказать.
Пример 8. Вычислить определитель:
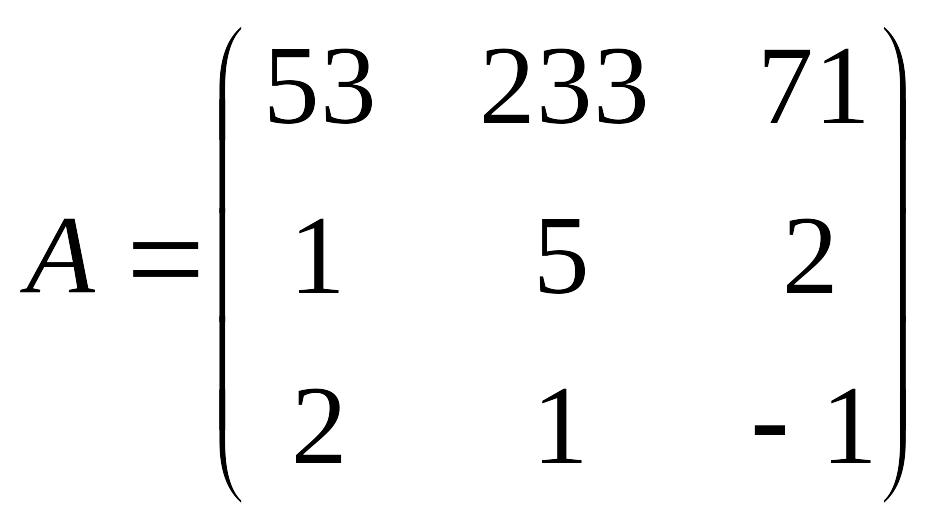
Здесь нет возможности воспользоваться рассмотренным ранее свойством 6 – большие числа первой строки не имеют ни одного общего делителя. Применим свойство 8. Домножим вторую строку на 46. При этом чрезвычайно важным является следующий факт: физически вторая строка не изменяется, результат умножения мы держим «в уме» или же подписываем «тонким карандашом, мелким шрифтом» рядом с реальными числами. Т.е.
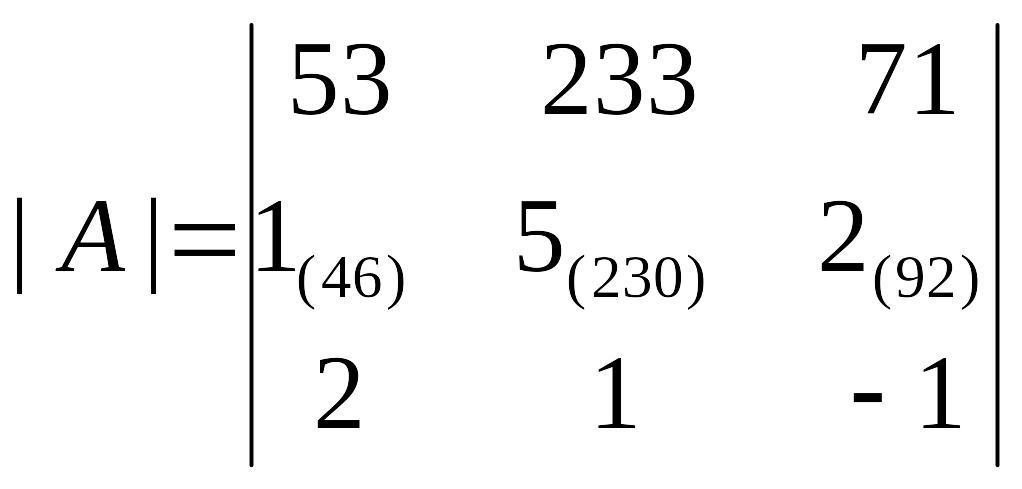
После чего из первой строки вычтем почленно результат умножения (всю подписанную строку, которую теперь можно «стереть»). Применяя затем правило треугольника, получаем
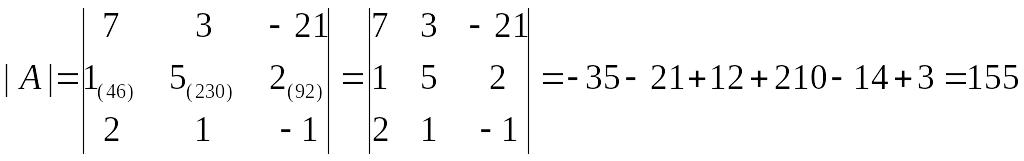
Убедимся в том, что это действительно так – вычислим определитель исходной, непреобразованной матрицы с помощью правила треугольника:

Очевидно, что числа преобразованной матрицы более удобны для счета, а результат при этом не изменяется.
Пример 9. Вычислить определитель:
Воспользуемся результатом, полученным
в примере 8, для иллюстрации последнего
и очень важного свойства. Разложим
определитель данной матрицы, например,
по первой строке. Алгебраическое
дополнение элемента
![]() ,
,
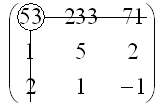
в соответствии с определением, будет вычисляться следующим образом:
![]()
Алгебраическое дополнение элемента
![]() ,
,
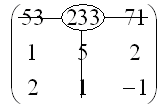
будет вычисляться следующим образом:
![]()
И, наконец, алгебраическое дополнение
элемента
![]() ,
,
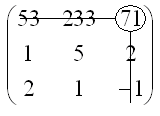
будет вычисляться следующим образом:
![]() .
.
Тогда окончательно
![]()
Аналогично, определитель может быть вычислен путем разложения по любой из оставшихся строк и любому столбцу.
Вычисление определителей матриц выше 3-го порядка также осуществляется на основании 9-го свойства. Достаточно удобным для этих целей является метод Гаусса, описанный в §2.1.
