2.7. Построение логарифмических характеристик сау
Передаточные функции разомкнутых и замкнутых САУ можно привести к виду
(2.143)
где
– передаточные функции элементарных
звеньев.
Тогда частотная передаточная функция
.
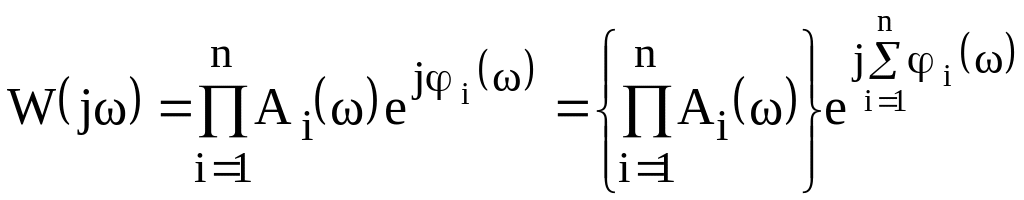(2.144)
Отсюда ФЧХ (ЛФЧХ), АЧХ и ЛАЧХ определяются выражениями
;
(2.145)
;
(2.146)
.
(2.147)
Таким образом, результирующие логарифмические фазо-частотная и амплитудно-частотная характеристики могут быть построены как суммы ЛФЧХ (ЛАЧХ) отдельных звеньев.
Рассмотрим в качестве примера построение асимптотических логарифмических частотных характеристик разомкнутой САУ, передаточная функция которой равна
,
(2.148)
где k = 10; T = 10 c.
Выражение (2.148) свидетельствует о том, что разомкнутая цепь САУ содержит последовательно включенные интегрирующее и апериодическое звенья
.
(2.149)
Рассчитаем
сопрягающую частоту апериодического
звена
.
Согласно выражению (2.36), асимптотическая ЛАХ рассматриваемого интегрирующего звена
.
(2.150)
Она
проходит через точку с координатами
– см. рисунок 2.53.
Рисунок 2.53
В соответствии с формулами (2.35) и (2.36), асимптотическая ЛАХ рассматриваемого апериодического звена
.
(2.151)
Она
проходит через точку с координатами
– см. рисунок 2.53.
График
результирующей ЛАХ разомкнутой САУ
приведен на рисунке 2. 54 (сплошная линия).
Рисунок 2.54
Отметим, что продолжение низкочастотной асимптоты ЛАХ (пунктирная линия на рис. 2.54) по-прежнему (как и на рис. 2.53) проходит через точку с координатами .
В соответствии с выражениями (2.43) и (2.30), ЛФЧХ рассматриваемых интегрирующего и апериодического звеньев
;
(2.152)
.
(2.153)
Графики
(2.152), (2.153), а также результирующей ЛФХ
разомкнутой САУ (
)
приведены на рисунке 2.55.
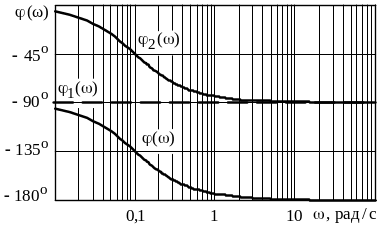
Рисунок 2.55
Из данного примера следует, что для получения результирующей ЛАХ не обязательно строить ЛАХ отдельных звеньев. Рассмотрим следующий алгоритм построения.
1. Перепишем формулу (2.143) в виде
,
(2.154)
где
;
– полиномы
вида
,
;
– полиномы
вида
,
.
Отметим,
что ЛАХ и ЛФХ дифференцирующего звена
второго порядка с передаточной функцией
отличаются от соответствующих
характеристик колебательного звена
только знаком.
2.
Определяем сопрягающие частоты
,
и отмечаем их на оси абсцисс.
3.
Строим низкочастотную асимптоту ЛАХ с
наклоном (
)
дБ/дек. Ордината этой асимптоты или ее
продолжение на частоте
должна быть равна
.
Заканчивается низкочастотная асимптота
на первой сопрягающей частоте.
4. После первой и всех последующих сопрягающих частот наклон асимптотической ЛАХ изменяется. На сопрягающих частотах, созданных полиномами числителя (2.154), изменение наклона положительное, а созданных полиномами знаменателя – отрицательное. Полином первой степени изменяет наклон на 20 дБ/дек, полином второй степени – на 40дБ/дек.
Рассмотрим в качестве примера построение ЛАХ разомкнутой САУ с передаточной функцией
,
(2.155)
где
k
= 100;
с;
с;
с;
.
Тогда
сопрягающие частоты
;
;
.
Наносим отметки сопрягающих частот на
ось абсцисс
(рис. 2.56).
Перепишем для удобства формулу (2.155) в порядке следования сопрягающих частот
.
(2.156)
Строим
низкочастотную часть ЛАЧХ (рис. 2. 56).
Поскольку в функции (2.156) величина
,
то наклон ЛАХ в области низких частот
равен
(– 20 дБ/дек). Продолжение данной
асимптоты проходит через точку с
координатами
.
Заканчивается низкочастотная асимптота
на первой сопрягающей частоте
.
Рисунок 2.56
Поскольку
первая сопрягающая частота создается
полиномом знаменателя первого порядка
,
то он изменяет наклон второй асимптоты
на
(– 20 дБ/дек) – рисунок 2.56.
Заканчивается вторая асимптота на
второй сопрягающей частоте
.
Вторая
сопрягающая частота создается полиномом
числителя первого порядка
.
В этом случае происходит изменение
наклона третьей асимптоты на (+ 20 дБ/дек)
– рисунок 2.56. Заканчивается третья
асимптота на третьей сопрягающей частоте
.
Третья
сопрягающая частота создается полиномом
знаменателя второго порядка
,
что приводит к изменению наклона
четвертой асимптоты на (– 40 дБ/дек).