
- •Визначники
- •1. Визначники другого та третього порядків
- •2. Властивості визначників
- •3. Розклад визначника за елементами рядка або стовпця
- •4. Поняття про визначники вищих порядків
- •Матриці
- •Системи лінійних рівнянь
- •Функція багатьох змінних, її границя та неперервність
- •Лекція №2. Частинні похідні функції багатьох змінних. Диференційовність функції багатьох змінних.
- •Диференціал функції багатьох змінних
- •Локальні екстремуми функції багатьох змінних
- •Умовний екстремум функції багатьох змінних
- •Диференціальне числення функції багатьох змінних
- •Визначений інтеграл
- •Диференціальні рівняння першого порядку
Визначений інтеграл
Задача про площу криволінійної трапеції. Означення та умови існування визначеного інтеграла
Властивості визначеного інтеграла
Формула Ньютона-Лейбніца. Методи обчислення визначених інтегралів
Застосування визначеного інтеграла
1. Задача про площу криволінійної трапеції. Означення та умови існування визначеного інтеграла
Нехай на відрізку
![]() задано функцію
задано функцію
![]() .
Фігура, обмежена графіком даної функції
і відрізками прямих
.
Фігура, обмежена графіком даної функції
і відрізками прямих
![]() ,
називається криволінійною
трапецією.
Обчислимо площу цієї трапеції.
,
називається криволінійною
трапецією.
Обчислимо площу цієї трапеції.
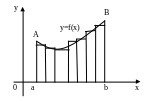
Розіб’ємо відрізок
![]() на
довільних частин точками:
на
довільних частин точками:
![]() .
.
Сукупність точок
![]() позначимо через Т і назвемо Т–розбиттям
відрізка
.
позначимо через Т і назвемо Т–розбиттям
відрізка
.
На кожному частинному
відрізку
![]() ,
візьмемо довільну точку
,
візьмемо довільну точку
![]() і обчислимо значення
і обчислимо значення
![]() .
Тоді добуток
.
Тоді добуток
![]() ,
де
,
де
![]() - довжина відрізка
- довжина відрізка
![]() дорівнює площі прямокутника з основою
дорівнює площі прямокутника з основою
![]() і висотою
,
а сума цих добутків
і висотою
,
а сума цих добутків
![]() (1) – площа ступінчатої фігури і наближено
дорівнює площі криволінійної трапеції:
(1) – площа ступінчатої фігури і наближено
дорівнює площі криволінійної трапеції:
![]() . (2)
. (2)
Сума (1) називається
інтегральною
сумою функції
![]() ,
яка відповідає
Т-розбиттю відрізка
на частинні відрізки і даному вибору
точок
,
яка відповідає
Т-розбиттю відрізка
на частинні відрізки і даному вибору
точок
![]() .
.
Із зменшенням усіх величин точність формули (2) збільшується, тому природно за площу криволінійної трапеції вважати границю площ ступінчатих фігур за умови, що максимальна довжина частинних відрізків прямує до нуля:
![]() .
.
Якщо існує скінченна
границя інтегральної суми (1) при
![]() ,
яка не залежить ні від Т–розбиття, ні
від вибору точок
,
то ця границя називається визначеним
інтегралом
функції
на відрізку
,
яка не залежить ні від Т–розбиття, ні
від вибору точок
,
то ця границя називається визначеним
інтегралом
функції
на відрізку
![]() і позначається символом
і позначається символом
![]() .
.
Отже, згідно з
означенням: ![]() .
.
Функція
називається інтегрованою
на відрізку
.
Числа
![]() називаються відповідно нижньою
і верхньою
межею інтегрування;
функція
називається підінтегральною
функцією;
називаються відповідно нижньою
і верхньою
межею інтегрування;
функція
називається підінтегральною
функцією;
![]() – підінтегральним
виразом;
– змінною інтегрування;
– проміжком
інтегрування.
– підінтегральним
виразом;
– змінною інтегрування;
– проміжком
інтегрування.
Площа криволінійної
трапеції, обмеженої прямими
![]() і
графіком функції
,
дорівнює визначеному інтегралу від
цієї функції
і
графіком функції
,
дорівнює визначеному інтегралу від
цієї функції
![]() .
У цьому полягає геометричний зміст
визначеного інтеграла: визначений
інтеграл від невід’ємної функції
чисельно дорівнює площі відповідної
криволінійної трапеції.
.
У цьому полягає геометричний зміст
визначеного інтеграла: визначений
інтеграл від невід’ємної функції
чисельно дорівнює площі відповідної
криволінійної трапеції.
Умови інтегрованості функцій:
Теорема 1 (необхідна умова інтегровності)
Якщо функція інтегровна на відрізку , то вона обмежена на цьому відрізку.
Теорема 2 (достатня умова інтегровності)
Якщо функція неперервна на відрізку , то вона інтегровна на цьому відрізку.
Теорема 3
Якщо функція обмежена на відрізку і неперервна в ньому скрізь, крім скінченного числа точок, то вона інтегровна на цьому відрізку.
Теорема 4
Всяка обмежена і монотонна на відрізку функція інтегровна на цьому відрізку.
2. Властивості визначеного інтеграла
Величина визначеного інтеграла не залежить від позначення змінної інтегрування:
![]() .
.
Визначений інтеграл з однаковими межами інтегрування дорівнює нулю:
![]() .
.
Від перестановки меж інтегрування інтеграл змінює знак на протилежний:
![]() .
.
Якщо функція інтегровна на максимальному з відрізків
 ,
то справедлива рівність:
,
то справедлива рівність:
![]() .
.
Сталий множник С можна винести за знак визначеного інтеграла:
![]() .
.
Визначений інтеграл від суми інтегрованих функцій дорівнює сумі визначених інтегралів від цих функцій:
![]() .
.
Якщо всюди на відрізку маємо
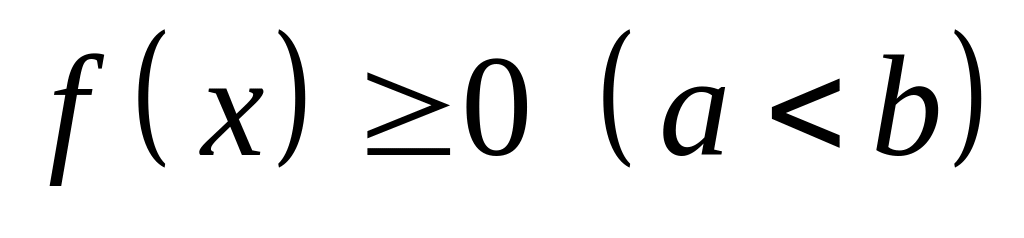 ,
то
,
то
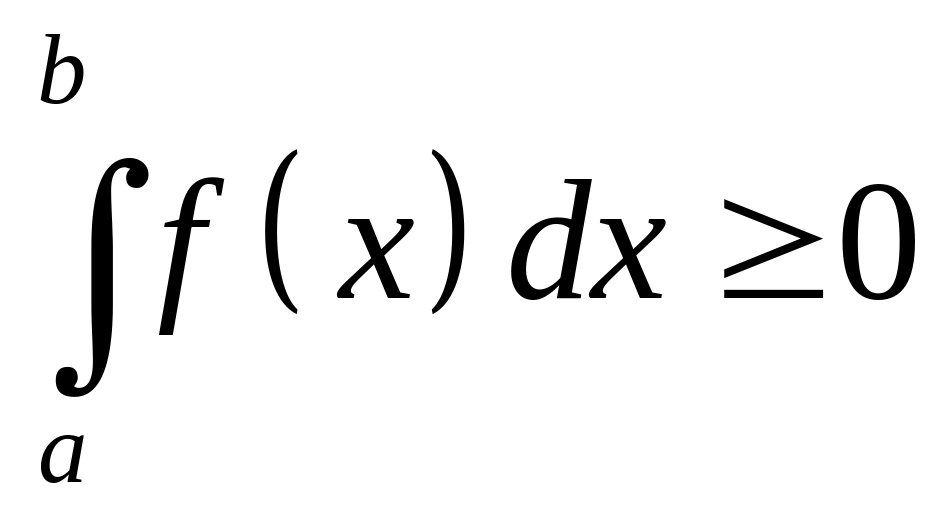 .
.Якщо всюди на відрізку маємо
 ,
то
,
то
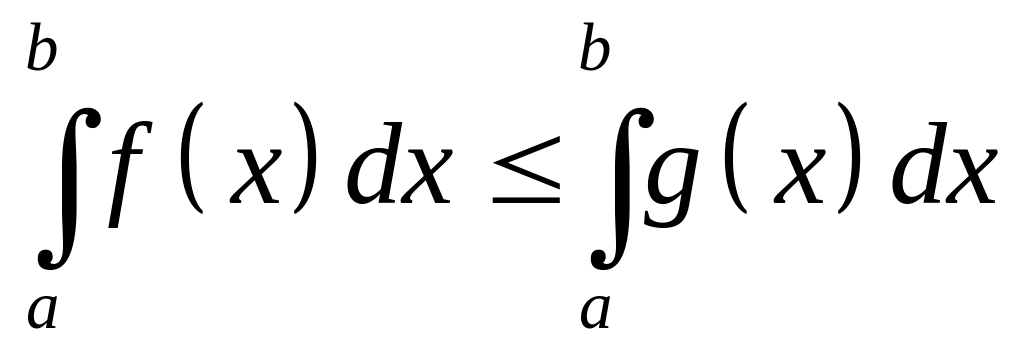 .
.Якщо функція інтегровна на відрізку
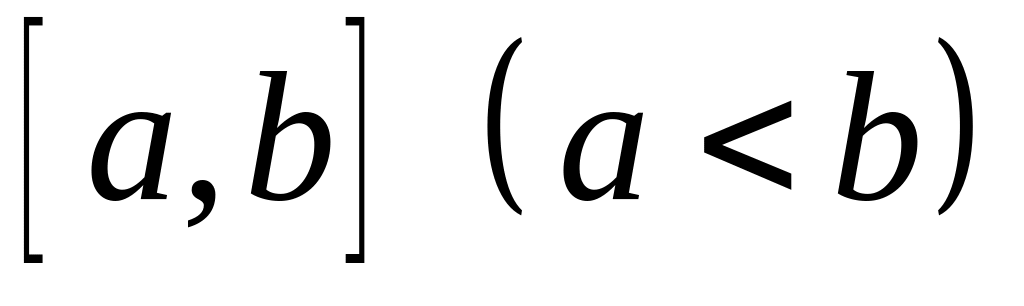 ,
то
,
то
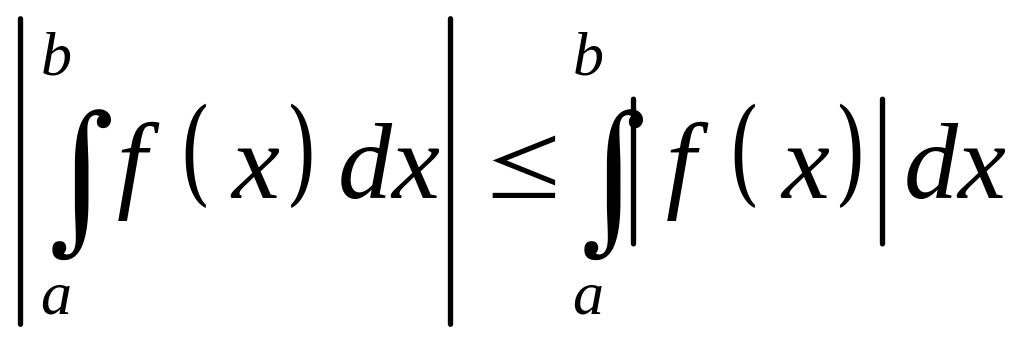 .
.Якщо
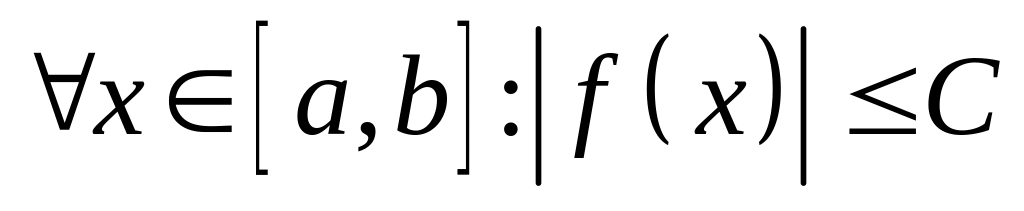 ,
то
,
то 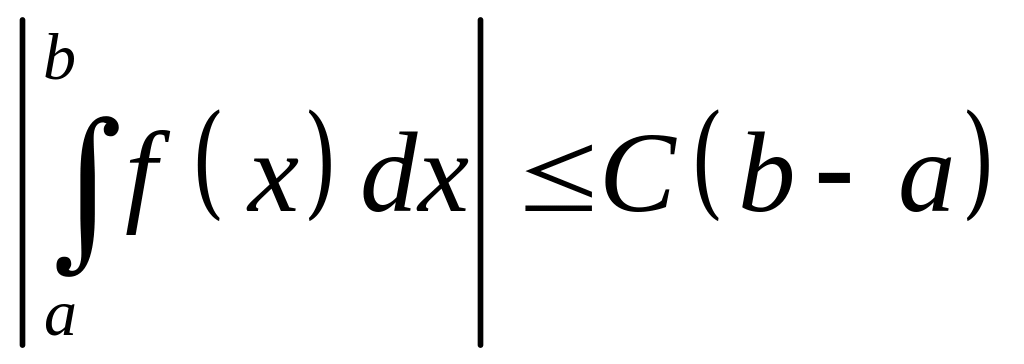 .
.Якщо
 і
- відповідно найбільше і найменше
значення функції
на відрізку
,
то
і
- відповідно найбільше і найменше
значення функції
на відрізку
,
то
![]() .
.
Якщо функція неперервна на відрізку , то на цьому відрізку знайдеться така точка , що
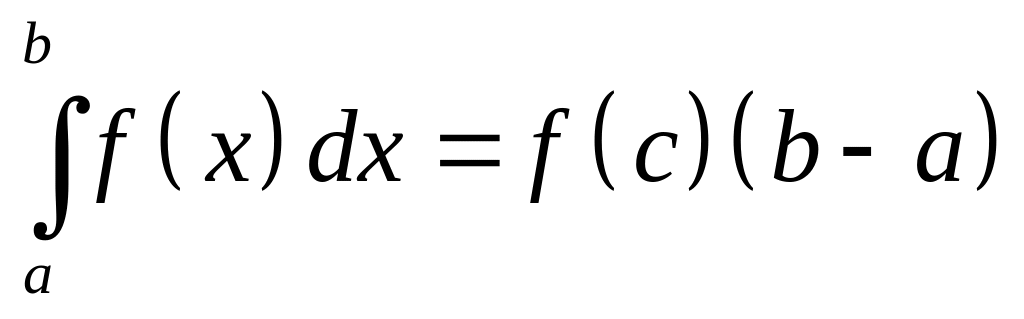 .
.
3. Формула Ньютона-Лейбніца. Методи обчислення визначених інтегралів
Теорема.
Якщо
![]() є якою-небудь первісною від неперервної
функції
є якою-небудь первісною від неперервної
функції
![]() ,
то справедлива формула
,
то справедлива формула
![]() .
.
Ця формула називається формулою Ньютона-Лейбніца.
Методи обчислення визначених інтегралів:
Метод заміни змінної (метод підстановки)
Теорема 1
Нехай виконуються умови:
функція неперервна на відрізку ;
функція
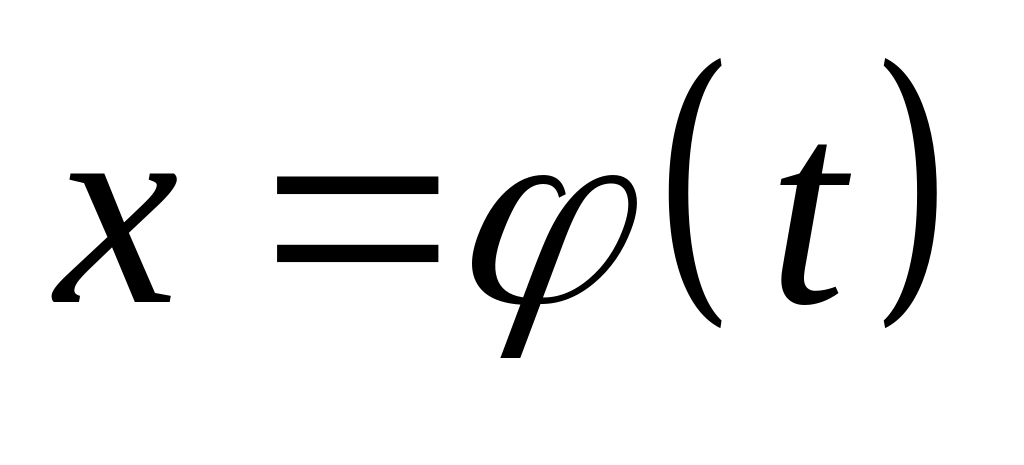 і її похідна
і її похідна
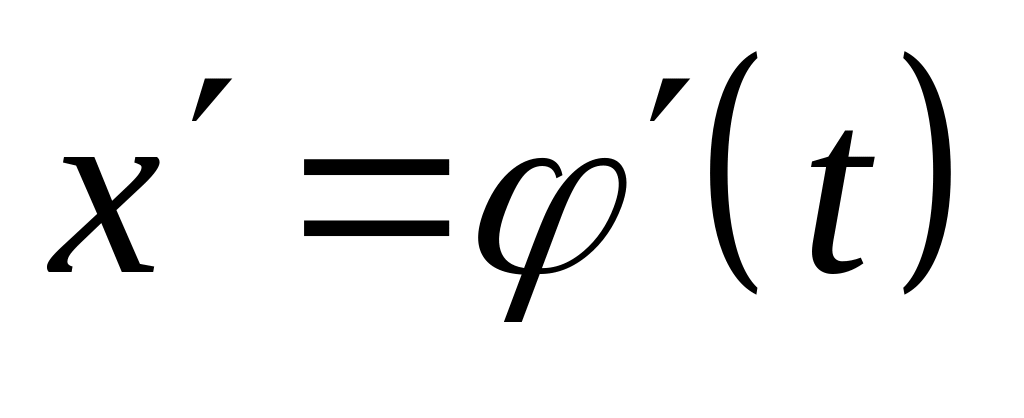 неперервні на відрізку
неперервні на відрізку
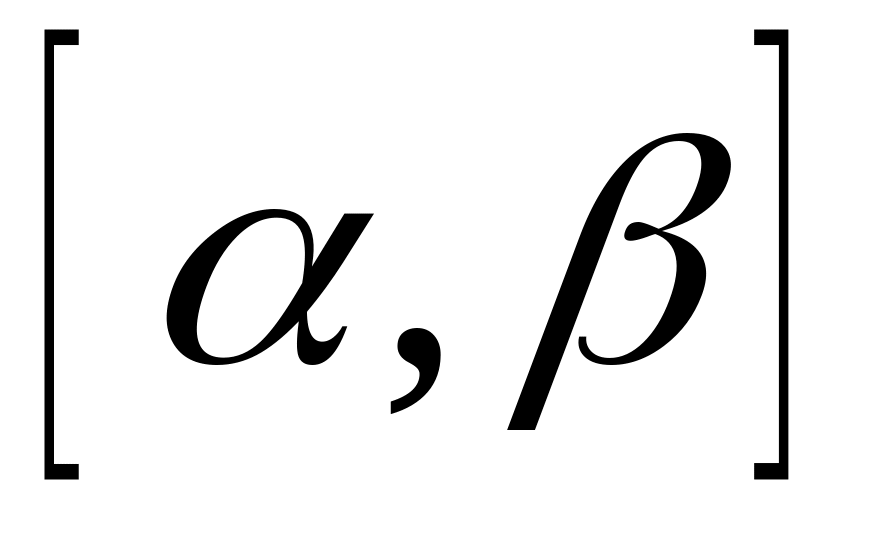 ;
;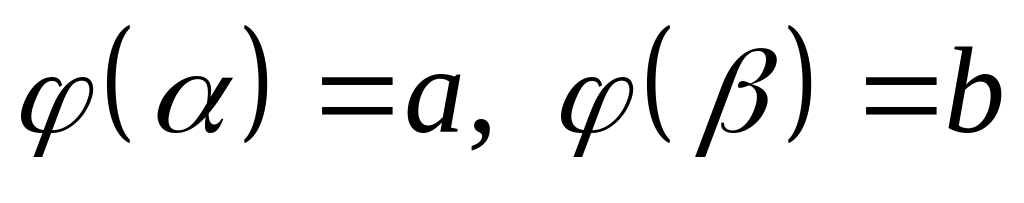 і
і
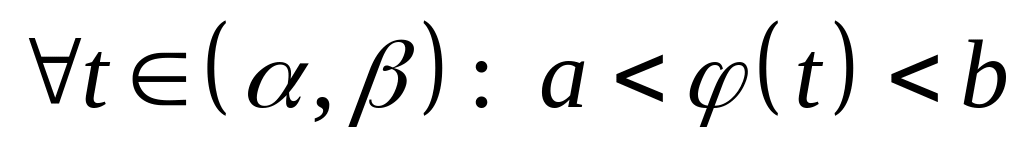 .
.
Тоді справджується рівність
 .
.
Метод інтегрування частинами
Теорема 2
Якщо функції
![]() мають на відрізку
неперервні похідні, то справедлива
формула
мають на відрізку
неперервні похідні, то справедлива
формула
![]() .
.
Ця формула називається формулою інтегрування частинами.
4. Застосування визначеного інтеграла
Обчислення площ плоских фігур .
Довжина дуги
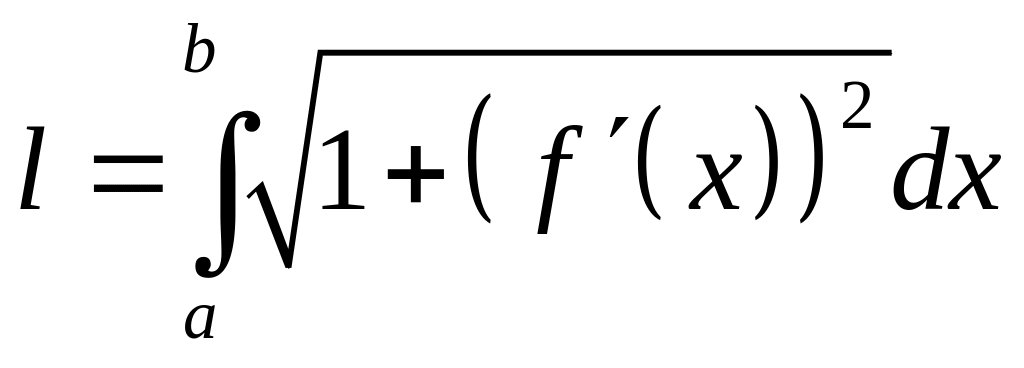 .
.Об’єм тіла
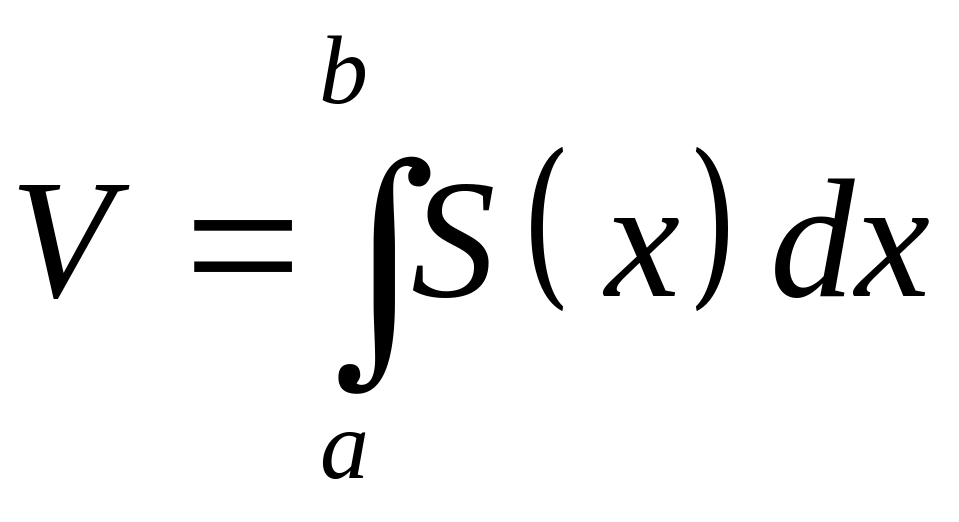 ,
де
,
де
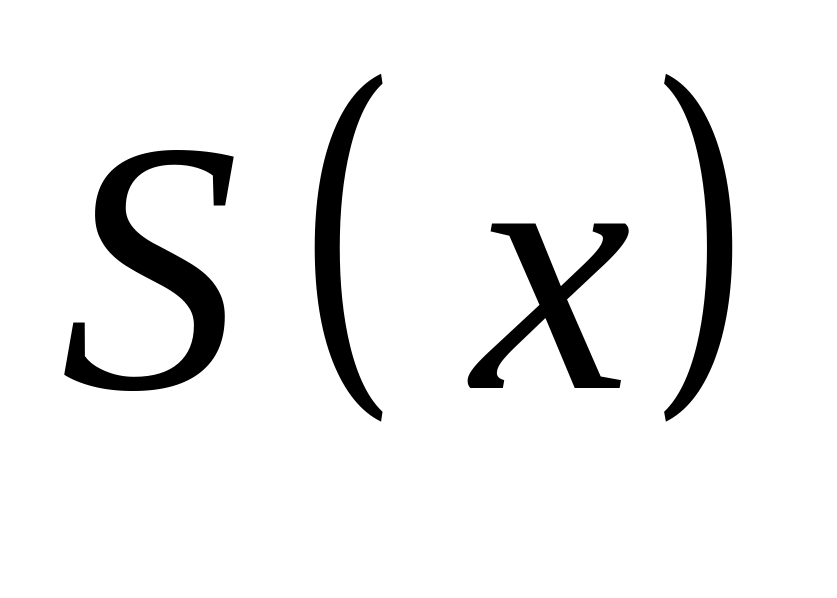 - площа перерізу.
- площа перерізу.Об’єм тіла обертання
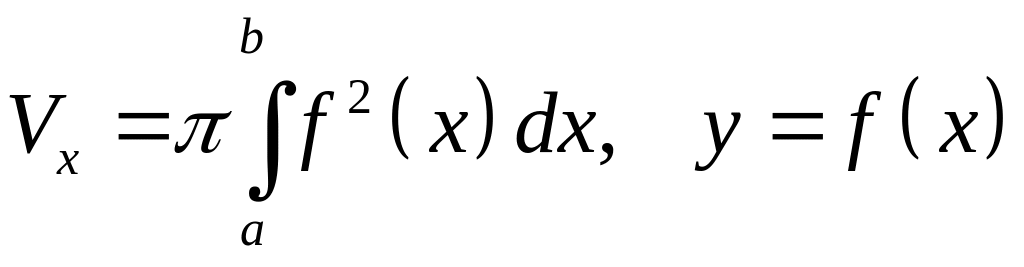 .
.Площа поверхні обертання
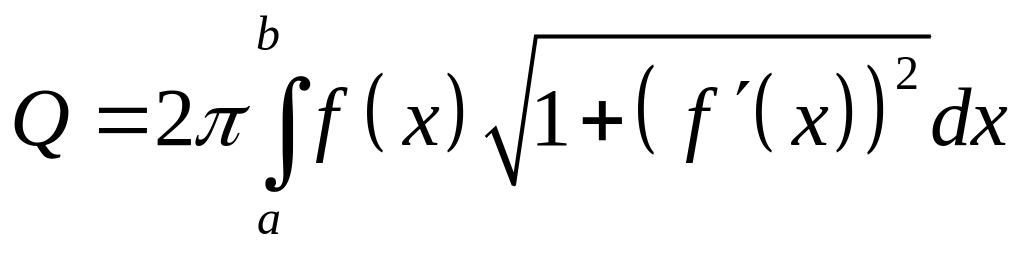 .
.
