Диференціал функції багатьох змінних

3. Повний диференціал функції та його застосування до обчислення функцій і похибок

4. Диференціали вищих порядків

1. Повний диференціал функції та його застосування до обчислення функцій і похибок

Якщо функція диференційовна в точці , то її повний приріст в цій точці можна подати у вигляді: , де при .

Повним диференціалом диференційовною в точці функції називається лінійна відносно та частина повного приросту цієї функції в точці , тобто .

Диференціалами незалежних змінних та назвемо прирости цих змінних , тоді повний диференціал можна записати:

;

.

Повний диференціал називають також головною частиною повного приросту диференційовної функції. При цьому виконується наближена рівність або

(1)

Рівність (1) ши­роко використовується в наближених обчисленнях, оскільки диферен­ціал функції обчислюється простіше, ніж її повний приріст.

За допомогою диференціала можна оцінити похибку в обчисленнях.

Нехай задана диференційована функція , незалежні змінні якої виміряні з точністю . Похибка, з якою обчислюється дорівнює величині

. (2)

Приклад 1. Знайти повний диференціал функції .

Приклад 2. Обчислити наближено за допомогою повного диференціала

.

Розглянемо функцію і застосуємо до неї формулу (2), поклавши .

.

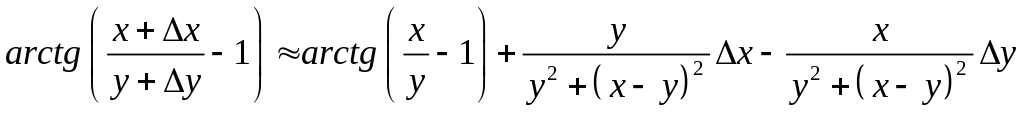
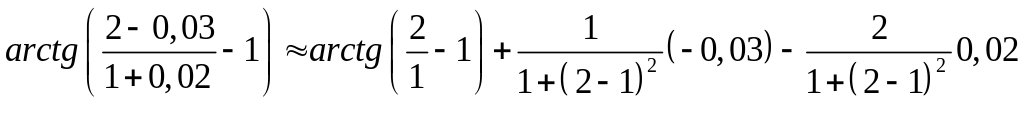
Приклад 3.

Знайти повний диференціал функції , обчислити його значення при х=2, у=1, =0,01, =0,02 і знайти абсолютну і відносну похибку наближення .

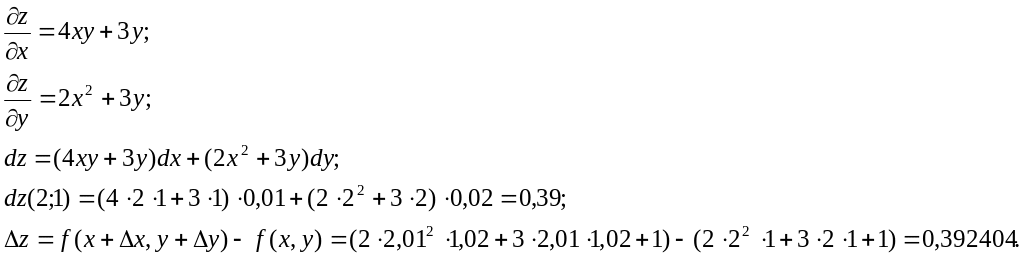
Абсолютна похибка .

Відносна похибка .

Приклад 4.

Знайти повний диференціал функції

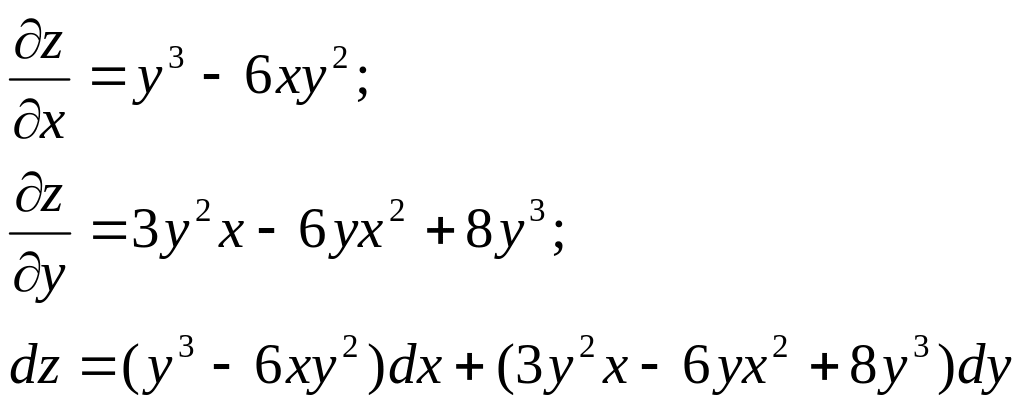
Приклад 5. Знайти значення повного диференціала функції , при .

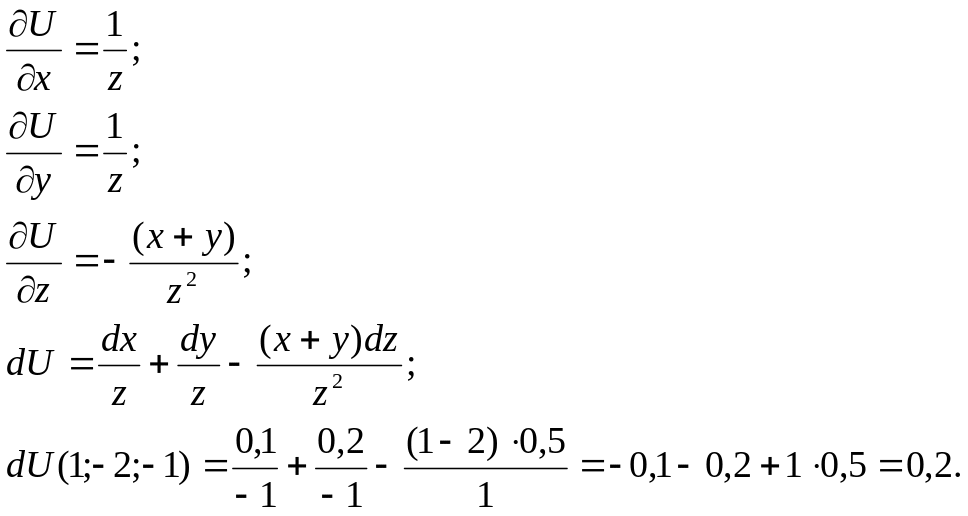
2. Диференціали вищих порядків

Повний диференціал функції називають диференціалом першого порядку.

Диференціал другого порядку визначають за формулою .

Тоді, якщо функція має неперервні частинні похідні, то

або .

Символічно це записують .

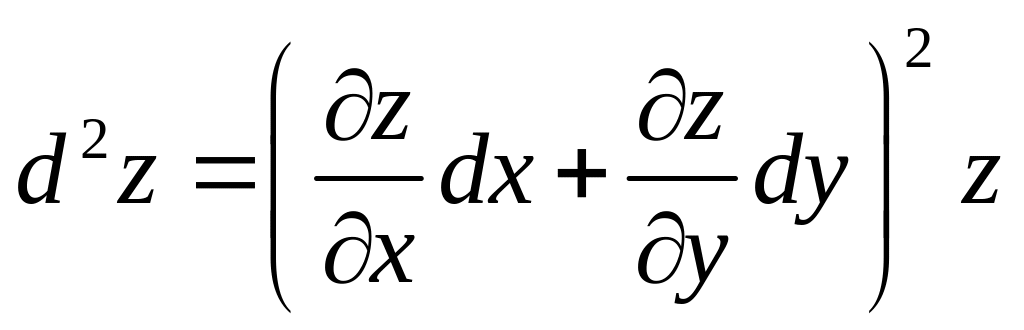Диференціал третього порядку .

Диференціал порядку .

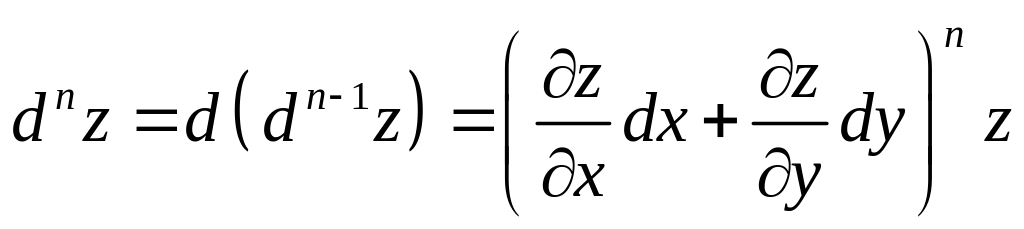Приклад 6. Знайти диференціал другого порядку функції .

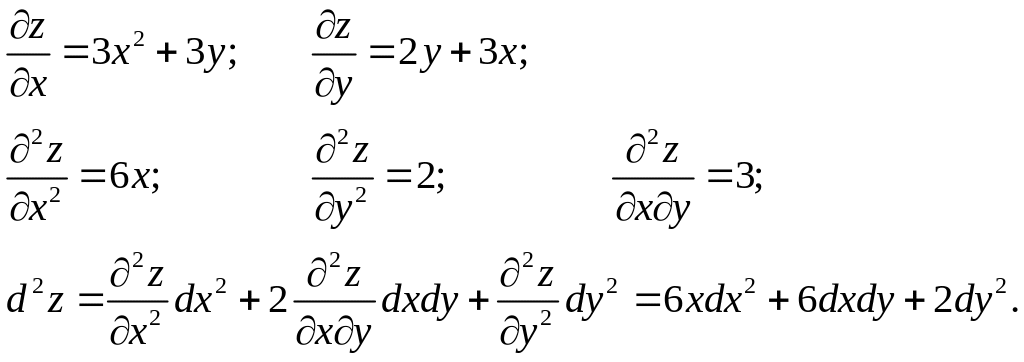
Правила диференціювання:

1.

2.

3.

4.

Локальні екстремуми функції багатьох змінних

1. Локальні екстремуми функції двох змінних

2. Найбільше та найменше значення функції

1. Локальні екстремуми функції двох змінних

Нехай функція z = f(х, у) визначена в області D, а точка D. Якщо існує окіл точки , який належить області D і для всіх відмінних від точок М цього околу виконується нерівність f (М)< f ( )(f (М) > f ( )), то точку називають точкою ло­кального максимуму (мінімуму) функції , а число – ло­кальним максимумом (мінімумом) цієї функції (рис. 1).

Рис. 1.

Точки максимуму та мінімуму функції називають її точками екстремуму.

Теорема 1 (необхідні умови екстремуму)

Якщо функція має в точці локальний екстремум, то в цій точці частин­ні похідні першого порядку по змінних х та у дорівнюють нулю або не існують.

Подібна теорема справедлива для функції n змінних. Точку , в якій частинні похідні першого порядку функції дорів­нюють нулю, тобто , називають стаціонарною точкою функції .

Стаціонарні точки та точки, в яких частинні похідні не існують, називаються критичними точками.

В задачах з практичним змістом, як правило, відомо, що функція має екстремум. Якщо така функція має лише одну критичну точку, то ця точка і буде точкою екстремуму.

Теорема 2 (достатні умови екстремуму)

Нехай в стаціонарній точці М (х ; у ) і деякому її околі функція має неперервні частинні похідні другого порядку. Якщо

>0,

то функція має в точці М екстремум, причому максимум при <0 і мінімум при >0. Якщо <0, то в точці М функція f (х, у) екстремуму не має.

Наслідок (другі достатні умови екстремуму)

Функція має мінімум в стаціонарній точці , якщо диференціал другого порядку в цій точці >0, і максимум – якщо <0.

Другі достатні умови екстремуму справедливі для функцій довільного числа змінних.

На основі теорем 1 і 2 дістанемо правило дослідження диференційовних функцій двох змінних на екстремум. Щоб знайти екстремум диференційовних функцій , необхідно:

1. Знайти стаціонарні точки функцій із системи рівнянь:

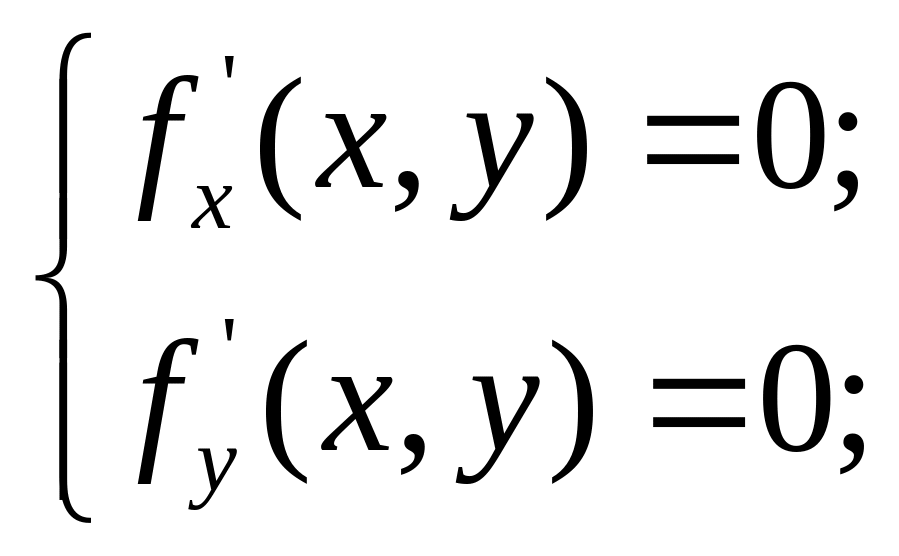
2. У кожній стаціонарній точці обчислити вираз , якщо >0, то – точка екстремуму функції, причому точка максимуму при <0 і мінімуму при >0; якщо <0, то точка (х ; у ) не є точкою екстремуму функції;

3. Обчислити значення функції в точках максимуму та мінімуму. Якщо =0, то ніякого висновок про характер стаціонарної точки зробити не можна і потрібне додаткове дослідження.

Приклад 1.

Знайти точки локального екстремуму функції

Знаходимо частинні похідні

Стаціонарні точки функції визначимо із системи:

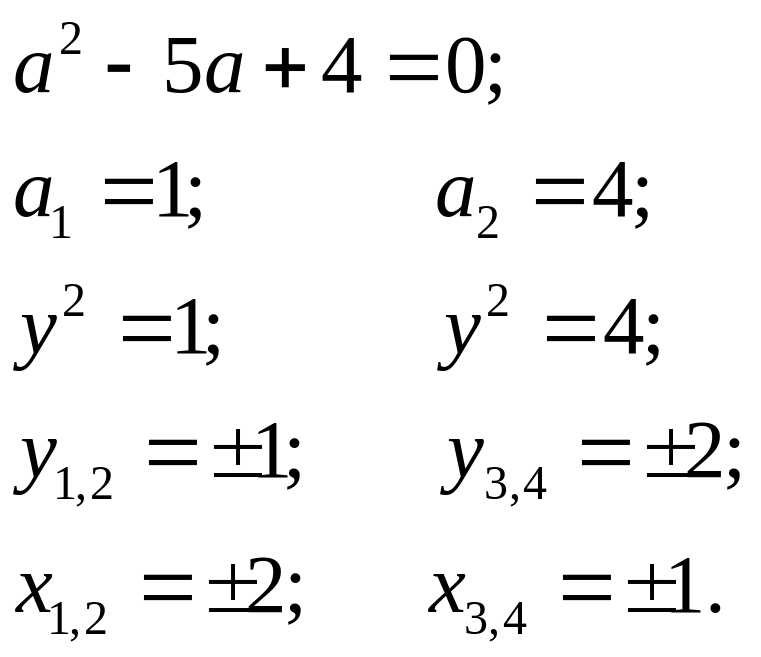
Отже, функція має 4 стаціонарні точки:

Знайдемо величину . Оскільки то

Обчислимо величину в кожній стаціонарній точці:

<0 – в т. немає екстремуму.

<0 – в т. немає екстремуму.

>0 – в т. функція має екстремум; >0, отже в т. функція має локальний мінімум:

>0 – в т. функція має екстремум; <0, отже в т. функція має локальний максимум:

Приклад 2.

Знайти стаціонарні точки функції .

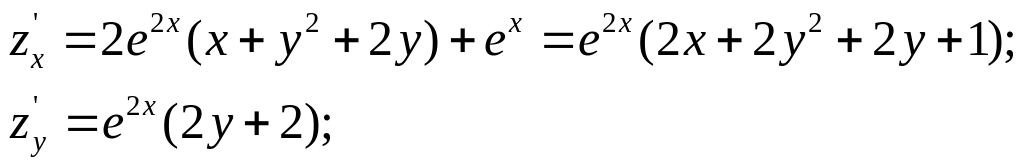
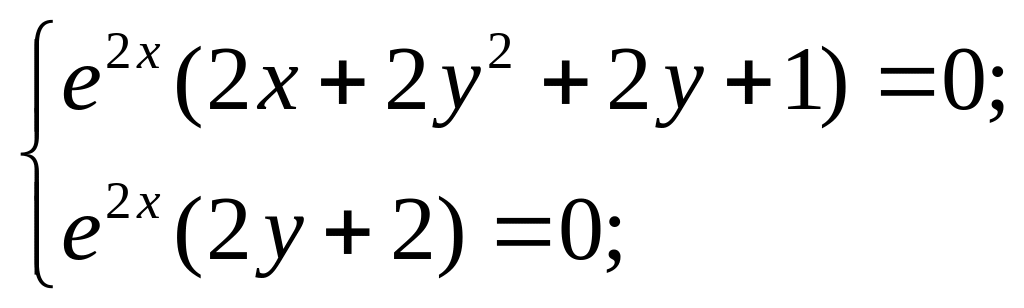
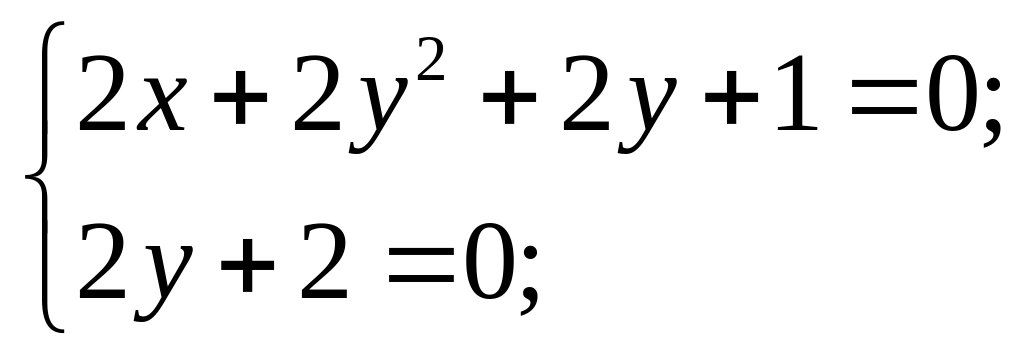
т. М(- ;-1) – стаціонарна точка.

Так як =0, то ніякого висновку про характер стаціонарної точки зробити не можна і потрібне додаткове дослідження.

2. Найбільше та найменше значення функції

Функція задана і неперервна в замкненій та обмеженій області , досягає свого найбільшого і наймен­шого значень. У внутрішніх точках області диференційовна функція може набувати цих значень лише в точках локального екстремуму.

Алгоритм знаходження найбільшого і наймен­шого значень:

1) Знайти всі стаціонарні точки функції, які належать області , розв’язавши систему рівнянь 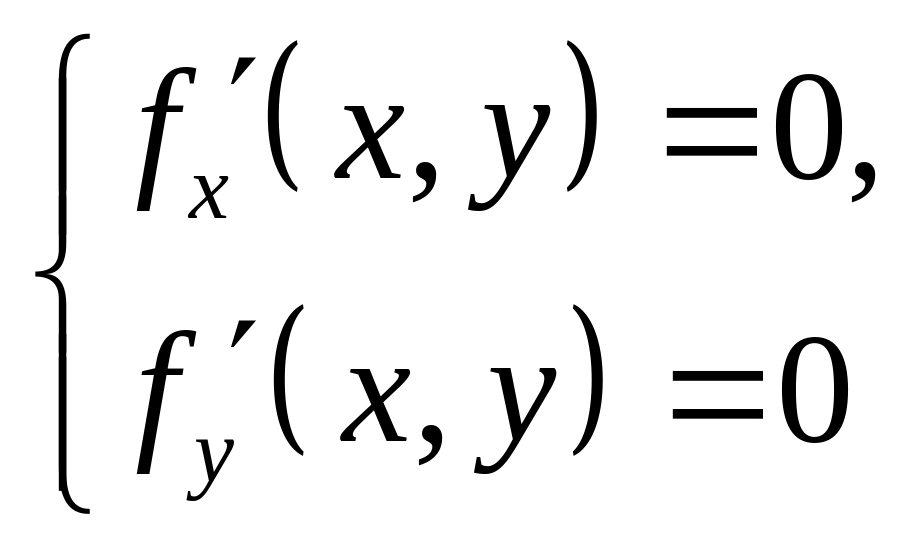і обчислити значення функції в цих точках.

2) Дослідити функцію на екстремум на межі області (знайти найбільше (найменше) значення функції на межі області ). Використовуючи рівняння межі, ця задача зводиться до знаходження абсолютного екстремуму функції однієї змінної.

3) Серед здобутих значень функції всередині і на межі області вибирають найбільше і найменше значення.

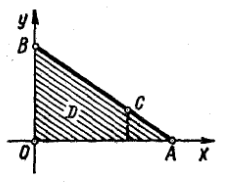
Приклад 3.

Знайти найбільше і найменше значення функції в області – трикутнику, обмеженому прямими х=0, у=0, х+у=6.

Знайдемо частинні похідні першого порядку:

Прирівнюючи похідні до нуля і скорочуючи їх на та (всередині трикутника ОАВ х≠0, у≠0) дістанемо систему рівнянь

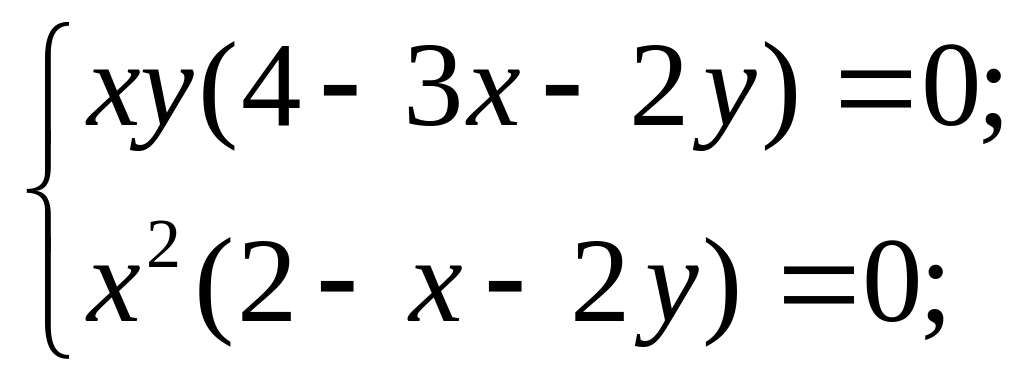
Стаціонарна точка належить область D, тому обчислюємо значення .

Рівняннями сторін ОВ та ОА трикутника є х=0 та у=0, тому значення функції z=0 в усіх точках відрізків ОВ та ОА, зокрема z(0)= z(А)= z(В)=0.

Знайдемо стаціонарні точки на стороні АВ трикутника ОАВ. Рівняння цієї сторони у=6-х, тому z= .

Далі дістанемо:

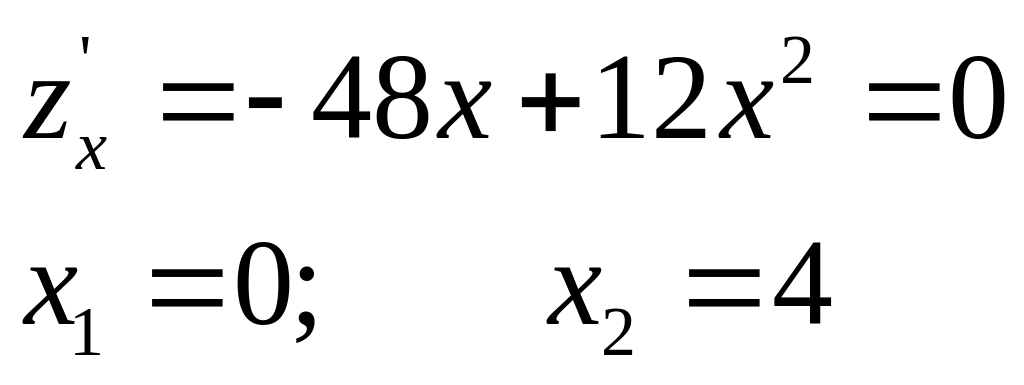
Оскільки у=6-х, то ,

Знаходимо точки В(0;6) і С(4;2) і обчислюємо значення z(С)=-128.

Порівнюючи значення заданої функції в точках А, В, С, О, М, знаходимо найбільше й найменше значення:

Приклад 4.

Знайти екстремум функції

Знаходимо частинні похідні

Стаціонарні точки функції визначимо із системи:

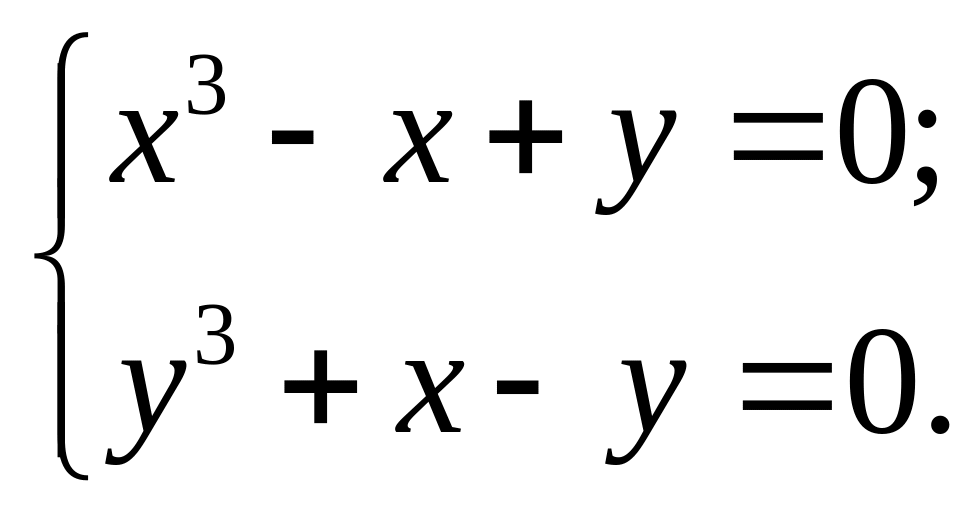
Додаючи ці рівняння, знайдемо: звідки у= -х. Підставляючи у= -х в перше рівняння системи, дістанемо

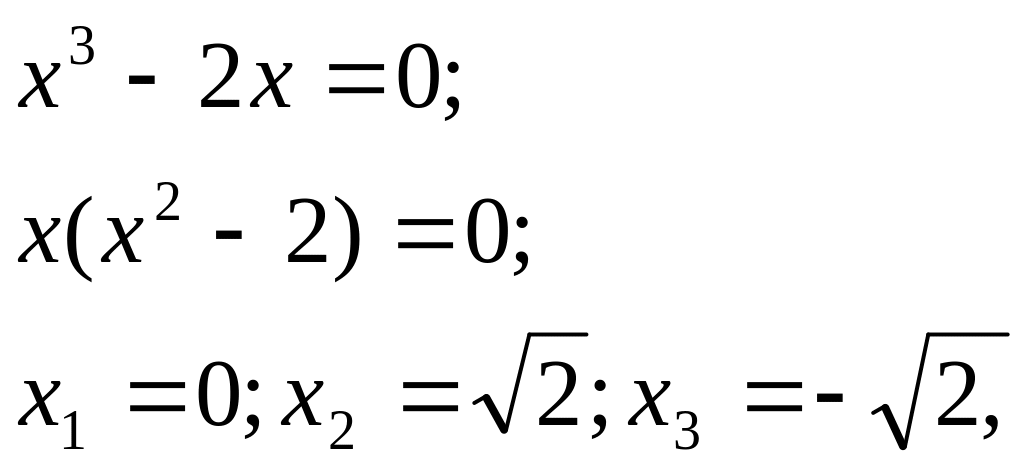
тоді

Отже, функція має три стаціонарні точки: М (0;0), М ( ; - ), М (- ; ).

Знайдемо величину . Оскільки

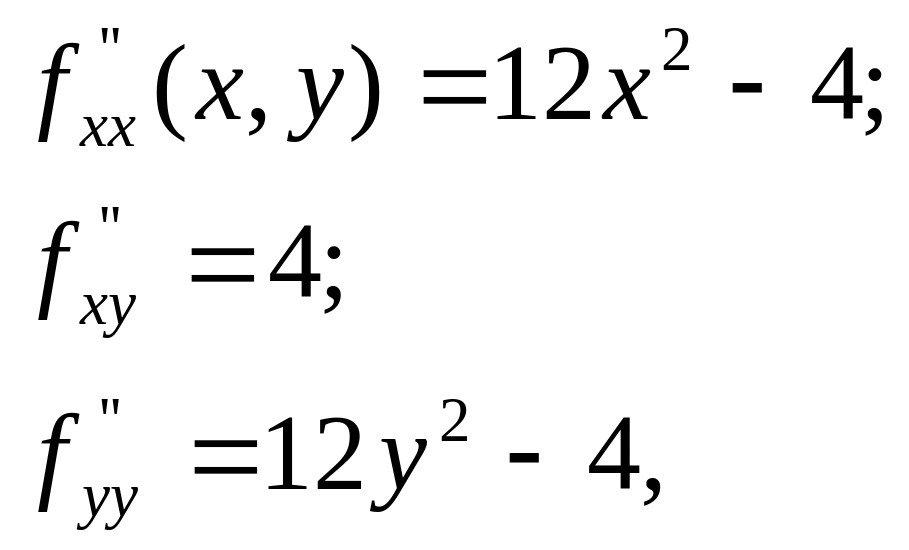
то

Обчислимо величину в кожній стаціонарній точці: (М )=0, (М )= (М )=384>0, >0.

Таким чином, точки та - точки мінімуму. В цих точках

В точці М значення (М )=0, тому теорему 2 застосовувати не можна. Переконаємось, що в точці екстремум відсутній. Дійсно, якщо у=0, то <0 в околі точки М значення можуть бути як додатні, так і від’ємні, а це значить, що точка М не є екстремальною. Відзначимо, що інших екстремумів задана функція не має, оскільки, точки, в яких похідні і не існують, відсутні.