
- •Визначники
- •1. Визначники другого та третього порядків
- •2. Властивості визначників
- •3. Розклад визначника за елементами рядка або стовпця
- •4. Поняття про визначники вищих порядків
- •Матриці
- •Системи лінійних рівнянь
- •Функція багатьох змінних, її границя та неперервність
- •Лекція №2. Частинні похідні функції багатьох змінних. Диференційовність функції багатьох змінних.
- •Диференціал функції багатьох змінних
- •Локальні екстремуми функції багатьох змінних
- •Умовний екстремум функції багатьох змінних
- •Диференціальне числення функції багатьох змінних
- •Визначений інтеграл
- •Диференціальні рівняння першого порядку
Диференціальні рівняння першого порядку
Основні поняття про диференціальні рівняння першого порядку
Диференціальні рівняння першого порядку з відокремлюваними змінними
Однорідні диференціальні рівняння першого порядку
Лінійні диференціальні рівняння першого порядку
1. Основні поняття про диференціальні рівняння. Задача Коші
Диференціальним рівнянням першого порядку називається рівняння виду
![]() ,
, ![]()
яке зв’язує
незалежну змінну
,
невідому функцію
![]() та її похідну
та її похідну
![]() .
.
Рівняння може не містити явно або , але обов’язково має містити похідну .
Диференціальне рівняння , нерозв’язане відносно похідної називається неявним.
Якщо рівняння можна розв’язати відносно , то його записують у вигляді
![]()
![]()
і називають рівнянням першого порядку, розв’язаним відносно похідної.
Рівняння можна записати
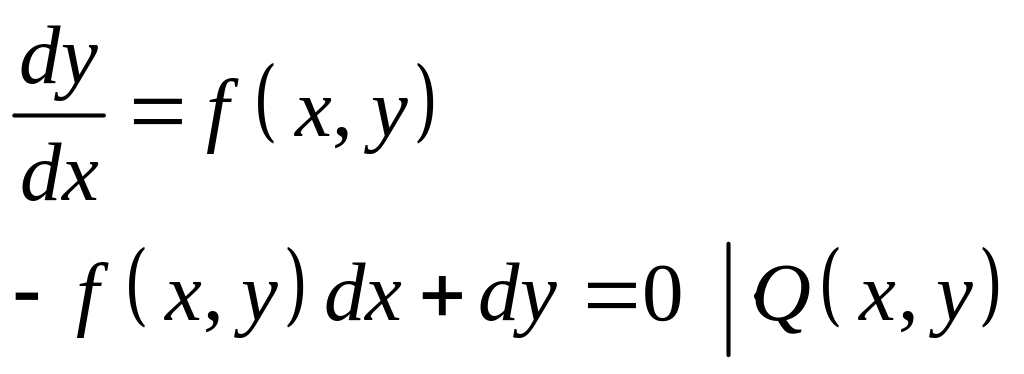
![]() ,
, ![]()
де
![]() – відомі функції. Змінні
– відомі функції. Змінні
![]() в рівняння
рівноправні.
в рівняння
рівноправні.
Знаходження невідомої функції, що входить у диференціальне рівняння називається розв’язанням або інтегруванням цього рівняння.
Розв’язком
диференціального рівняння
на
деякому інтервалі
![]() називається
диференційована на цьому інтервалі
функція
називається
диференційована на цьому інтервалі
функція
![]() ,
яка при підстановці в рівняння
обертає його в тотожність по
на
,
тобто
,
яка при підстановці в рівняння
обертає його в тотожність по
на
,
тобто
![]()
Графік розв’язку диференціального рівняння називається інтегральною кривою цього рівняння.
Теорема Коші (про існування і єдиність розв’язку)
Нехай функція
і її частинна похідна
![]() визначені
і неперервні у відкритій області
визначені
і неперервні у відкритій області
![]() площини
площини
![]() і точка
і точка
![]() .
Тоді існує єдиний розв’язок
рівняння
,
який задовольняє умову
при
,
тобто
.
Тоді існує єдиний розв’язок
рівняння
,
який задовольняє умову
при
,
тобто
![]() .
.
Задача знаходження
розв’язку рівняння
,
який задовольняє початкову умову
![]() або
або
![]() називається задачею
Коші.
називається задачею
Коші.
Функція
![]() ,
яка залежить від аргументу
і довільної сталої
називається загальним
розв’язком
рівняння
в області
,
якщо вона задовольняє умови:
,
яка залежить від аргументу
і довільної сталої
називається загальним
розв’язком
рівняння
в області
,
якщо вона задовольняє умови:
функція
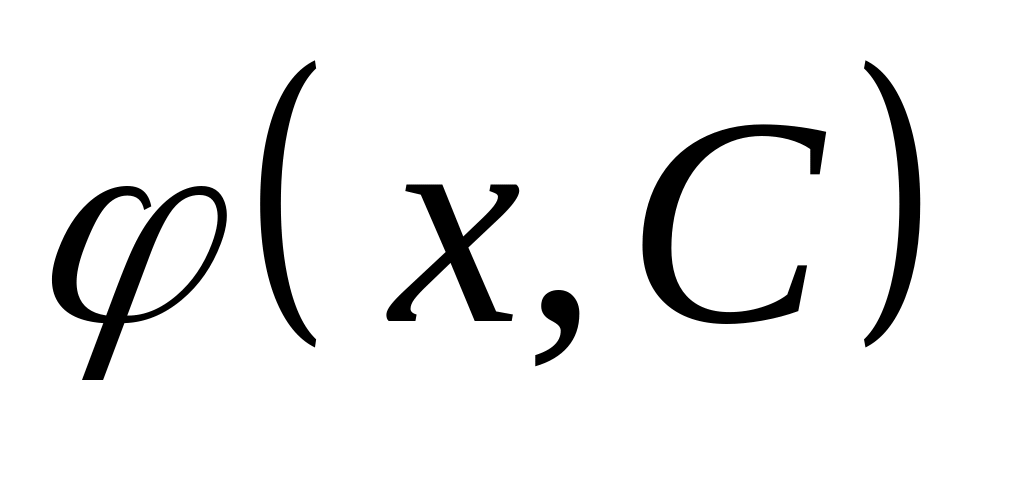 є розв’язком рівняння при будь-якому
значенні
з деякої множини;
є розв’язком рівняння при будь-якому
значенні
з деякої множини;для довільної точки можна знайти таке значення
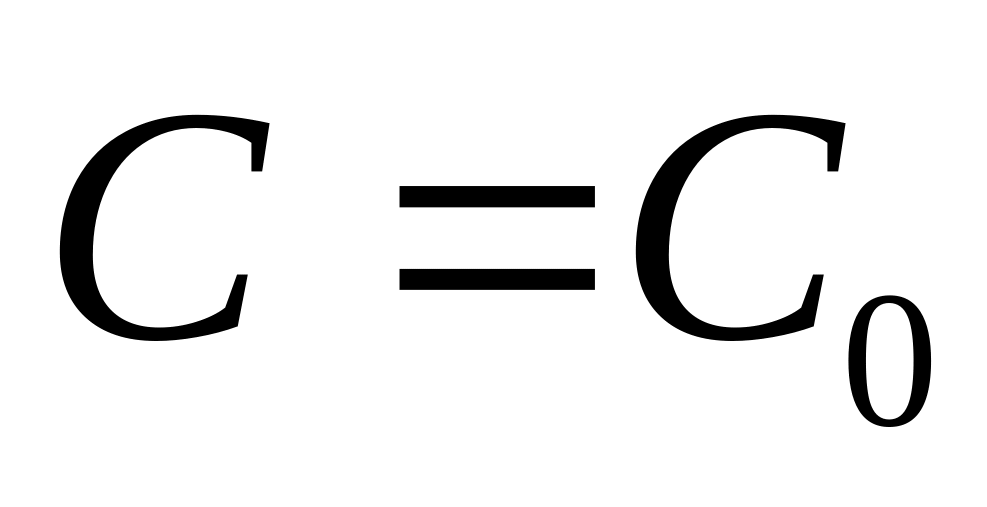 ,
що функція
,
що функція
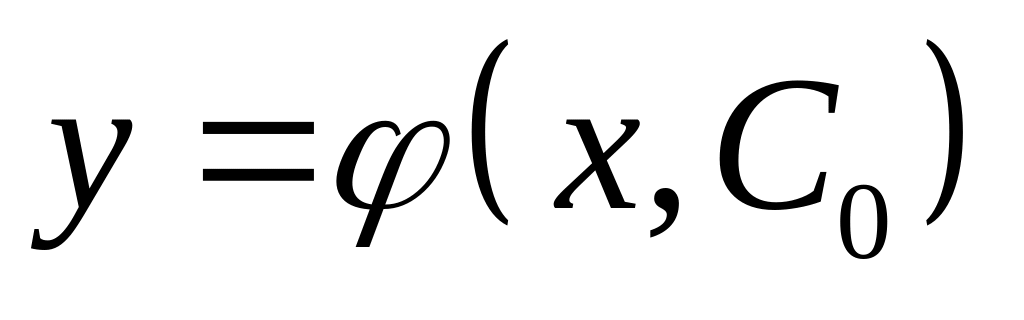 задовольняє початкову умову
задовольняє початкову умову
 .
.
Частинним розв’язок рівняння називається функція , яка утворюється із загального розв’язку при певному значенні сталої .
Якщо загальний
розв’язок диференціального рівняння
знайдено у неявному вигляді, тобто
![]() ,
то його називають загальним
інтегралом
диференціального рівняння.
,
то його називають загальним
інтегралом
диференціального рівняння.
Рівність
![]() називається частинним
інтегралом
диференціального рівняння.
називається частинним
інтегралом
диференціального рівняння.
2. Диференціальні рівняння першого порядку з відокремлюваними змінними
Рівняння виду
![]() ,
,
![]() де
де
![]() - задані і неперервні на деякому інтервалі
функції, називається диференціальним
рівнянням з відокремлюваними змінними.
- задані і неперервні на деякому інтервалі
функції, називається диференціальним
рівнянням з відокремлюваними змінними.
![]()
![]()
![]()
Диференціальне
рівняння виду
,
в якому множник при
![]() є
функцією яка залежить лише від
,
а множник при
є
функцією яка залежить лише від
,
а множник при
![]() є
функцією, яка залежить лише від
,
називається диференціальне рівняння
з відокремленими змінними.
є
функцією, яка залежить лише від
,
називається диференціальне рівняння
з відокремленими змінними.
![]()
Приклад 1.
Розв’язати
рівняння
![]()
Розглянемо рівняння
![]() ,
, ![]()
де
![]() - задані числа.
- задані числа.
Введемо заміну:
![]() .
.
![]()
![]()
Підставимо у рівняння :
![]()
![]()
![]()
Інтегруючи це
рівняння і замінюючи
на
![]() ,
дістанемо загальний інтеграл рівняння
.
,
дістанемо загальний інтеграл рівняння
.
Приклад 2.
Розв’язати
рівняння
![]()
3. Однорідні диференціальні рівняння першого порядку
Функція
називається однорідною функцією n-го
виміру відносно змінних
та
,
якщо для довільного числа
![]() виконується тотожність
виконується тотожність
![]()
1)
![]() – однорідна функція другого виміру,
– однорідна функція другого виміру,
![]() .
.
2)
![]() – однорідна функція нульового виміру,
– однорідна функція нульового виміру,
![]() .
.
Диференціальне рівняння називається однорідним, якщо функція є однорідною функцією нульового виміру.
Однорідні рівняння
зводяться до рівнянь з відокремлюваними
змінними підстановкою
![]() ,
де
,
де
![]() – невідома функція.
– невідома функція.
![]()
![]()
![]()
Розв’язавши
рівняння
,
знайдемо
![]() ,
а потім функцію
.
,
а потім функцію
.
Приклад 3.
Розв’язати
рівняння
![]()
Розглянемо рівняння, які можна звести до однорідних
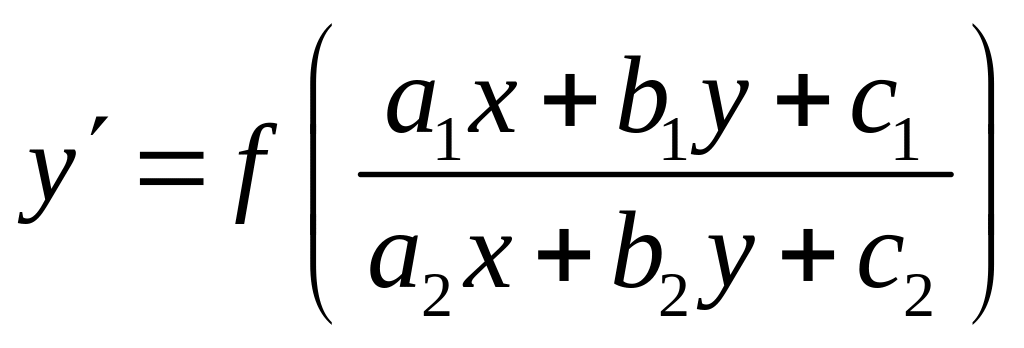
![]()
Можливі такі випадки:
якщо
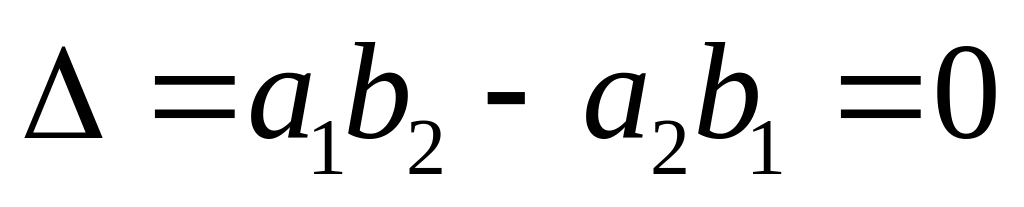 ,
то підстановкою
,
то підстановкою
 рівняння
зводиться до рівняння з відокремлюваними
змінними;
рівняння
зводиться до рівняння з відокремлюваними
змінними;якщо
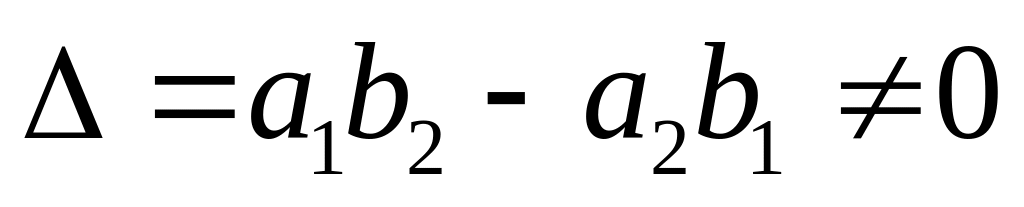 ,
то заміна
,
то заміна
 ,
і
,
і
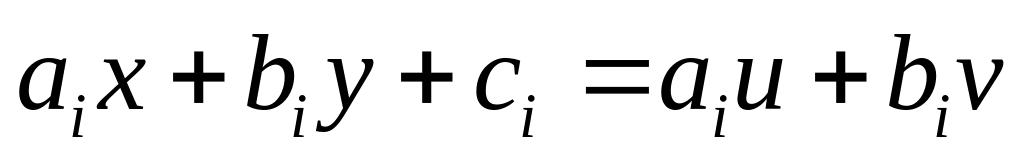 ,
,
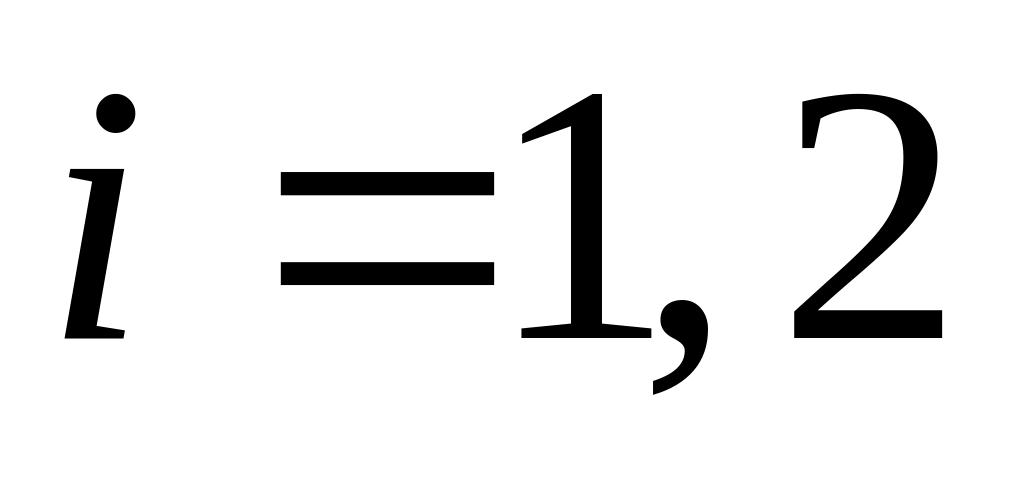 отримаємо однорідне рівняння.
отримаємо однорідне рівняння.
Приклад 4.
Розв’язати рівняння
![]()
4. Лінійні диференціальні рівняння першого порядку
Лінійним
диференціальним рівнянням першого
порядку
називається рівняння виду ![]() ,
,
![]()
де
![]() – задані і неперервні на деякому проміжку
функції.
– задані і неперервні на деякому проміжку
функції.
Метод Бернуллі
Розв’язок рівняння
шукають у вигляді добутку
![]() ,
де
,
де
![]() – невідомі функції.
– невідомі функції.
![]()
Підставимо похідну у рівняння :
![]()
![]()
Візьмемо функцію
![]() з умови
з умови
![]()
![]()
![]()
![]()
Візьмемо функцію
![]() з умови
з умови
![]()
![]()
![]()
![]()
![]()
Знайдемо функцію
![]()
Приклад 5.
Розв’язати
рівняння
![]() .
.
