4. Поняття про визначники вищих порядків

Визначник п-го порядку дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їхні алгебраїчні доповнення. Всі розглянуті вище властивості визначників третього порядку справджуються для визначників будь-якого порядку.

Розглянемо, наприклад, визначник четвертого порядку

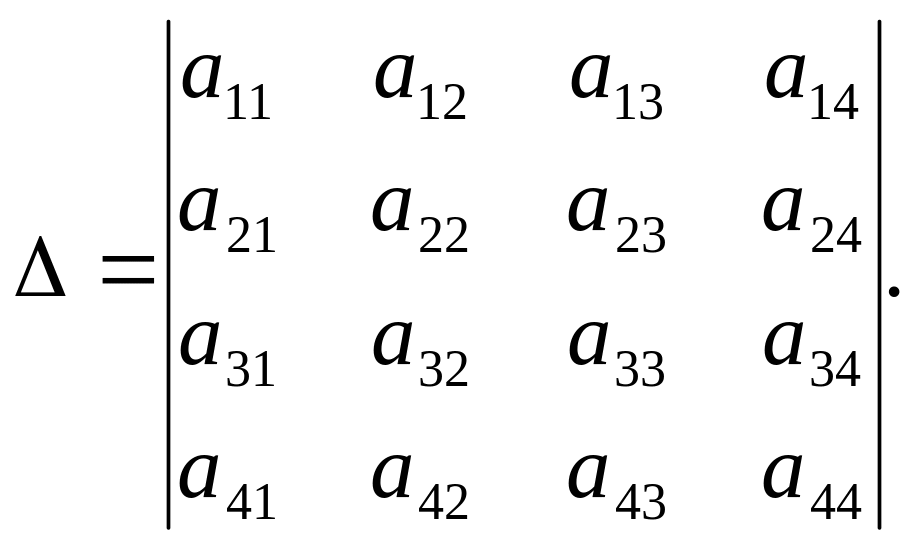
Цей визначник можна розкласти за елементами будь-якого рядка, наприклад першого:

(4)

Оскільки всі алгебраїчні доповнення у формулі (4) є визначники третього порядку, то цією формулою можна користуватись для обчислення визначника четвертого порядку. Але такий спосіб обчислення громіздкий: якщо для знаходження визначника четвертого порядку треба обчислювати чотири визначника третього порядку, то для знаходження визначника п’ятого порядку вже прийдеться обчислювати двадцять визначників третього порядку! Тому на практиці спочатку за допомогою властивості 8 перетворюють визначник так, щоб у деякому рядку чи стовпці всі елементи, крім одного, стали нулями. Розкладаючи тоді визначник згідно з теоремою за елементами цього рядка, дістанемо тільки один доданок, тому що всі ці інші доданки є добутками алгебраїчних доповнень на нуль.

Визначник порядку

,

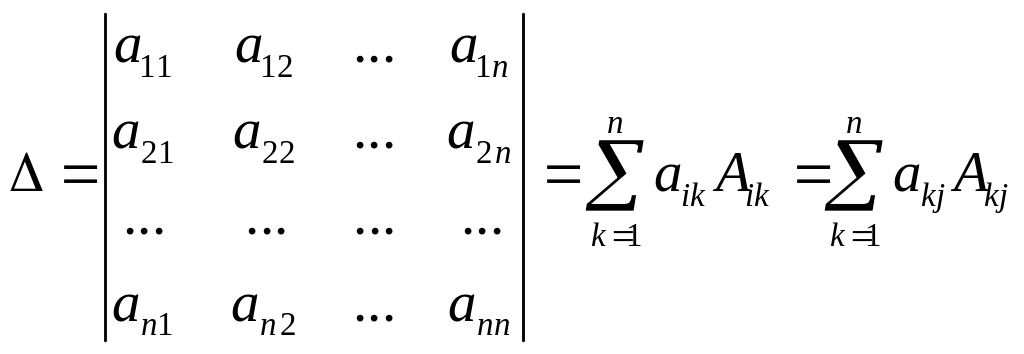де , – алгебраїчні доповнення елементів . Це розклад визначника за елементами рядка та стовпця.

Матриці

1. Означення матриці. Види матриць

2. Дії над матрицями та їх властивості

3. Обернена матриця

4. Ранг матриці

1. Означення матриці. Види матриць

Прямокутна таблиця чисел складена з т рядків та п стовпців і записана у вигляді

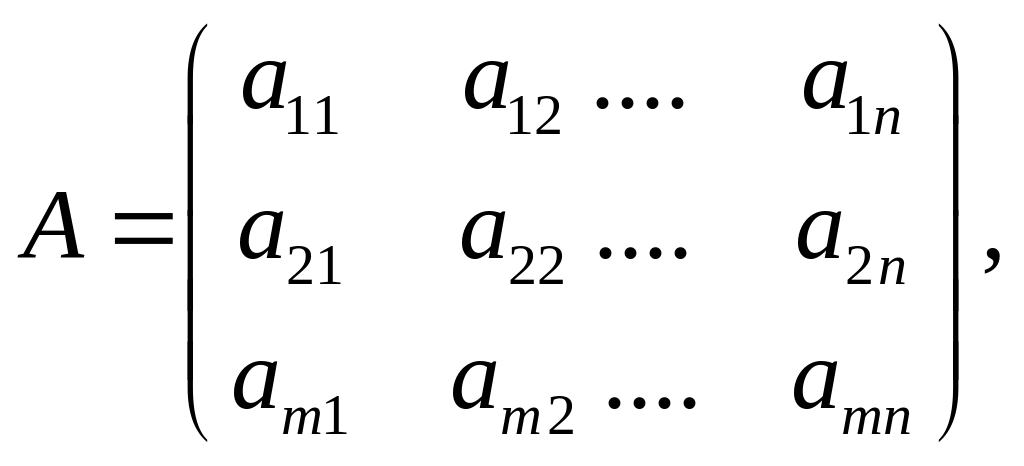
називається матрицею. Поняття матриці вперше ввели англійські математики У. Гамільтон і Д. Келі. Коротко матрицю позначають так: ,

де – елементи матриці, причому індекс і в елементі означає номер рядка, а - номер стовпця, на перетині яких стоїть даний елемент.

Добуток числа рядків т на число стовпців п називають розміром матриці і позначають . Записують розмір матриці:

Матриця, в якої число рядків дорівнює числу стовпців, називається квадратною. Кількість рядків (стовпців) квадратної матриці називається її порядком. Матриця, у якої всього один рядок, називається матрицею-рядком, а матриця, у якої всього один стовпець, матрицею-стовпцем.

Дві матриці та називаються рівними, якщо вони однакових розмірів і мають рівні відповідні елементи:

Нульовою називається матриця, у якої всі елементи дорівнюють нулю. Позначається така матриця буквою О. В квадратних матрицях виділяють головну і побічну діагональ.

Квадратна матриця називається діагональною, якщо всі її елементи, крім тих, що знаходяться на головній діагоналі, дорівнюють нулю.

Діагональна матриця, у якої кожен елемент головної діагоналі дорівнює одиниці, називається одиничною і позначається буквою Е. Наприклад, одинична матриця третього порядку має вигляд

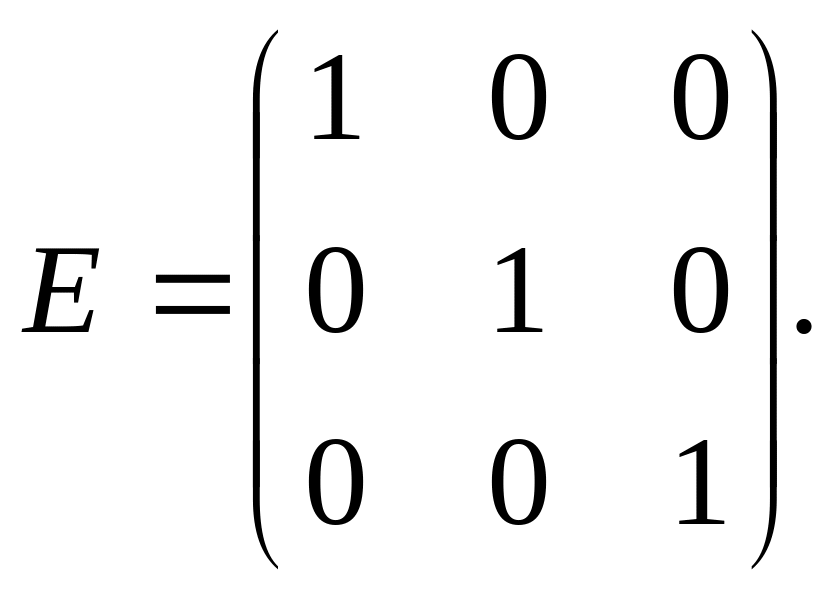
Будь-якій квадратній матриці

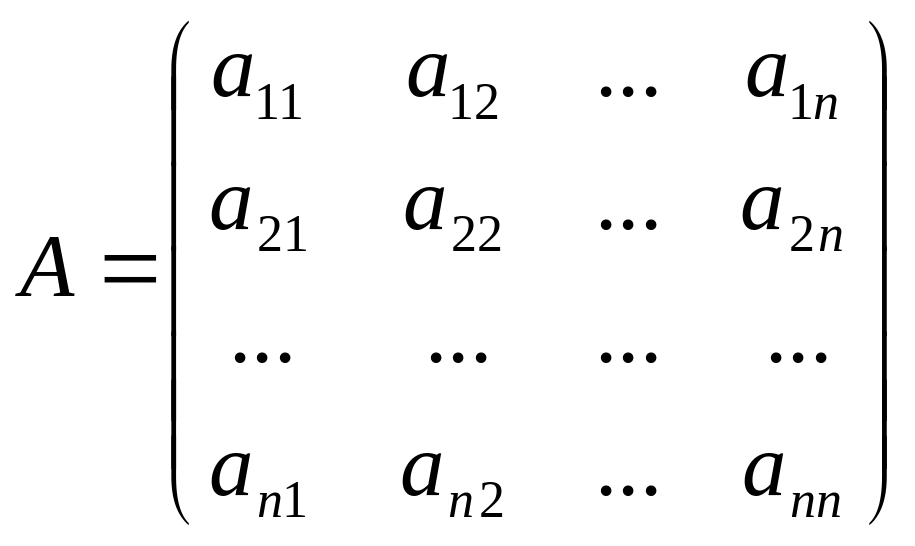
можна поставити у відповідність певне число, яке називається визначником (детермінантом) цієї матриці і позначається символом det A. За означенням

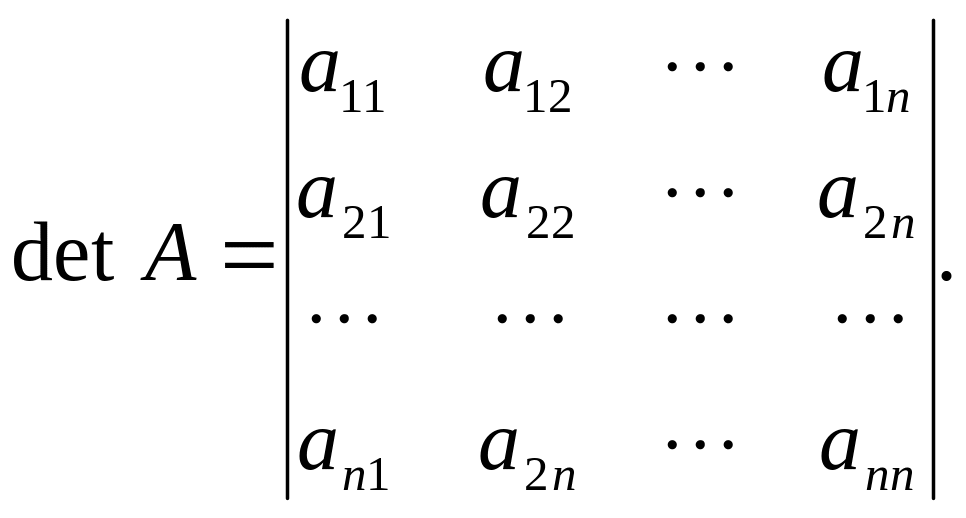
Прямокутна матриця розміром визначника не має.

2. Дії над матрицями та їх властивості

1. Операція додавання матриць вводиться тільки для матриць однакового розміру. Сумою С = А + В двох матриць називається матриця

2. Добутком матриці на число (або число на матрицю називається матриця .

3. Різниця матриць А – В визначається як сума матриць А і матриці В, помноженої на -1:

Властивості операцій:

а) А + В = В + А – комутативність відносно додавання матриць;

б) А + (В + С) = (А + В) + С – асоціативність відносно додавання матриць;

в) А + О = А; А – А = О – роль нульової матриці в діях на матрицями така, як і числа нуль в діях над числами;

г) – асоціативність відносно множення чисел;

д) – дистрибутивність множення на число відносно додавання матриць;

е) – дистрибутивність множення на матрицю відносно додавання чисел.

4. Операція множення двох матриць вводиться лише для узгоджених матриць. Матриця А називається узгодженою з матрицею В, якщо кількість стовпців першої матриці А дорівнює кількості рядків другої матриці В.

Якщо ця умова не виконується, тобто матриці неузгоджені, то множення таких матриць неможливе.

З узгодженості матриці А з В не випливає , взагалі кажучи, узгодженість матриці В з А.

Квадратні матриці одного порядку взаємно узгоджені.

Добутком С = АВ матриці на матрицю називається така матриця, у якої елемент дорівнює сумі добутків елементів і-го рядка матриці А на відповідні елементи j-го стовпця матриці В:

це означення називають правилом множення рядка на стовпець.

З правила множення матриць випливає, що завжди можна перемножити дві квадратні матриці одного порядку; в результаті дістанемо матрицю того самого порядку. Зокрема, квадратну матрицю можна помножити саму на себе, тобто піднести до квадрата; прямокутну неквадратну матрицю піднести до квадрата не можна.

Операція множення матриць не комутативна, тобто при множені матриць не можна міняти місцями множники:

Наприклад (перевірте):

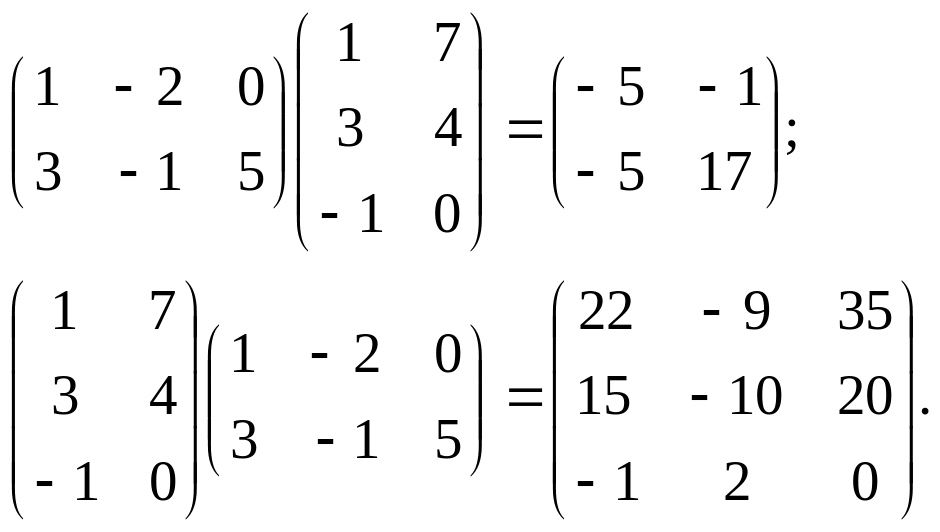
Властивості дій над матрицями (за умови, що вказані операції мають зміст):

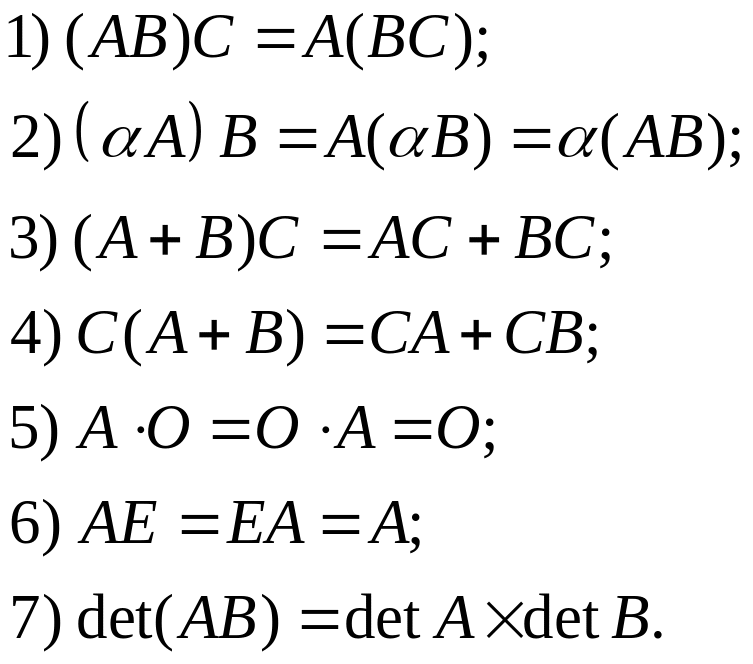
3. Обернена матриця

Нехай А – квадратна матриця. Матриця називається оберненою до матриці А, якщо виконується умова:

Квадратна матриця А називається виродженою, якщо і невиродженою, якщо

Нехай тоді матриця А має обернену матрицю А^-1, причому

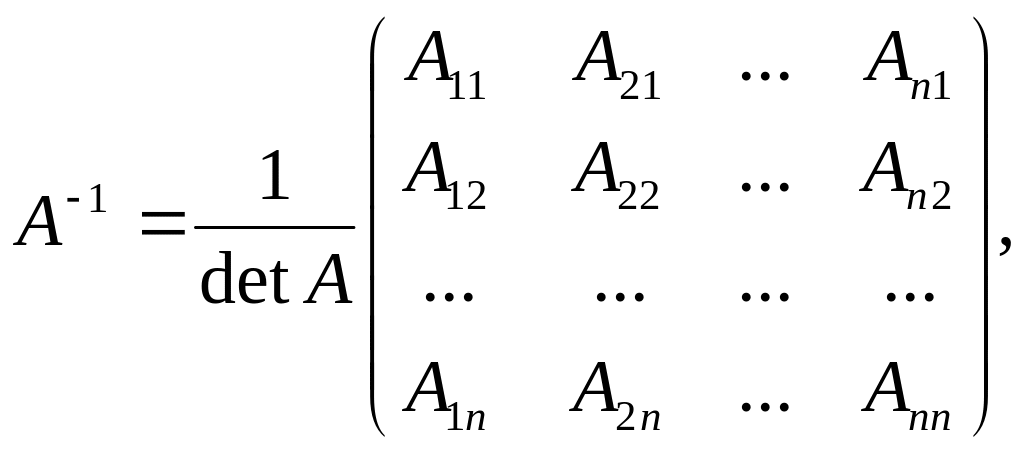(1)

де - алгебраїчні доповнення елементів визначника матриці

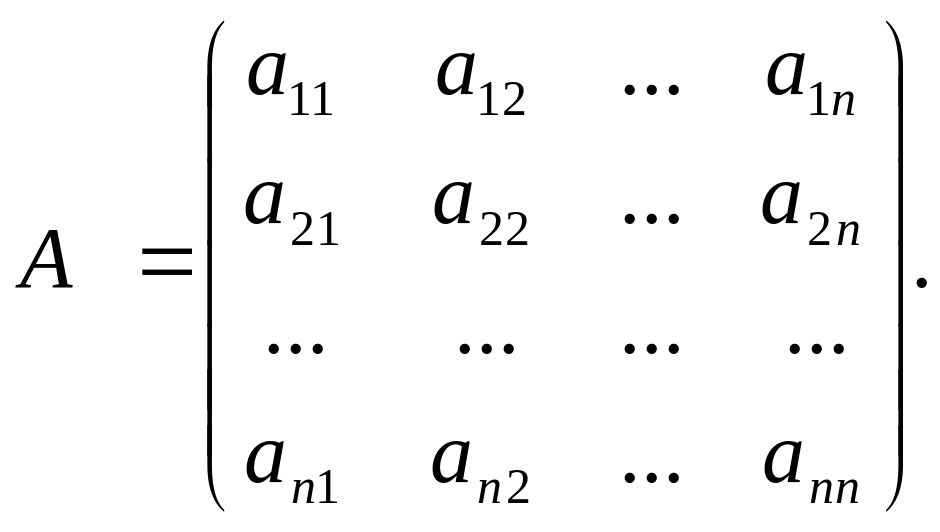
Теорема.

Для існування оберненої матриці необхідно і достатньо, щоб матриця А була невиродженою.

Приклад 1.

Знайти матрицю обернену до матриці

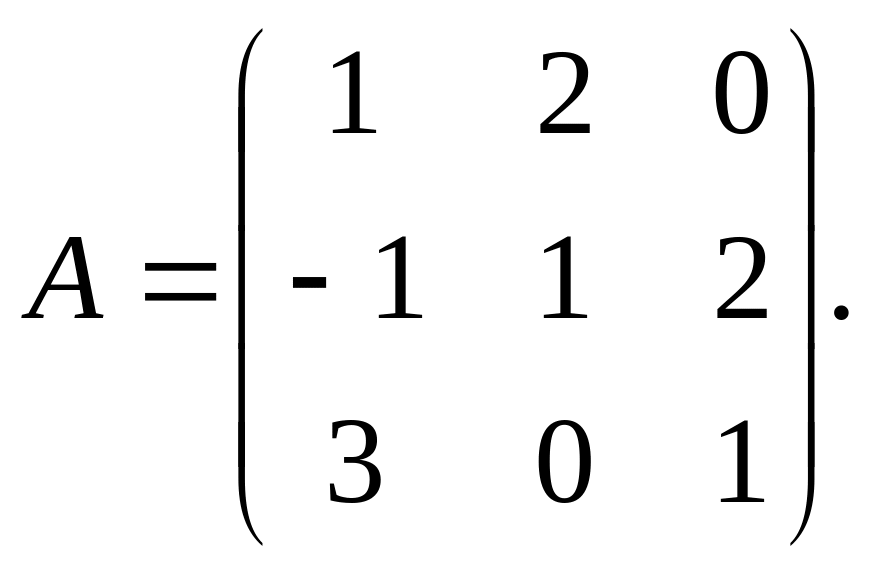
Обчислимо визначник матриці А:

Матриця А невироджена, тому обернена матриця знаходиться за формулою (1). Знаходимо алгебраїчні доповнення всіх елементів даної матриці:

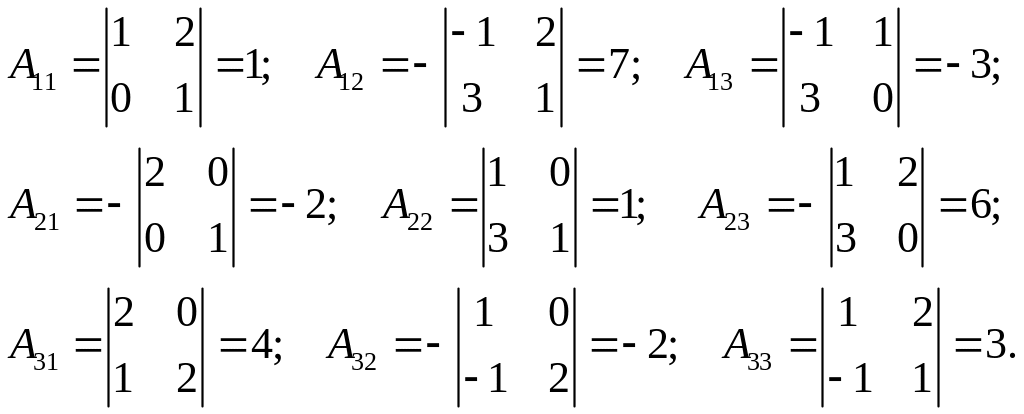
Складаємо обернену матрицю

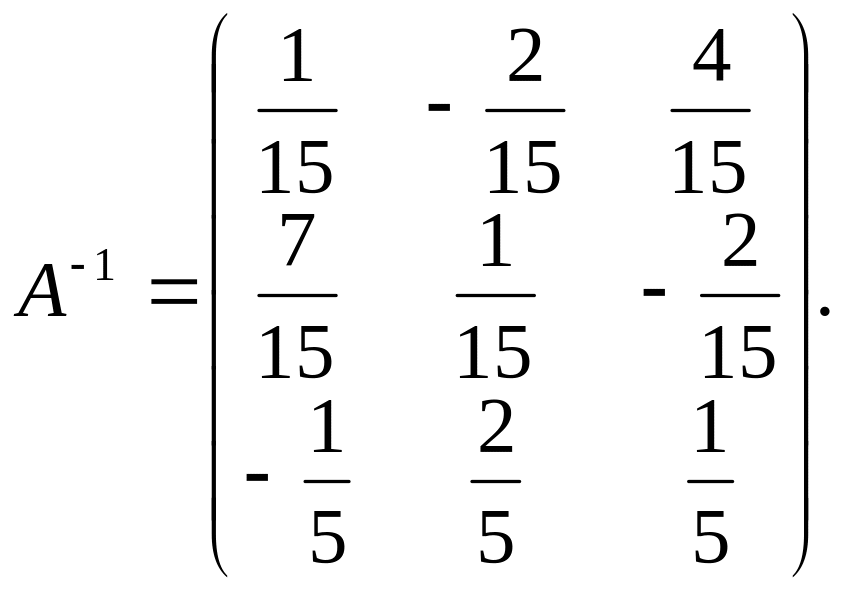
Переконуємось, що

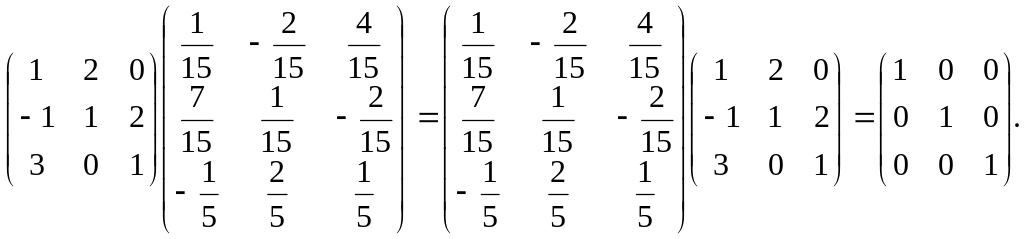
4. Ранг матриці

Нехай задано матрицю Виділимо в матриці А будь-які рядків і стільки ж стовпців, де - число, не більше чисел т і п, тобто

Визначник порядку , складений з елементів, що стоять на перетині виділених рядків і стовпців, називається мінором -го порядку матриці А.

Рангом r(А) матриці А називається найбільший з порядків її мінорів, відмінних від нуля.

Безпосередньо з означення випливає, що:

1. Ранг існує для будь-якої матриці 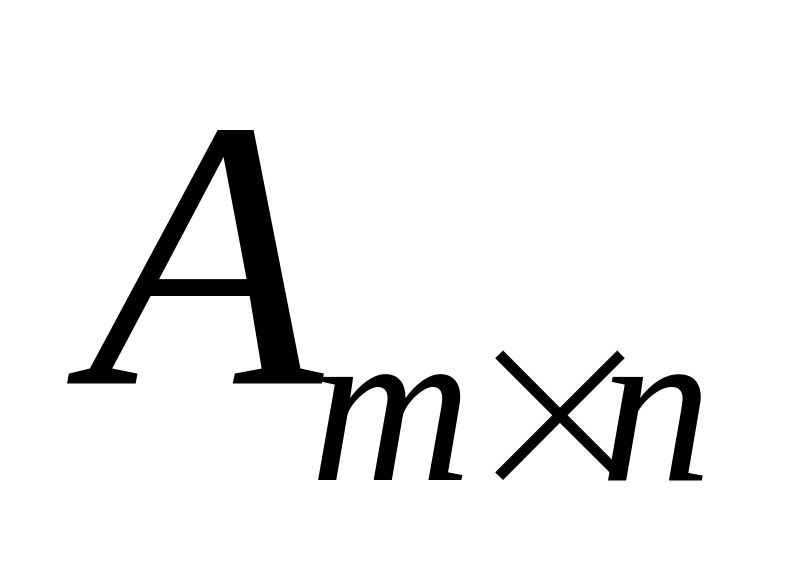, причому

2) тоді і тільки тоді, коли А = 0;

3) Для квадратної матриці п-го порядку ранг дорівнює п тоді і тільки тоді, коли матриця невироджена.

Правило знаходження рангу матриці:

1. Якщо всі мінори першого порядку (елементи матриці) дорівнюють нулю, то .

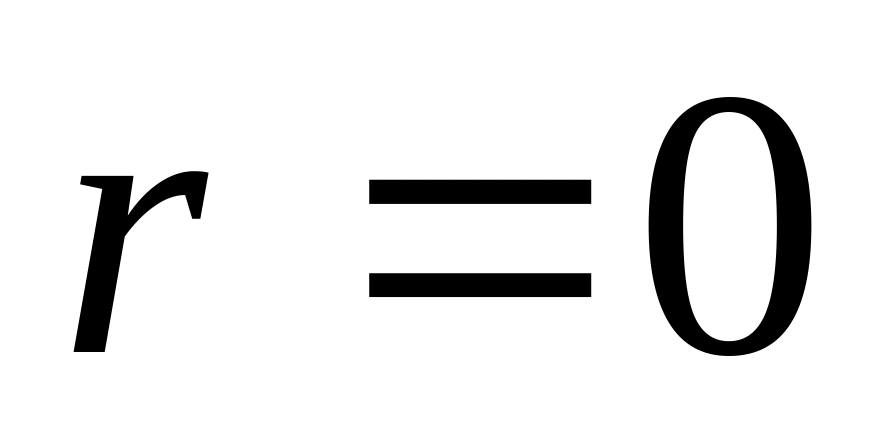2. Якщо хоч один з мінорів першого порядку відмінний від нуля, а всі мінори другого порядку дорівнюють нулю то .

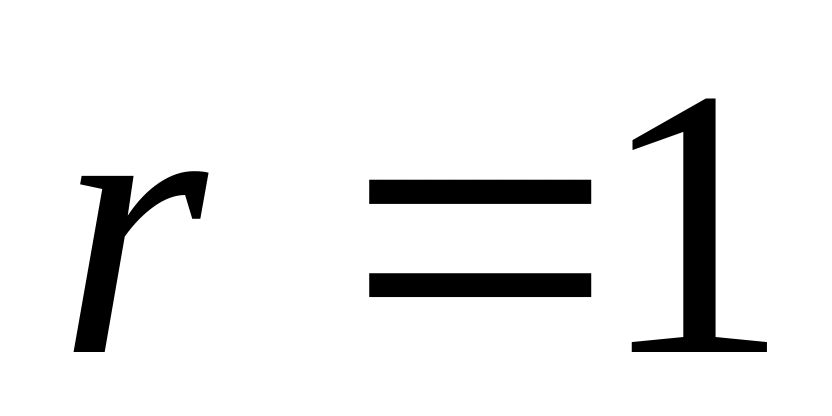3. У випадку, коли є мінор другого порядку, відмінний від нуля, досліджуємо мінори третього порядку. Так продовжуємо доти, поки не станеться одне з двох: або всі мінори порядку дорівнюють нулю, або мінорів порядку не існує, тоді .

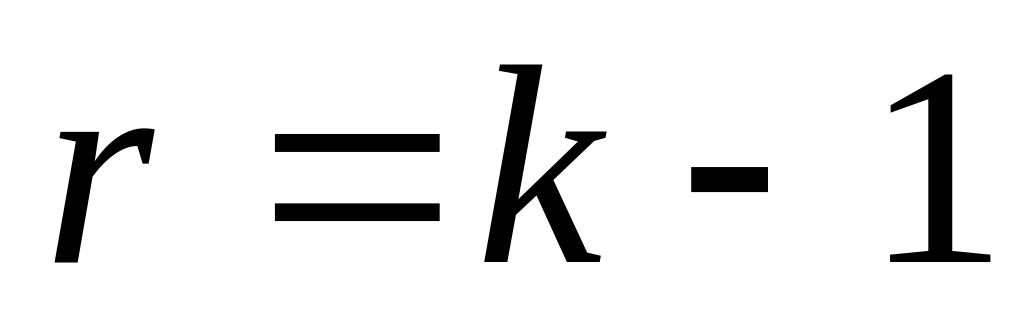Приклад 2.

Знайти ранг матриці

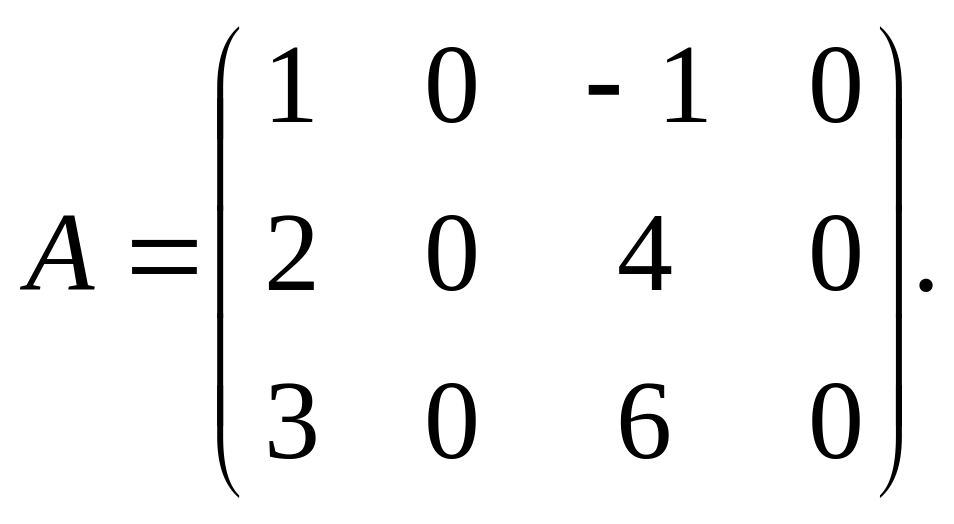
Серед мінорів першого порядку (тобто елементів матриці) є відмінні від нуля, тому

Оскільки один з мінорів другого порядку

а всі мінори третього порядку дорівнюють нулю, то

Вказаний метод знаходження рангу матриці не завжди зручний, тому що пов’язаний з обчисленням значного числа визначників.

Для обчислення рангу матриці застосовується також метод елементарних перетворень.

Елементарними перетвореннями матриці є:

а) перестановка місцями рядків (стовпців);

б) множення кожного елемента рядка (стовпця) на число, відмінне від нуля; в) додавання до елементів рядка (стовпця) відповідних елементів другого рядка (стовпця), помножених на одне і те саме число.

Приклад 3.

Знайти ранг матриці

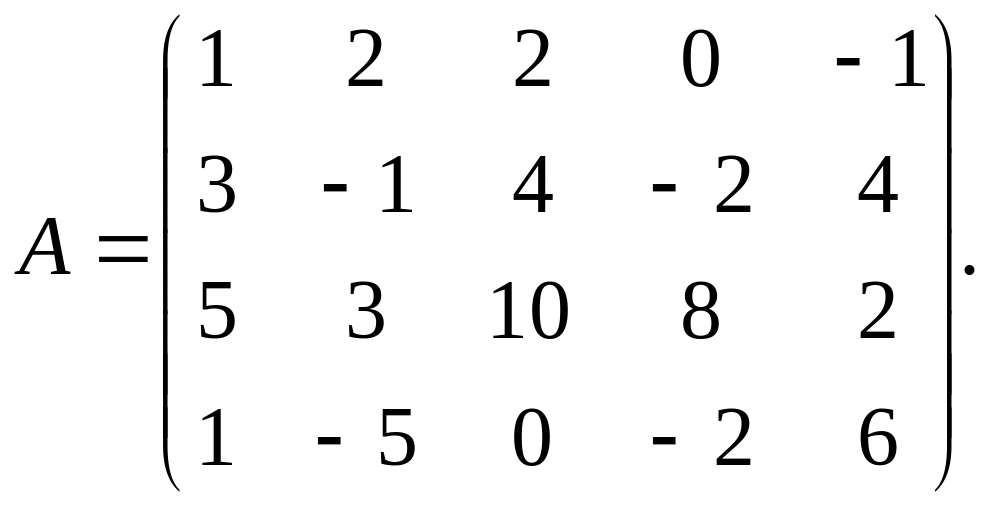
Виконуючи елементарні перетворення, маємо:

(Знак між матрицями показує, що вони утворюються одна з другою елементарними перетвореннями і, отже, мають один і той