
- •1.1 Предмет, цели и задачи методики преподавания математики и ее связи с другими науками.
- •1.2.Математика как учебный предмет в школе.
- •1.4 Воспитание учащихся в процессе обучения математике. Развитие познавательного интереса школьников при обучении математике.
- •1.5. Проблема интеграции школьного курса математики и пути её решения.
- •1.6 Дидактические принципы обучения школьников математике.
- •1.7 Развивающее обучение. Принципы развивающего обучения.
- •1.8 Общие дидактические методы обучения школьников математике. Классификация методов обучения.
- •1.9.Методы научного познания в обучении математике
- •1.11 Определение понятий. Классификация понятий. Возможные ошибки в определении математических понятий школьниками и работа учителя по их предупреждению.
- •1.12 Определение понятий. Виды определений. Требования к определениям. Методика изучения математических понятий в школе.
- •1.13. Математическое понятие: термин, объем, содержание. Классификация понятий. Требования к классификации. Способы образования математических понятий.
- •1.15 Структура теорем. Виды теорем. Методика изучения теорем в школьном курсе математики.
- •1.16 Сущность понятия «доказательства». Методы доказательства теорем.
- •1.17 Общие методы решения математических задач. Классификация задач. Роль алгоритмов и эвристик в обучении решению задач. Организация обучения решению математических задач.
- •1.18 Задачи в школьном курсе математики и общая методика их решения. Роль и функции задач в математике. Основные этапы в решении задачи. Общие умения по решению задач.
- •1.19 Современные формы организации обучения математике. Урок как основная форма организации учебного процесса. Типы уроков. Основные требования к современному уроку.
- •1.21 Воспитание у учащихся потребности в доказательствах теорем. Методика обучения учащихся теоремам и их доказательствам. Подготовка учителя к доказательству теорем на уроке.
- •1.22 Дифференциация в обучении школьников математике в системе основного и дополнительного образования.
- •1.23 Развитие математических способностей и воспитание учащихся в процессе математического образования.
- •1.24 Анализ урока математики. Его роль в интенсификации учебного процесса.
- •9. Выводы и предложения.
- •1.25 История развития методики преподавания математики. Основные противоречия процесса обучения математике. Актуальные проблемы методики преподавания математики.
- •2.1 Методика изучения начал систематического школьного курса планиметрии.
- •2.2 Методика изучения подобных треугольников.
- •2.3 Методика изучения основных соотношений между элементами треугольника.
- •2.4 Методика изучения понятия равенства фигур. Доказательство первых теорем планиметрии. Признаки равенства треугольников.
- •2.5 Методика изучения четырехугольников и их свойства.
- •2.6 Методика изучения величин в школьном курсе планиметрии.
- •2.13 Методика введения и изучения рациональных чисел.
- •2.13 Методика введения и изучения иррациональных чисел.
- •2.20 Методика изучения функций. Понятие функций. Возможная методическая схема изучения функций в базовой школе. Методика изучения алгебраических функций.
2.13 Методика введения и изучения иррациональных чисел.
Введение начинается с целесообразно подобранной задачи. Например: извлечение квадратного корня из положительного числа, не являющегося полным квадратом; каким числом выражается длина диагонали квадрата со стороной 1; чему равна сторона квадрата, если известно, что его площадь равна 3.
Практические задачи: задачи измерения; каждой ли точке координатной прямой соответствует рац число?
Изображение чисел на координатной прямой
Рис
Покажем, что т. В’ соответствует числу, не явл рацион, т. к. диагональ квадрата ОВ несоизмерима с его стороной ОА
Д-во, что т. В не соотв. никакому рац числу
Т. к. т. В’
находится на ОХ,
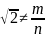
От противного:
пусть
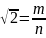 – несократимая дробь. Обе части –
неотрицательны, возведем в квадрат,
получим:
– несократимая дробь. Обе части –
неотрицательны, возведем в квадрат,
получим:
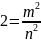 ,
,
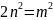 ,
=>
,
=> – четное, =>
– четное, =>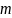 – четное. Значит
можно представить в виде
– четное. Значит
можно представить в виде
 .
Подставим в
:
.
Подставим в
:
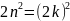 =>
=>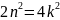 ,
,
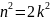 =>
=>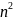 – четное,
– четное,
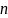 – четное. Тогда имеем
– четное. Тогда имеем
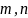 – четные. Это противоречит тому, что
– четные. Это противоречит тому, что
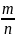 – несократимая дробь. =>
=>
– несократимая дробь. =>
=>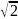 не
является рациональным числом.
не
является рациональным числом.
Таким образом, число можно изобразить на координатной прямой некоторым числом, которое не является рациональным. Такие числа называются иррациональными.
2 подход
Рис

С другой
стороны
 .
.
Если натуральное число не есть квадрат некоторого натурального числа, то оно есть квадрат иррационального числа. Таким образом, – иррациональное число.
3 подход
Иррациональные
числа – есть бесконечные десятичные
непериодические дроби. Так как
нельзя извлечь нацело
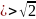 есть бесконечная десятичная непериодическая
дробь
есть число иррациональное.
есть бесконечная десятичная непериодическая
дробь
есть число иррациональное.
4 подход
Рассмотрим приближенное значение с недостатком и с избытком:
С недостатком: 1,4; 1,41; 1,414; 1,4142
С избытком: 1,5; 1,42; 1,415; 1,4143
Объединим эти последовательности: 1,4< 1,41< 1,414 <1,4142 < < 1,4143 < 1,415 < 1,42 < 1,5
Докажем, что границей или пределом последовательностей является некоторое иррациональное число.
Пусть границей явл , с другой стороны границей явл несократимая дробь .
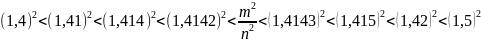
Таким образом,
на границе последовательности,
представляющей квадраты членов,
последовательности приближений с
недостатком и с избытком находится с
одной стороны число 2, а с другой -
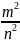 ,
причем
,
причем
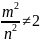 => данную последовательность определяют
два числа, не равные между собой, а это
невозможно => последовательности
определяют единственное число
.
=> данную последовательность определяют
два числа, не равные между собой, а это
невозможно => последовательности
определяют единственное число
.
Действия над иррациональными числами
1) сравнение (можно как десятичные дроби, сравнивая кол-во единиц в соответствующих разрядах, можно как квадраты корней)
2) сложение, вычитание, умножение, деление (нельзя выполнять как с десятичными дробями)
Часто иррациональные числа как бесконечные десятичные дроби заменяют их приближенными значениями, и результаты действий находят по правилам приближенных значений.
2.14 Методика изучения процентов. Основные задачи на проценты в школьном курсе математики.
Методика изучения тождественных преобразований.
2.16 Методика изучения тригонометрических уравнений и неравенств в средней школе.
2.17 Методика изучения показательных и логарифмических уравнений и неравенств в средней школе.
2.18 Методика изучения уравнений и их систем в средней школе. Равносильность уравнений. Алгебраические уравнения и их системы.
2.19 Методика изучения неравенств и их систем в средней школе. Метод интервалов при решении неравенств.
Изучение курса 9 класса начинается с обобщения и систематизации знаний о действительных числах: повторяются известные учащимся термины, рассматриваются отношения между числовыми множествами. Далее формулируются свойства числовых неравенств. Решение линейных неравенств с одной переменной сопровождается введением понятия равносильных уравнений и неравенств, формулировкой свойств равносильности уравнений и неравенств. Практические навыки получают развитие при решении систем линейных неравенств с одной переменной. Рассматривается также вопрос о доказательстве неравенств, учащиеся знакомятся с некоторыми приемами доказательства неравенств и применяют их в ходе решения несложных задач.
Пусть функции f (x) и g (x) заданы на некоторых числовых множествах X1 и X2. Неравенством с одной неизвестной называется отношение вида f (x) < g (x). (1)
(Вместо знака < могут стоять знаки >, ≤, ≥.)
Областью допустимых значений неравенства (ОДЗ) называется множество значений переменной, на котором обе части неравенства одновременно определены (имеют смысл). Таким образом,
![]() то есть пересечение множеств X1 и X2.
то есть пересечение множеств X1 и X2.
Число a называется решением неравенства (1), если при подстановке его вместо переменной x получаем верное числовое неравенство f (a) < g (a).
Понятно, что a, являясь решением неравенства (1), может лежать только в ОДЗ.
Поскольку проверить решение в неравенствах не так просто, как в уравнениях, искать решения лучше сразу в ОДЗ.
Решить неравенство − это означает найти все его решения или доказать, что их нет. Совокупность всех решений неравенства называется множеством решений неравенства.
Два неравенства,
f (x) <g (x) (2) и f1 (x) <g1 (x), (3)
называются равносильными на множестве X, если на этом множестве неравенства имеют одни и те же решения, то есть, если каждое решение неравенства (2) является решением неравенства (3), и наоборот, каждое решение второго неравенства является решением первого. Два неравенства, не имеющие решений на каком-либо множестве, также считаются равносильными на этом множестве.
Из приведённого определения следует, что если неравенство f1 (x) < g1 (x) окажется более простым, чем равносильное ему неравенство f (x) < g (x), то и решать нужно именно его, так как решения у него те же. Остаётся единственная проблема: как от неравенства (2) перейти к равносильному ему неравенству (3) или, как говорят, осуществить равносильный переход? Сформулируем несколько общих правил, позволяющих это делать.
Правило 1. Если функции f (x), g (x) и h (x) определены на множестве X, то неравенства f (x) > g (x) и f (x) + h (x) > g (x) + h (x)
равносильны на этом множестве.
Правило 2. Если h (x) > 0 на множестве X, то неравенства
![]()
равносильны на этом множестве.
Вывод. Обе части неравенства можно умножать на положительную функцию, не нарушая равносильности.
Правило 3. Если h (x) < 0 на множестве X, то неравенства
![]()
равносильны на этом множестве.
Вывод. Обе части неравенства можно умножать на отрицательную функцию, не нарушая равносильности, меняя при этом знак неравенства на противоположный.
Правило 4. Если f (x) ≥ 0, g (x) ≥ 0 на множестве X, то неравенства
![]()
равносильны на этом множестве.
Вывод. Если обе части неравенства f (x) > g (x) неотрицательны, то возведение в квадрат неравенства не нарушает равносильности. Заметим, что возводить неравенство в квадрат можно, только если обе части этого неравенства неотрицательны. Если хотя бы одна из частей неравенства отрицательна, возведение неравенства в квадрат, вообще говоря, не является равносильным преобразованием. Яснее всего это видно на примере числовых неравенств. Так, если верное неравенство −1 > −4 возвести в квадрат, то получится неверное неравенство 1 > 16. Такое противоречие вызвано именно тем, что части первоначального неравенства не были неотрицательными.
