Этапы построения уравнения регрессии
Решение задачи построения качественного уравнения регрессии, соответствующего эмпирическим данным и целям исследования, является достаточно сложным и многоступенчатым процессом. Его можно разбить на три этапа:
1) выбор формулы уравнения регрессии;
2) определение параметров выбранного уравнения;
3) анализ качества уравнения и проверка адекватности уравнения эмпирическим данным, совершенствование уравнения.
Выбор формулы связи переменных называется спецификацией уравнения регрессии. В случае парной регрессии выбор формулы обычно осуществляется по графическому отображению реальных статистических данных в виде точек в декартовой системе координат, которое называется корреляционным полем (диаграммой рассеивания).
|
|
|
Рис. 2. 2
На рисунке представлены три ситуации.
На графике
взаимосвязь между
и
близка к линейной, и прямая достаточно
хорошо соответствует эмпирическим
точкам. Поэтому в данном случае в качестве
зависимости между
и
целесообразно выбрать
.
На графике
реальная взаимосвязь между
и
,
скорее всего, описывается квадратичной
функцией
.
И какую бы мы не провели прямую, отклонения
точек наблюдений от нее будут существенными
и неслучайными.
На графике явная взаимосвязь между и отсутствует. Какую бы мы не выбрали форму связи, результаты ее спецификации и параметризации (определение коэффициентов уравнения0 будут неудачными.
В случае множественной регрессии определение подходящего вида зависимости является более сложной задачей.
Вопросы определения параметров уравнения (параметризации) и проверки качества (верификации) уравнения регрессии будут освещены ниже.
Регрессия по методу наименьших квадратов
Пусть имеется
набор значений двух переменных
и
.
Можно отобразить пары значений
,
,
точками на плоскости. Нашей задачей
является подобрать функцию
(в случае парной линейной регрессии
),
наилучшим образом описывающую зависимость
от
.
Подобрать функцию в данном случае
означает определить значения параметров
и
.
Как уже отмечалось, из-за влияния случайного фактора, мы не можем найти точные значения параметров по выборочным данным. Мы можем лишь их оценить. Обозначим оценку параметра через , оценку параметра через . Тогда оценка уравнения регрессии примет вид:
.
Существует ряд методов, позволяющих минимизировать отклонения линии регрессии от эмпирических данных. Однако метод наименьших квадратов (МНК) при выполнении определенных условий дает несмещенные и эффективные оценки параметров регрессии.
Суть МНК состоит
в минимизации суммы квадратов остатков:
.
Используя условия
минимума
получим систему нормальных уравнений:
Решив данную систему линейных алгебраических уравнений, получим
,
.
Интерпретация уравнения регрессии
Существуют два этапа интерпретации уравнения регрессии. Первый этап состоит в словесном истолковании уравнения так, чтобы это было понятно человеку, не являющемуся специалистом в области статистики. На втором этапе необходимо решить, следует ли ограничиться этим или провести более детальное исследование зависимости.
Оба этапа чрезвычайно важны. Второй этап мы рассмотрим несколько позже, а пока обратим основное внимание на первый этап. Это будет проиллюстрировано моделью регрессии для функции спроса, т. е. регрессией между расходами потребителя на питание ( ) и располагаемым личным доходом ( ) по данным для США за период с 1959 по 1983 г.
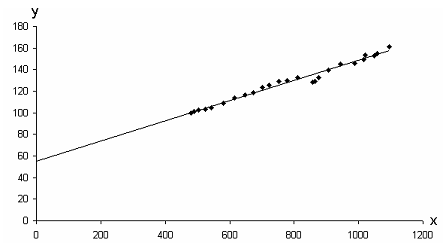
Предположим, что истинная модель описывается следующим выражением:
и оценена регрессия
Полученный результат можно истолковать следующим образом. Коэффициент при (коэффициент наклона) показывает, что если увеличивается на одну единицу, то возрастает на 0,093 единицы. Как , так и измеряются в миллиардов долларов в постоянных ценах; таким образом, коэффициент наклона показывает, что если доход увеличивается на 1 млрд. долл., то расходы на питание возрастают на 93 млн. долл. Другими словами, из каждого дополнительного доллара дохода 9,3 цента будут израсходованы на питание.
Что можно сказать
о постоянной в уравнении? Формально
говоря, она показывает прогнозируемый
уровень
,
когда
.
Иногда это имеет ясный смысл, иногда
нет. Если
находится достаточно далеко от выборочных
значений
,
то буквальная интерпретация может
привести к неверным результатам; даже
если линия регрессии довольно точно
описывает значения наблюдаемой выборки,
нет гарантии, что так же будет при
экстраполяции влево или вправо.
В рассматриваемом случае экстраполяция к вертикальной оси приводит к выводу о том, что если доход был бы равен нулю, то расходы на питание составили бы 55,3 млрд. долл. Такое толкование может быть правдоподобным в отношении отдельного человека, так как он может израсходовать на питание накопленные или одолженные средства. Однако оно не имеет никакого смысла применительно к совокупности. В данном случае константа выполняет единственную функцию: она позволяет определить положение линии регрессии на графике.
Представляет собой
интерес определить относительную
зависимость м от
,
т.е. узнать, на сколько процентов изменится
при изменении
на 1%. Такая величина называется
коэффициентом эластичности. По
определению, средний коэффициент
эластичности равен
В случае линейной
регрессии средний коэффициент эластичности
равен
.
При интерпретации уравнения регрессии чрезвычайно важно помнить о трех вещах.
Во-первых, является лишь оценкой , a — оценкой . Поэтому вся интерпретация в действительности представляет собой лишь оценку.
Во-вторых, уравнение регрессии отражает только общую тенденцию для выборки. При этом каждое отдельное наблюдение подвержено воздействию случайностей.
В-третьих, верность интерпретации зависит от правильности спецификации уравнения.