2. Обнаружение гетероскедастичности

Очень часто появление проблемы гетероскедастичности можно предвидеть заранее, основываясь на знании характера данных. В таких случаях можно предпринять соответствующие действия по устранению этого эффекта на этапе спецификации модели регрессии, и это позволит уменьшить или, возможно, устранить необходимость формальной проверки. К настоящему времени для такой проверки предложено большое число тестов (и, соответственно, критериев для них). Мы рассмотрим три обычно используемых теста (критерия), в которых делаются различные предположения о зависимости между дисперсией случайного члена и величиной объясняющей переменной (или объясняющих переменных): тест ранговой корреляции Спирмена, тест Голдфелда-Квандта и тест Уайта.

1. Тест ранговой корреляции Спирмена

При выполнении теста ранговой корреляции Спирмена предполагается, что дисперсия случайного члена будет либо увеличиваться, либо уменьшаться по мере увеличения , и поэтому в регрессии, оцениваемой с помощью МНК, абсолютные величины остатков и значения будут коррелированы. Данные по и остатки упорядочиваются, и коэффициент ранговой корреляции определяется как

,

(3)

где – разность между рангом и рангом .

Если предположить, что коэффициент корреляции для генеральной совокупности равен нулю, то коэффициент ранговой корреляции имеет нормальное распределение с математическим ожиданием 0 и дисперсией в больших выборках. Следовательно, соответствующая тестовая статистика равна и при использовании двустороннего критерия нулевая гипотеза об отсутствии гетероскедастичности будет отклонена при уровне значимости в 5%, если она превысит 1,96, и при уровне значимости в 1%, если она превысит 2,58. Если в модели регрессии имеется более одной объясняющей переменной, то проверка гипотезы может выполняться с использованием любой из них.

2. Тест Голдфелда—Квандта

Вероятно, наиболее популярным формальным критерием является критерий, предложенный С. Голдфелдом и Р. Квандтом (Goldfeld, Quandt, 1956). При проведении проверки по этому критерию предполагается, что стандартное отклонение ( ) распределения вероятностей пропорционально значению в этом наблюдении. Предполагается также, что случайный член распределен нормально и не подвержен автокорреляции.

Если графический анализ остатков указывает на возможную неоднородность дисперсий ошибок , то

1. наблюдения, насколько это возможно, упорядочивают в порядке предполагаемого возрастания дисперсий случайных ошибок;

2. отбрасывают центральных наблюдений (для более надежного разделения групп с малыми и большими дисперсиями случайных ошибок), так что для дальнейшего анализа остается наблюдений;

3. производят оценивание выбранной модели отдельно по первым 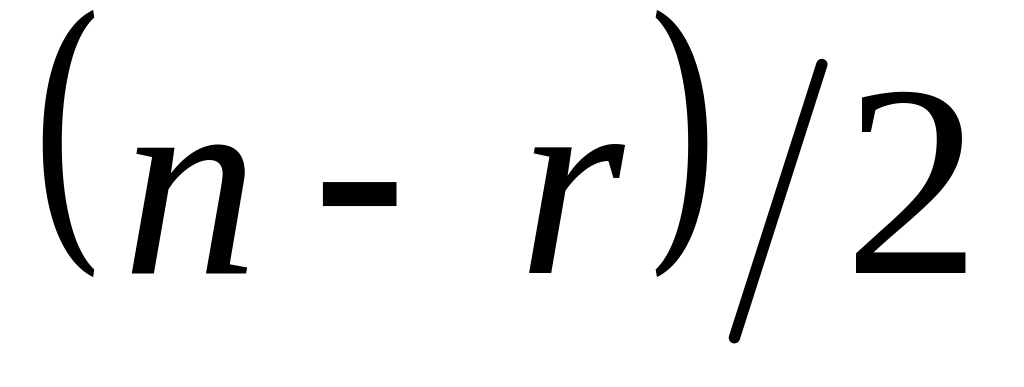и по последним наблюдениям;

4. вычисляют отношение 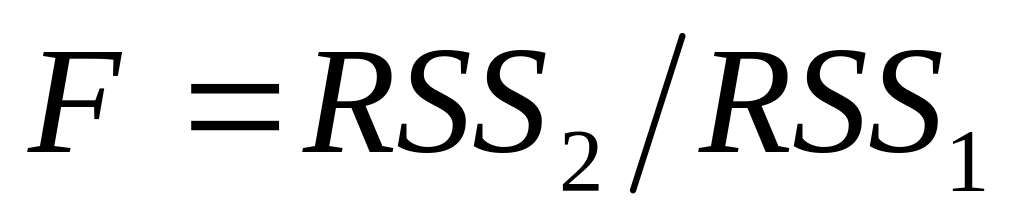остаточных сумм квадратов, полученных при подборе модели по последним (остаточная сумма квадратов ) и по первым (остаточная сумма квадратов ) наблюдениям.

При принятии решения учитывают, что если все же , (дисперсии однородны) и выполнены остальные стандартные предположения о модели наблюдений, включая предположение о нормальности ошибок, то тогда отношение имеет -распределение Фишера с и степенями свободы.

Гипотеза , (дисперсии однородны) отвергается, если вычисленное значение -отношения «слишком велико», т. е. превышает критический уровень соответствующий выбранному уровню значимости .