4.3 Решение матричной игры сведением к задаче линейного программирования в среде Excel

-3	1
0	1
-1	1
1	1

	7	3	7	3
	7	3		3

Среди элементов матрицы есть отрицательные

.

Введем переменные для игрока , для игрока .

ПЗЛП для игрока 1:

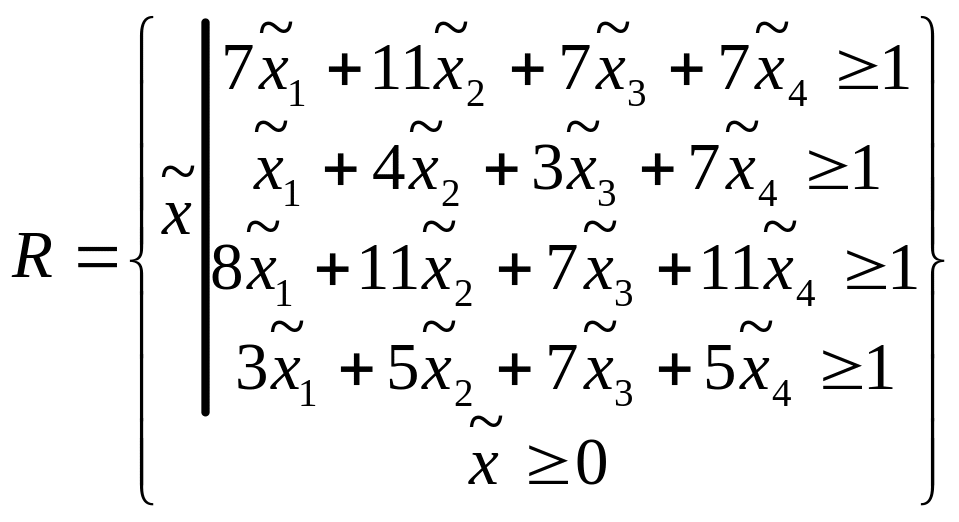
ДЗЛП для игрока 2:

Таблица 4.1 - Решение ПЗЛП в среде Excel

0,176471		1,235294
	0	1
	1,31E-17	1,705882
	0,058824	1
	0,117647	0
		1,31E-17
		0,058824
		0,117647

Таблица 4.2 – Решение ДЗЛП в среде Excel 0,176471 1,54E-33 0,411765 0,058824 0,823529 0 1 0,117647 1 1,54E-33 0,058824 0 0,117647

Переход к решению исходной игры.

Проверка:

Ответ:

Модель поведения потребителя

5.1 Задание

Найти максимум функции полезности , при заданных ценах и доходе потребителя

,

где - параметры варианта:

- количество букв в

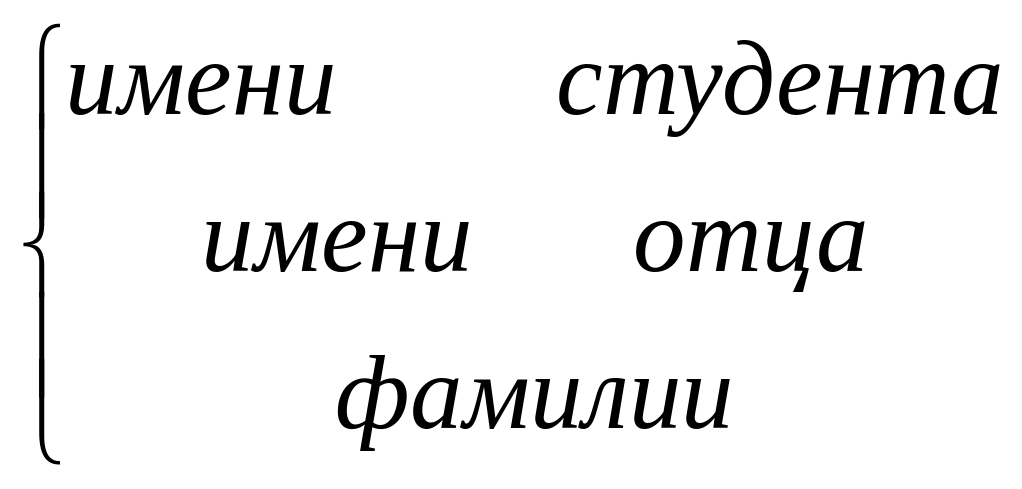
5.2 Алгоритм решения

1. Составить функцию Лагранжа

2. Для нахождения локального максимума функции Лагранжа вычислить необходимые условия

3. Решить систему уравнений п.2, найти 2 оптимальное решение .

4. Вычислить оптимальное значение функции полезности .

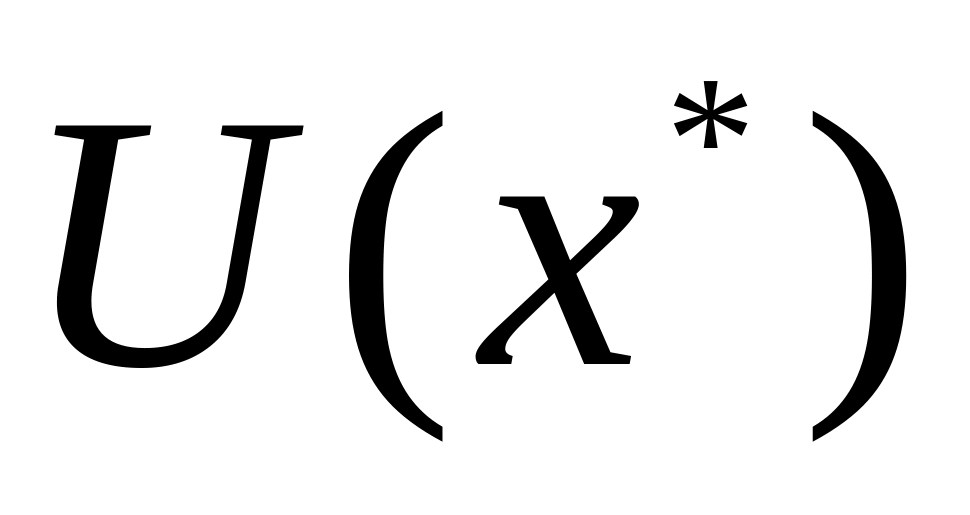5.3 Пример решения модели

Задание:

1.

2.

3.

Поделим первое уравнение на второе, второе – на третье, получим:

.

Найдем , подставив в первое уравнение системы

;

4.

Проверка:

Ответ: