3.3 Сепарабельное программирование

В качестве приближения к нелинейной функции на большом отрезке используется её кусочно-линейная аппроксимация, если разбить отрезок на подинтервалы и построить линейные приближения функции на каждом из подинтервалов. Этот метод применим только к сепарабельным функциям.

 Определение.

Функция  , где  - N-мерный вектор, называется сепарабельной, если она представляется в виде суммы функций, каждая из которых зависит только от одной из N переменных, т.е.

            

Кусочно-линейная аппроксимация для сепарабельной непрерывной функции f(x) строится следующим образом. Интервал значений каждой переменной x_i разбивается при помощи сетки с K_i узлами. Таким образом, на интервале x_i^(L) Ј x_i Ј x_i^(R) рассматривается следующая последовательность точек:

            x_i^(L) = x_i⁽¹⁾ < x_i⁽¹⁾ <...< x_i^(K_i⁾ = x_i^(R)

Введём обозначение f_i^(k) = f_i(x_i^(k)). Тогда аппроксимирующая функция примет вид:

            

причём при всех i=1,...,N выполняется:

            

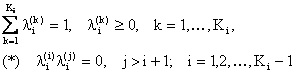
Последнее условие выражает тот факт, что не более двух переменных l⁽ⁱ⁾ должны быть положительными.

Таким образом, нелинейная функция f(x) заменяется кусочно-линейной  . Для построения хорошего приближения число узлов сетки должно быть большим, то есть линейность достигается за счёт роста размерности задачи, то есть решение задачи НЛП сводится к решению задачи ЛП большой размерности с переменными l_i^(k). Полученная задача ЛП может быть решена с помощью симплекс-метода, дополненного правилом ограниченного ввода в базис, учитывающего условие (*).

Решение, полученное с помощью сепарабельного программирования, представляет собой локальный минимум. Сходимость к глобальному минимуму гарантирована только тогда, когда целевая функция и допустимая область выпуклы. Метод сепарабельного программирования подходит для решения задач, которые в основном линейный, а отклонения от линейности представляются сепарабельными функциями. Если не требуется высокой точности, то приближенное решение задачи можно получить в процессе однократного решения задачи ЛП.

Мы рассмотрели два подхода к решению нелинейных задач. Первый (метод непосредственной линеаризации) эффективен в окрестности базовой точки и ненадёжен при удалении от неё. Второй (сепарабельное программирование) даёт хорошие приближения во всей области определения каждого ограничения, однако он применим только к сепарабельным задачам и его точность сильно зависит от густоты узлов сетки. Поэтому, необходимо построить алгоритм, использующий довольно грубые аппроксимации внешних частей ограничений для достижения окрестности оптимальной точки и строящий более тонкие аппроксимации в этой окрестности.

3.4 Выпуклое программирование

Определение 1    Задачей выпуклого программирования называется задача нелинейного программирования, у которой все функции являются выпуклыми функциями. Таким образом, задача выпуклого программирования является задачей минимизации выпуклой функции на выпуклом множестве, образованном системой выпуклых неравенств.

Основные свойства выпуклых и вогнутых функций:

1. Множество точек минимума выпуклой функции, заданной на выпуклом множестве ‑ выпукло.

2. Пусть f(x) ‑ выпуклая функция, заданная на замкнутом выпуклом множестве  . Тогда локальный минимум  f(x) на Х является и глобальным.

3. Если глобальный минимум достигается в двух различных точках, то он достигается и в любой точке отрезка, соединяющего данные точки.

4. Если  f(x)‑ строго выпуклая функция, то ее глобальный минимум на выпуклом множестве Х достигается в единственной точке.

5. Пусть функция f(x) ‑ выпуклая функция, заданная на выпуклом множестве Х, и, кроме того, она непрерывна вместе со своими частными производными первого порядка во всех внутренних точках Х. Пусть   – точка, в которой  . Тогда в точке  достигается локальный минимум, совпадающий с глобальным минимумом.

6. Множество точек глобальных (следовательно, и локальных) минимумов выпуклой функции f(x), заданной на ограниченном замкнутом выпуклом множестве Х, включает хотя бы одну крайнюю точку; если множество локальных минимумов включает в себя хотя бы одну внутреннюю точку множества Х, то  f(x) является функцией-константой.

Рассмотрим задачу нелинейного программирования

                                      (1)  

     (2)

             (3)                                     

Для  решения  сформулированной  задачи  в  такой  общей  постановке  не  существует  универсальных методов. Однако для отдельных классов задач, в которых сделаны дополнительные ограничения относительно свойств функций , разработаны эффективные методы их решения.

Множество допустимых решений задачи (1) – (3) удовлетворяет условию регулярности, или условию Слейтера, если существует по крайней мере одна точка  , принадлежащая области допустимых решений такая, что 

Задача (1) – (3)  называется задачей выпуклого программирования, если функция  является выпуклой, а функции  – выпуклыми. Функцией Лагранжа задачи выпуклого программирования (1) – (3)  называется функция

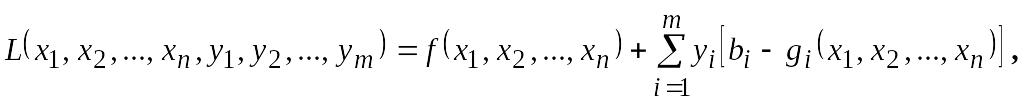
       где  – множители Лагранжа.

Точка  называется седловой точкой функции Лагранжа, если

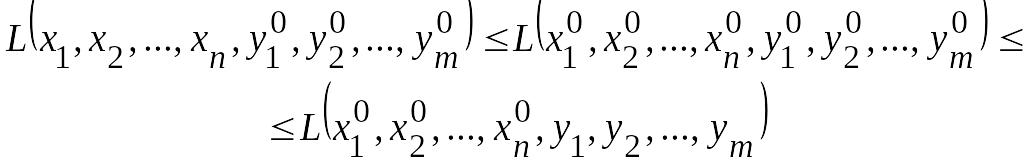
       для всех  и .

Теорема (Куна – Таккера).  Для   задачи   выпуклого   программирования   (1) – (3),   множество   допустимых   решений   которой   обладает свойством  регулярности,    является  оптимальным  решением  тогда  и только тогда, когда существует такой вектор   , что  – седловая точка функции Лагранжа.

Если предположить, что функции  и  непрерывно дифференцируемы, то теорема Куна – Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка  была седловой точкой функции Лагранжа, т. е. являлась решением задачи выпуклого программирования:

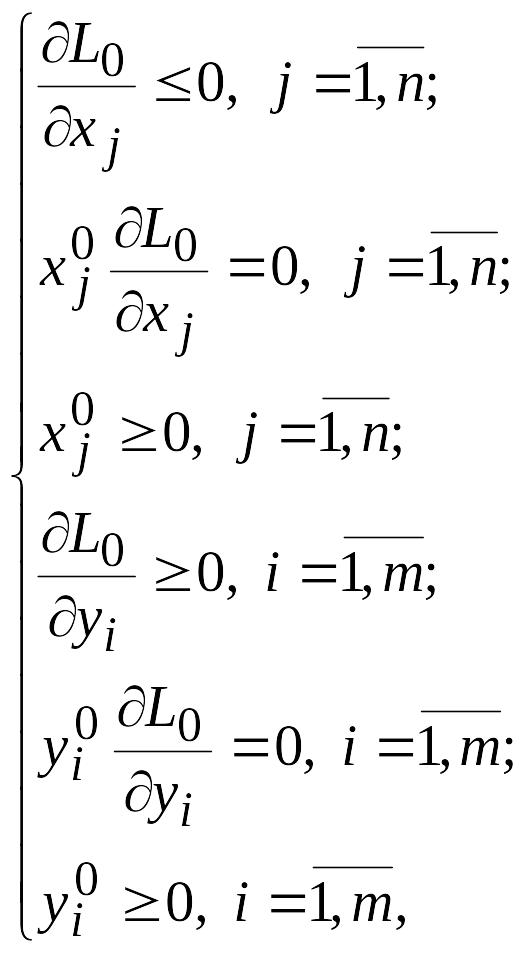
где  и  – значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке.