- •Введение
- •Тема 1 Математическое программирование и оптимизация
- •1.1 Эволюция развития математических методов и моделей в экономике
- •1.2 Классификация экономико-математических моделей
- •1.3 Математическое программирование
- •1.4 Оптимизация в математике и ее методы
- •1.5 Метод Монте-Карло
- •1.5.1 Алгоритм Бюффона для определения числа Пи
- •1.5.2 Связь стохастических процессов и дифференциальных уравнений
- •1.5.3 Рождение метода Монте-Карло в Лос-Аламосе
- •1.5.4 Дальнейшее развитие и современность
- •1.5.5 Интегрирование методом Монте-Карло
- •1.5.6 Обычный алгоритм Монте-Карло интегрирования
- •1.5.7 Геометрический алгоритм Монте-Карло интегрирования
- •Тема 2 Линейное программирование
- •2.1 Общая задача линейного программирования
- •2.2 Основная задача лп (озлп)
- •2.3 Симплекс-метод линейного программирования
- •2.4 Двойственные задачи линейного программирования
- •2.5 Целочисленное линейное программирование
- •2.6 Параметрическое линейное программирование
- •2.7 Дробно-линейное программирование
- •2.8 Блочное программирование
- •2.9 Теория графов
- •2.10 Транспортная задача
- •2.10.1 Общая характеристика транспортной задачи
- •2.10.2 Математическая модель транспортной задачи
- •Тема 3 Нелинейное программирование
- •3.1 Методы нелинейного программирования
- •3.2 Метод множителей Лагранжа
- •3.3 Сепарабельное программирование
- •3.4 Выпуклое программирование
- •3.5 Квадратичное программирование
- •3.6 Геометрическое программирование
- •3.7 Динамическое программирование
- •3.8 Стохастическое программирование
- •Тема 4 Межотраслевой баланс и сетевое моделирование
- •4.1 Задача межотраслевого баланса
- •4.2 Балансовая модель Леонтьева
- •4.3 Модели межотраслевого баланса в планировании инновационных программ
- •4.3.1 Однопродуктовая динамическая макроэкономическая модель
- •1) Открытая однопродуктовая динамическая модель Леонтьева
- •2) Замкнутая однопродуктовая модель Леонтьева
- •4.4 Сетевая модель данных
- •4.4.1 Историческая справка
- •4.4.2 Основные элементы сетевой модели данных
- •4.4.3 Особенности построения сетевой модели данных
- •4.4.4 Операции над данными сетевой модели
- •4.4.5 Использование сетевой модели
- •4.5 Сетевой график
- •4.6 Методика составления сетевого графика
- •5. Задачи оптимального проектирования
- •5.1. Постановка задачи оптимального проектирования
- •5.1.1. Основные понятия и определения
- •5.2. Пример задачи оптимального проектирования
- •5.3. Классификация задач оптимального проектирования
- •Первая постановка
- •5.4 Определение уравнений линейной регрессии
- •5.7. Методика получения исходных данных
- •5.3. Решение задач оптимального проектирования
- •5.3.1. Оптимизация параметров изделия
2.4 Двойственные задачи линейного программирования
Каждой задаче линейного программирования можно поставить в соответствие задачу, называемую двойственной к исходной.
Предположим, что в производстве используется m различных видов ресурсов, объем которых ограничен величинами b1, b2,.., bm. И производится n различных видов продукции, величина выпуска которых определяется переменными х1, х2,…, хn. Известны нормы затрат каждого ресурса на единицу каждого вида продукции, образующие матрицу
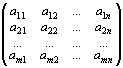 .
.
Известна также стоимостная оценка (цена) единицы продукции каждого вида с1, с2,…, сn.
Задача сводится к следующему: найти такие значения переменных х1, х2,…, хn, при которых расход ресурсов не превышает заданного их количества, а стоимость всей продукции достигает максимума.
В математической форме задача записывается следующим образом: максимизировать
L = c1x1+c2x2+…+cnxn (2.7)
при
условиях 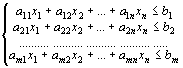 (2.8)
(2.8)
![]() 0 (j=1,
2,.., n).
0 (j=1,
2,.., n).
На базе тех же исходных данных может быть поставлена еще одна задача, в которой переменными величинами являются оценки у1,у2,…,уm, приписываемые каждому виду ресурсов. Они должны быть такими, чтобы общая оценка всего имеющегося количества ресурсов была минимальной, но при условии, что суммарная оценка ресурсов, расходуемых
на единицу любого вида продукции, будет не меньше, чем цена за эту единицу.
Математическая задача записывается следующим образом: минимизировать
L = b1y1+b2y2+…+bmym (2.9)
при
условиях 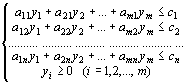 (2.10)
(2.10)
Задачи (2.7) – (2.8) и (2.9) – (2.10) образуют пару взаимодвойственных задач, и любая из них может рассматриваться как исходная.
Сосредотачивая внимание на экономическом содержании и размерности постоянных переменных величин рассматриваемых задач, можно записать следующие соотношения:
для прямой (исходной) задачи максимизируемая функция
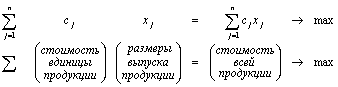
ограничивающие условия
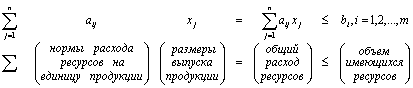 ;
;
для двойственной задачи минимизируемая функция
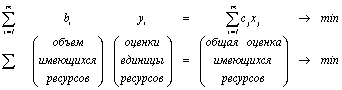
ограничивающие условия
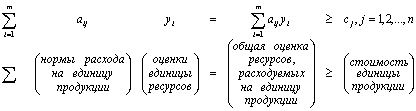 .
.
Эти задачи обладают следующими свойствами:
1. В одной задаче ищется максимум целевой функции, в другой – минимум.
2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи, и наоборот.
3. В каждой задаче система ограничений задается в виде неравенств, причем в задаче, в которой ищется максимум целевой функции, все неравенства вида «», а в задаче, в которой находится минимум целевой функции, все неравенства вида «».
4. Коэффициенты при переменных системах ограничений записываются матрицами
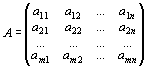
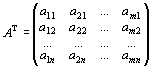 ,
,
транспонированными относительно друг друга.
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6. Условия неотрицательности переменных сохраняются в обоих задачах.
Пример. Исходная задача
L = 10x1+6x2-4x3min
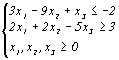
Приводим все неравенства системы ограничений исходной задачи к одному знаку:
L = 10x1+6x2-4x3min
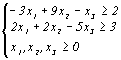
Двойственная задача
L = 2y1+3y2max
при
условиях