§ 7. Схема Бернулли
Пусть производится серия из испытаний, в каждом из которых событие может наступить, а может и не наступить. Пусть при этом выполнено следующее условие: вероятность наступления события в каждом испытании постоянна, т.е. не зависит ни от номера испытания, ни от результатов предыдущих испытаний.
Последовательность испытаний, удовлетворяющую указанному условию, называют последовательностью независимых испытаний или схемой Бернулли. Схема Бернулли полностью определяется двумя числами: количеством испытаний и вероятностью появления события в одном испытании – .
Теорема. Вероятность того, что в последовательности из испытаний в схеме Бернулли событие наступит ровно раз выражается формулой:
,
(
). (1)
Доказательство.
Вероятность одного сложного события,
состоящего в том, что в
испытаниях событие
наступит
раз равно
(по теореме умножения независимых
событий). Таких сложных событий может
быть столько, сколько можно составить
сочетаний из
элементов по
,
т.е.
.
Все они несовместны. По теореме сложения
имеем:
раз
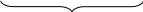
Полученную формулу называют формулой Бернулли.
Пример 1.
Найти вероятность того, что при 10-кратном бросании монеты выпадет ровно 3 герба.
Решение.
,
,
,
.
.
Пример 2.
Найти вероятность того, что при 10-кратном
бросании монеты количество гербов
окажется в пределах
.
Решение.
Очевидно, что при больших значениях в схеме Бернулли использовать формулу (1) весьма затруднительно (сложно вычислить ). Обычно в этих случаях используют следующие теоремы:
Теорема (локальная теорема Муавра-Лапласа).
При больших значениях в схеме Бернулли справедливо приближенное равенство:
,
где
,
.
Теорема (интегральная теорема Муавра-Лапласа).
При больших значениях в схеме Бернулли имеет место приближенное равенство:
,
где
,
,
.
Раздел II случайные величины § 1. Понятие случайной величины. Дискретные и непрерывные случайные величины. Интегральная и дифференциальная функции распределения
Понятие случайной величины является одним из основных понятий теории вероятности.
Определение. Случайной величиной называется величина, которая в результате испытания принимает то или иное значение. При этом заранее неизвестно, какое именно значение случайная величина примет в результате опыта.
Изучая случайную величину, прежде всего
интересуются множеством ее возможных
значений. Это может быть конечное
множество чисел или множество чисел,
не имеющее предельной точки (например,
множество
)
Такие случайные величины называются
дискретными.
Возможно, что множество значений случайной величины содержит целый отрезок числовой оси. Такие случайные величины называются непрерывными.
Пример 1.
Случайная величина
– количество очков, выпавшее при бросании
игральной кости.
– множество значений.
Пример 2.
Случайная величина – угол между начальным направлением и направлением остановившейся стрелки рулетки.
– множество значений.
Определение. Распределением
(законом распределения) дискретной
случайной величины называется функция,
сопоставляющая каждому возможному
значению
случайной величины ее вероятность
(
),
причем
.
Распределение дискретной случайной величины с конечным числом возможных значений удобно задавать таблицей.
Пример 3.
Закон распределения из примера 1 имеет вид:
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
1 |
Закон распределения полностью характеризует дискретную случайную величину, указывая возможные значения и вероятности, с которыми эти значения появляются в результате испытаний.
Перейдем к обсуждению понятия распределения непрерывной случайной величины. Рассматривают два вида распределений непрерывной случайной величины: интегральное и дифференциальное, их также называют интегральной и дифференциальной функциями распределения, интегральным и дифференциальным законами распределения.
Определение. Интегральной функцией
распределения непрерывной случайной
величины
называется функция переменной
,
выражающая вероятность того, что
случайная величина
в результате испытания примет значение,
меньшее, чем число
,
т.е.
.
Свойство 1. 
.
Доказательство следует из определения интегральной функции распределения как вероятности.
Свойство 2.
– неубывающая функция, т.е. из
.
Доказательство.
Событие
можно подразделить на два несовместных
события
и
.
По теореме сложения вероятностей имеем:
.
Отсюда
. (1)
В
ероятность
любого события неотрицательна,
следовательно
.
Свойство 3. 
.
Доказательство.
В формуле (1) при
,
имеем
.
Следствие. Вероятность того, что непрерывная случайная величина примет определенное значение, равна 0.
Доказательство.
.
Пусть
.
Т.к.
– непрерывная случайная величина, то
функция
– непрерывна. Отсюда
.
Замечание 1. Из доказанного следствия имеем
.
Замечание 2. Было бы неправильно
думать, что
означает, что событие
невозможно.
Свойство 4. Если возможные
значения случайной величины принадлежит
интервалу
,
то:
1) 
при
;
2) 
при
.
Доказательство.
Пусть
,
тогда событие
– невозможно и
.
Пусть
,
тогда событие
– достоверно и
.
Следствие. Если возможные
значения непрерывной случайной величины
расположены на всей числовой оси
,
то справедливы следующие предельные
соотношения:
и
.
Определение. Пусть – непрерывная случайная величина и – ее интегральная функция распределения. Пусть, кроме того – дифференцируема всюду, за исключением, быть может, конечного числа точек.
Производная
интегральной функции распределения
называется дифференциальной функцией
(дифференциальным законом) распределения
непрерывной случайной величины
.
Свойство 1. Дифференциальная функция распределения – неотрицательная функция:
.
Доказательство.
Интегральная
функция распределения
– неубывающая, следовательно,
.
Свойство 2. 
.
Свойство 3. 
.
Доказательство.
.
Следствие. 
Замечание 1. Значения функции
называют обычно плотностью вероятности
случайной величины
.
Такое название объясняется следующими
обстоятельствами:
.
есть “средняя вероятность”, т.е.
вероятность
,
отнесенная к единице длины.
Замечание 2. Понятие интегральной функции распределения имеет место и для дискретных случайных величин. График этой функции в таком случае имеет ступенчатый вид.
Для описания дискретной случайной величины понятие дифференциальной функции распределения неприменимо.