IV. Интегралы вида

,

где – вещественные числа.

Из тригонометрии известно, что произведения тригонометрических функций, находящихся под знаком этих интегралов, преобразуются в суммы по следующим формулам:

;

;

.

Заменив в рассматрива6емых интегралах подынтегральные функции по этим формулам, легко выполним интегрирование.

Задача V.IV.1. Найти интегралы: 1) ; 2) ; 3) ;

4) .

1) ▲

. ▼

2) ▲

. ▼

3) ▲

. ▼

4) ▲

. ▼

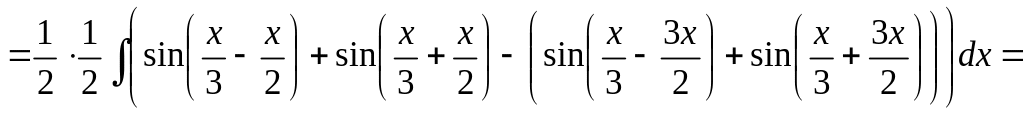
V. Интегралы вида

.

Запись означает, что над синусом и косинусом производятся только рациональные операции: сложение и вычитание, умножение на постоянные величины, возведение в целые степени как положительные, так и отрицательные, деление. Другими словами, под символом следует понимать рациональную функцию синуса и косинуса.

Интегралы указанного вида приводятся к интегралам от рациональных функций с помощью, так называемой универсальной тригонометрической подстановки

.

В результате этой подстановки имеем:

;

.

Задача V.V.1. Найти интегралы: 1) ; 2) ; 3) ; 4) .

1) ▲

. ▼

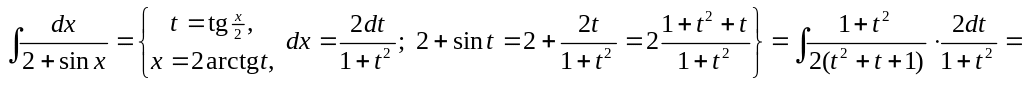
2) ▲

. ▼

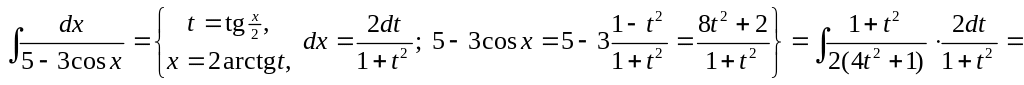
3) ▲

. ▼

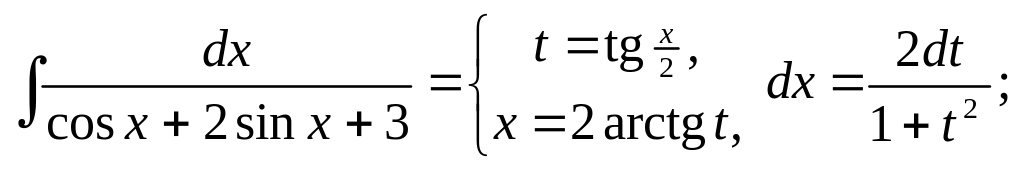
4) ▲

. ▼

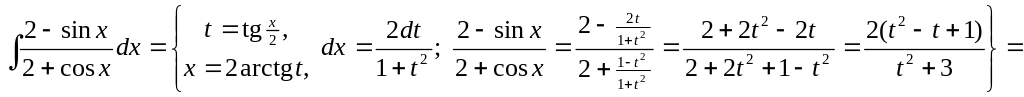
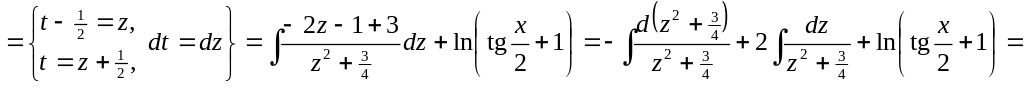
Универсальная подстановка приводит во многих случаях к сложным вычислениям, так как при ее применении выражаются через переменную в виде рациональных дробей, содержащих .

В ряде случаев рационализация подынтегрального выражения может быть достигнута с помощью других, более простых подстановок. Приведем важнейшие из этих случаев.

1. Если подынтегральная функция имеет вид

,

где – рациональная функция одного аргумента, то применяется подстановка

.

Замечание. Если функция меняет знак при замене ,

т. е. является нечетной функцией , то применяется подстановка .

2. Если подынтегральная функция имеет вид

,

где – рациональная функция одного аргумента, то применяется подстановка

.

Замечание. Если функция меняет знак при замене ,

т. е. является нечетной функцией , то применяется подстановка .

3. Если функция не изменяется при замене на и

на , т. е. ,

то для нахождения интеграла целесообразно использовать подстановку .

Задача V.V.2. Найти интегралы: 1) ; 2) ; 3) .

1) ▲

. ▼

2) ▲

. ▼

3) ▲

. ▼

Решение задач 22-24, 26 типового варианта

Найти неопределенные интегралы.

1. ▲

. ▼

2. ▲

. ▼

3. ▲

. ▼

4. ▲

. ▼

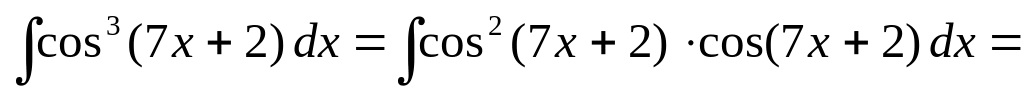
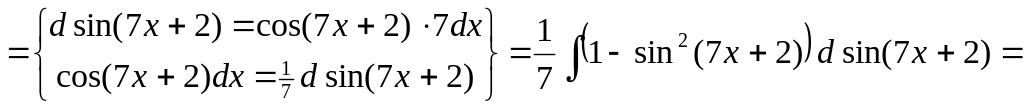
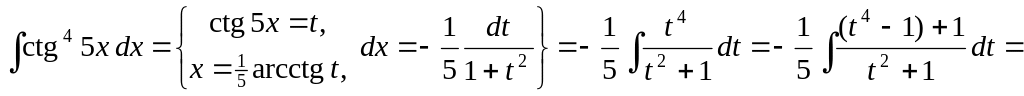
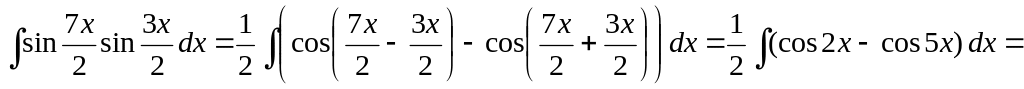
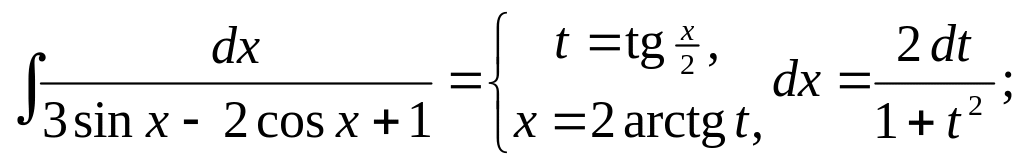
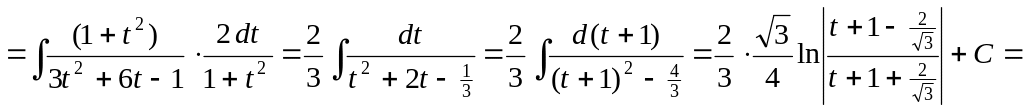
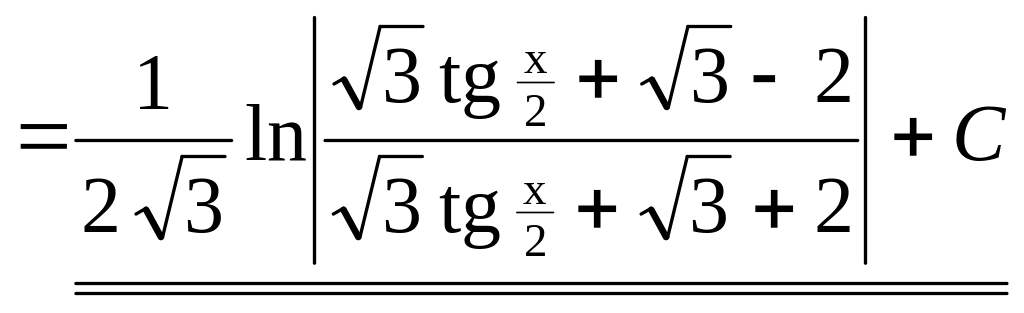VI. Интегрирование некоторых иррациональных функций

В отличие от функций рациональных иррациональные выражения далеко не всегда интегрируются в элементарных функциях. Рассмотрим некоторые частные типы иррациональных функций, интегрирующихся в конечном виде.

а) Интегралы вида

.

Вычисление интеграла производится так:

1. под корнем следует вынести за скобку

,

– за знак интеграла;

2. после этого под корнем выделить полный квадрат

;

3) применить формулу или .

(Если , то вынесение за скобку становится излишним, и надо только выделить под корнем полный квадрат).

Задача 1. Найти интегралы: 1) ; 2) .

1. ▲

. ▼

2. ▲

. ▼

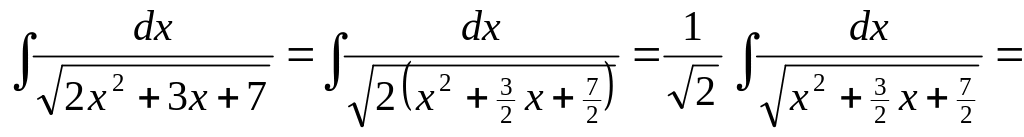
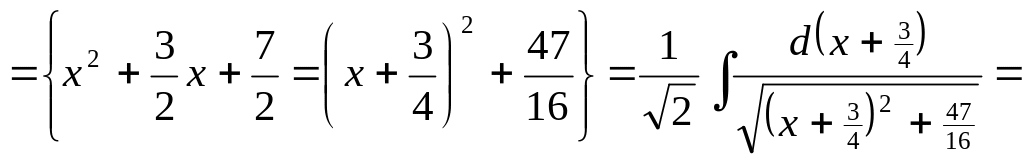
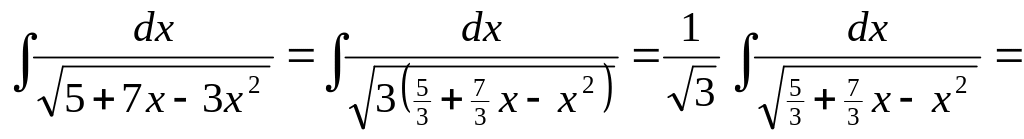
б) Интегралы вида

.

Вычисление интеграла производится так:

1. под корнем следует вынести за скобку

,

– за знак интеграла;

2) после этого под корнем выделить полный квадрат

;

3) ввести новую переменную ;

4) применить формулу или .

(Если , то вынесение за скобку становится излишним, и надо только выделить под корнем полный квадрат).

Задача 2. Найти интегралы: 1) ; 2) .

1. ▲

. ▼

2. ▲

. ▼
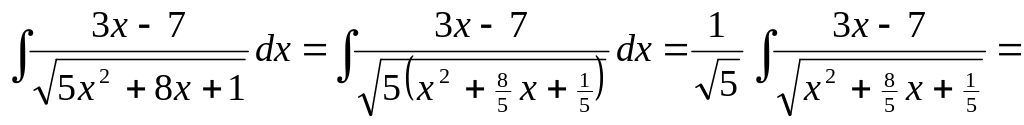
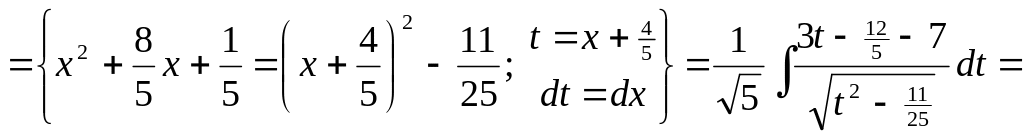
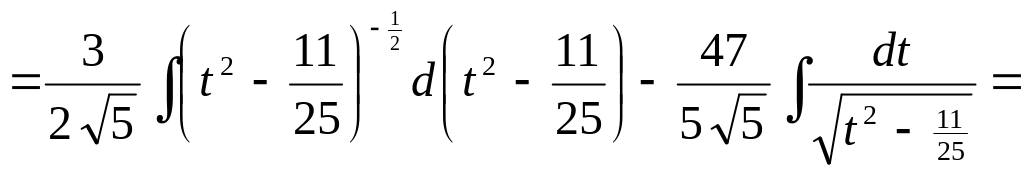
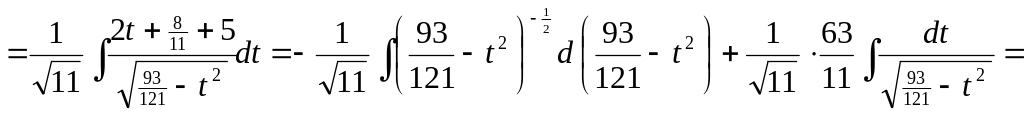