Некоторые корни знаменателя – комплексные числа

Задача IV.3. Разложить на простейшие дроби рациональную дробь .

▲ Данная дробь правильная .

Разложим знаменатель на множители: .

Квадратичный множитель вещественных корней не имеет, а потому имеет место разложение

.

Умножая обе части равенства , получаем

Для определения неизвестных коэффициентов применим комбинированный метод

Искомое разложение имеет вид

.

Корни знаменателя – кратные комплексные числа

Задача IV.4. Разложить на простейшие дроби рациональную дробь .

▲ Данная дробь правильная .

1. Знаменатель уже разложен на множители и не имеет вещественных корней.

2. Поэтому разложение на простейшие дроби должно иметь вид

.

3. Умножая обе части равенства 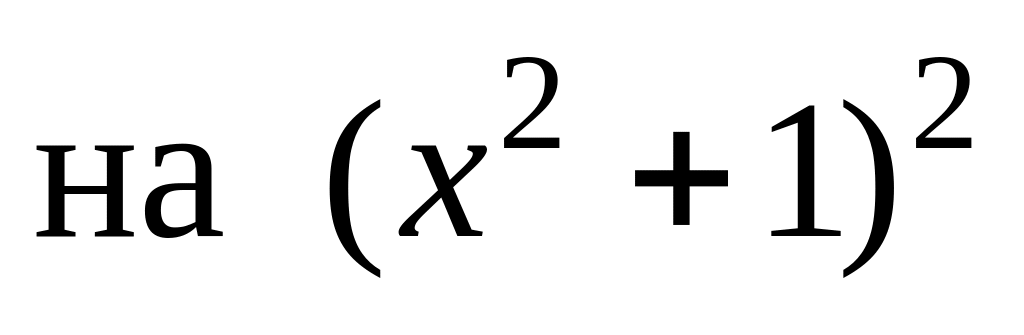, получаем

или .

4. Для определения неизвестных коэффициентов 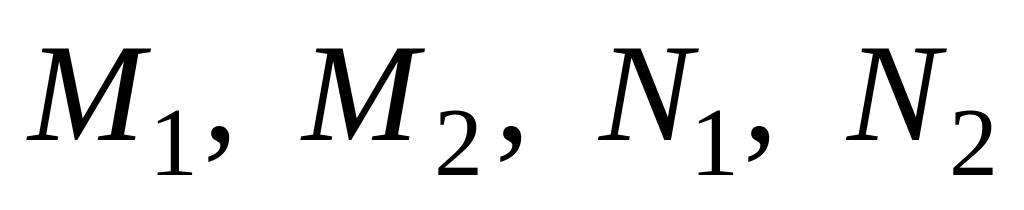применим метод неопределенных коэффициентов. Приравнивая коэффициенты при одинаковых степенях в левой и правой частях последнего равенства, будем иметь

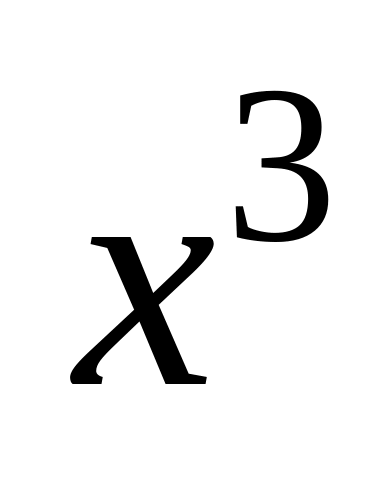
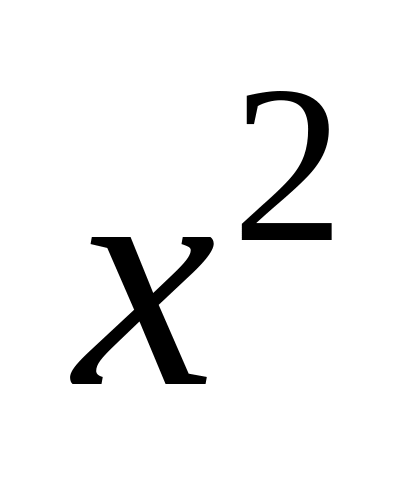
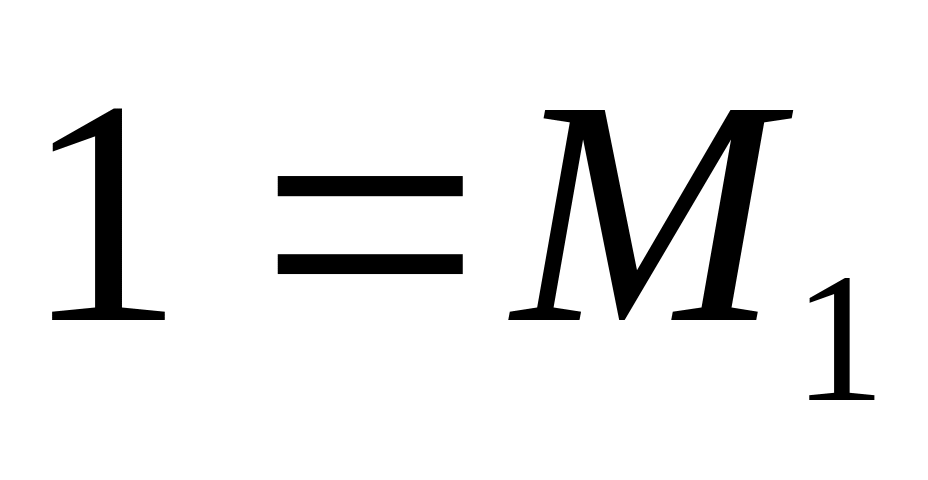
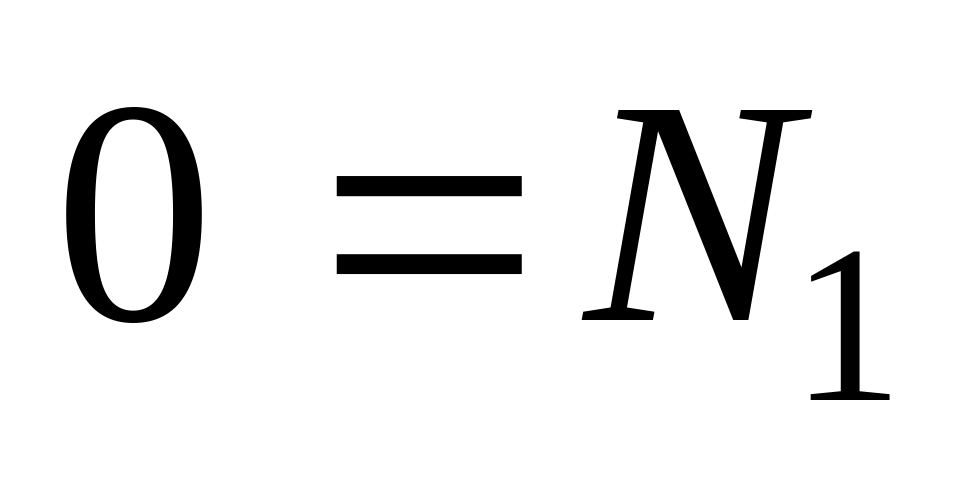
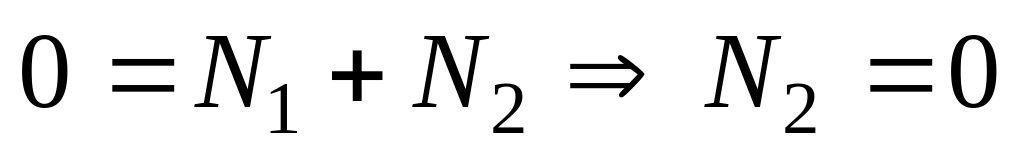
5. Следовательно, . ▼

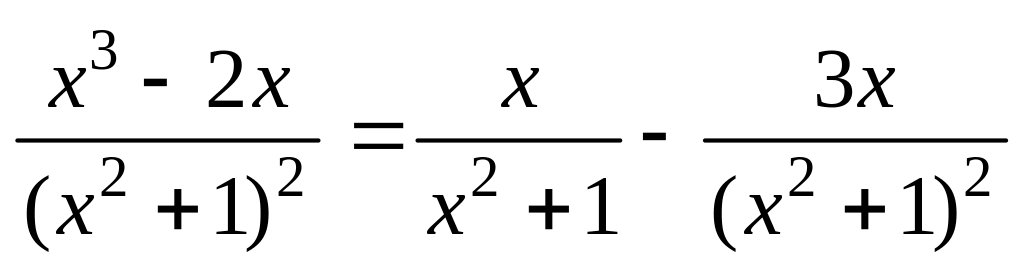Замечание - свободный член.

2. Интегрирование простейших дробей

Как было сказано выше, любую неправильную рациональную дробь можно представить в виде суммы некоторого многочлена и правильной рациональной дроби, причем это представление единственно.

Целая рациональная функция (многочлен) интегрируется непосредственно:

.

Так как любая правильная рациональная дробь представима в виде суммы простейших дробей, то ее интегрирование сводится к интегрированию простейших дробей. Рассмотрим вопрос об их интегрировании.

I. .

Задача IV.5. Найти интегралы: 1) ; 2) ; 3) ; 4) .

1) ▲ . ▼

2) ▲ . ▼

3) ▲ . ▼

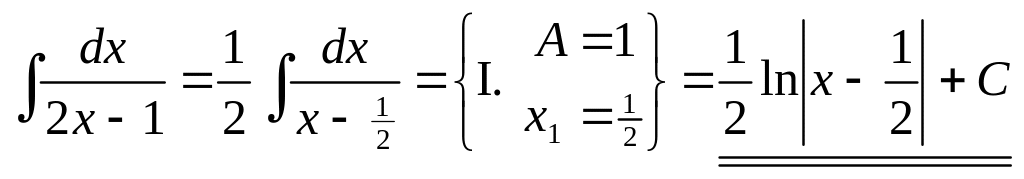4) ▲ . ▼

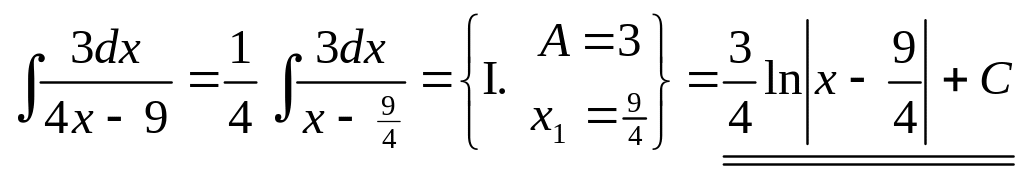II. .

Задача IV.6. Найти интегралы: 1) ; 2) ; 3) ; 4) .

1) ▲ . ▼

2) ▲ . ▼

3) ▲ . ▼

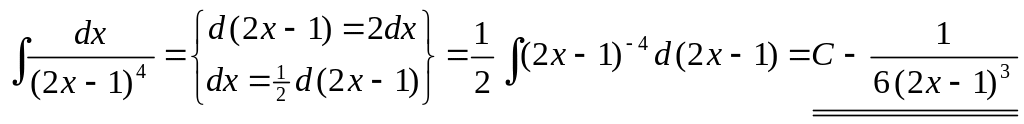4) ▲ . ▼

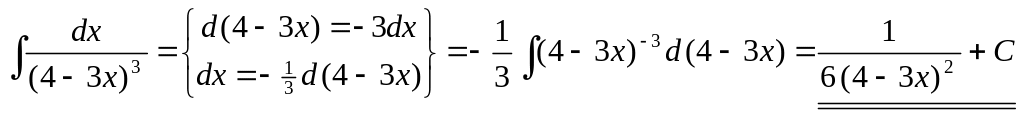Интегрирование дробей первых двух типов очевидно. Такие дроби дальше нужно интегрировать в уме.

III. .

1. Прием выделения полного квадрата из квадратного трехчлена.

.

Так как второе слагаемое , то положим его равным , где , а затем сделаем подстановку . Тогда, учитывая линейные свойства интеграла, найдем:

.

Замечание. Если в знаменателе дроби вместо квадратичного трехчлена находится трехчлен , то коэффициент следует вынести за скобку и тем самым свести этот случай к предыдущему.

Задача IV.7. Найти интегралы: 1) ; 2) ; 3) ; 4) .

1) ▲

. ▼

2) ▲

. ▼

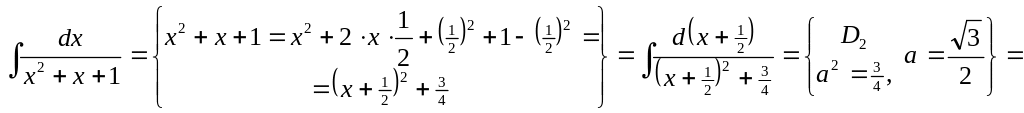
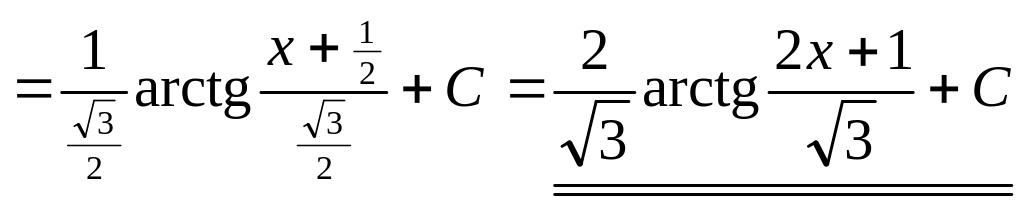3) ▲

. ▼

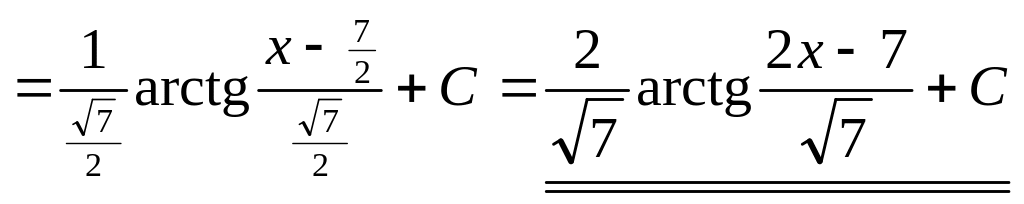4) Эта задача отличается от предыдущих задач тем, что коэффициент в знаменателе не равен единице. Для того чтобы свести этот случай к предыдущим, будем это коэффициент выносить за скобку.

▲

. ▼

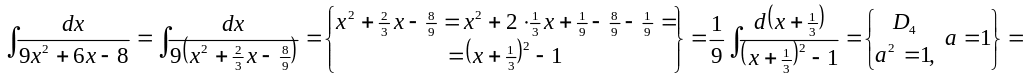
Задача IV.8. Найти интеграл

▲

. ▼

2. Прием выделения одной линейной функции из другой.

Для вычисления интеграла можно поступать так:

• в числителе подынтегральной дроби записывается производная знаменателя, т. е.

.

Тождественными преобразованиями получают заданный числитель .

Для этого следует двучлен умножить и к полученному произведению прибавить . Очевидно, что

.

• Преобразованная дробь имеет вид

и может быть представлена как сумма двух дробей:

.

Первая дробь интегрируется просто: в числителе находится производная знаменателя – интегрирование приводит к натуральному логарифму модуля знаменателя.

Для интегрирования второй дроби в знаменателе выделяют полный квадрат.

Задача IV.9. Найти интеграл .

▲

. ▼
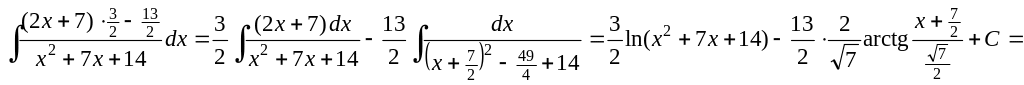