- •Учебно-методическое пособие для выполнения индивидуального задания неопределенный интеграл
- •Предисловие
- •Основные приемы и методы интегрирования Основная задача дифференцирования:
- •Основная задача интегрирования:
- •Основные свойства неопределенного интеграла
- •I. Непосредственное интегрирование
- •II. Интегрирование заменой переменной
- •Два способа замены переменной
- •Способ I.
- •Способ II.
- •Замена переменной в уме
- •Решение задач 1-14 типового варианта
- •III. Интегрирование по частям
- •Подынтегральное выражение представить в виде произведения двух сомножителей .
- •По установленному выражению надо дифференцированием найти .
- •По известному сомножителю определить интегрированием функцию .
- •Интегралы, для вычисления которых интегрирование по частям применяется несколько раз
- •Приведение интеграла к самому себе
- •1. Правило выбора частей:
- •Правило разложения правильной рациональной функции на простейшие
- •Корни знаменателя вещественные числа
- •Некоторые корни знаменателя кратные
- •Некоторые корни знаменателя – комплексные числа
- •Корни знаменателя – кратные комплексные числа
- •2. Интегрирование простейших дробей
- •Замечание. Под знаком логарифма трехчлен не взят по абсолютной величине, так как дискриминант отрицателен, а поэтому при любом значении этот трехчлен положителен.
- •3. Общий случай
- •Решение задач 19-21 типового варианта
- •V. Интегрирование выражений, содержащих тригонометрические функции
- •IV. Интегралы вида
- •V. Интегралы вида
- •1. Если подынтегральная функция имеет вид
- •2. Если подынтегральная функция имеет вид
- •Если функция не изменяется при замене на и
- •Решение задач 22-24, 26 типового варианта
- •VI. Интегрирование некоторых иррациональных функций
- •Рационализация подынтегральной функции
- •Подстановкой ,
- •Подстановкой ,
- •Если – целое число, то имеем рассмотренный выше случай интегрирования простейших иррациональных функций;
- •Если – целое число, то применяется подстановка , где – наименьшее общее кратное знаменателей дробей ;
- •Если – целое число, то используется подстановка , где – знаменатель дроби .
- •Решение задач 27, 28, 25 типового варианта
- •VI. Интегрирование разных функций
- •Еще раз напоминаем, что один и тот же интеграл можно найти по-разному
- •Знания и умения, которыми должен владеть студент
- •1. Знания на уровне понятий, определений, описаний, формулировок
- •2. Знания на уровне доказательств и выводов
- •3. Умения в решении задач Студент должен уметь:
- •Использованная литература
- •Содержание
- •Учебно-методическое пособие для выполнения индивидуального задания неопределенный интеграл
Основные свойства неопределенного интеграла
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
Линейность интеграла.
4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла
![]() .
.
5. Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме неопределенных интегралов от этих функций
![]() .
.
Следствие. Неопределенный интеграл от линейной комбинации конечного числа функций равен линейной комбинации неопределенных интегралов от этих функций
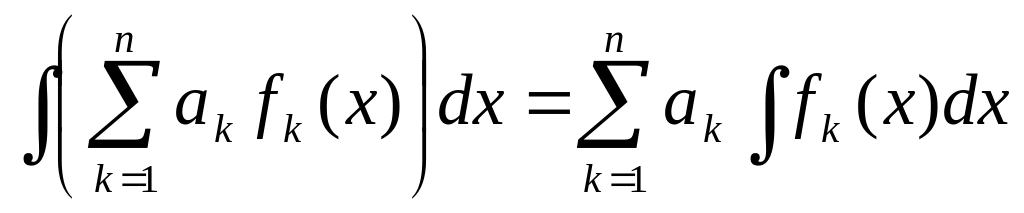 ,
,
где
![]() .
.
Вышеизложенные свойства позволяют сформулировать следующие два правила.
Для получения неопределенного интеграла от данной функции
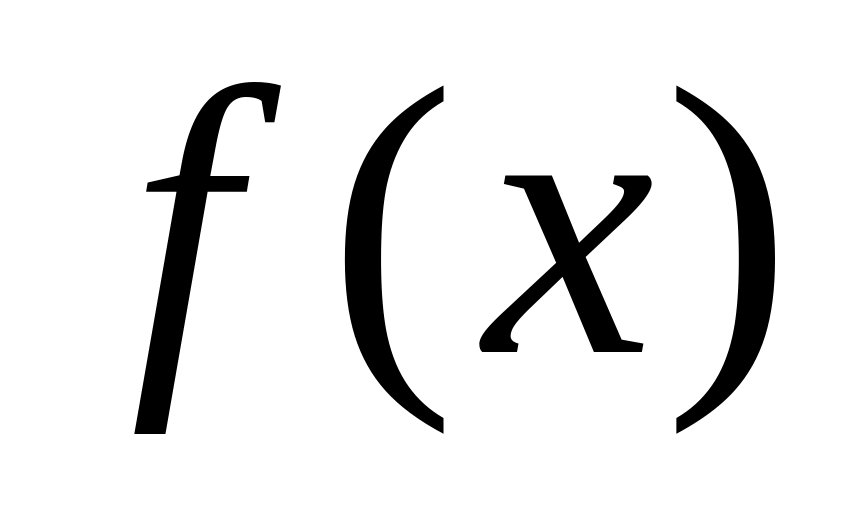 надо найти какую-либо первообразную
этой функции и прибавить к ней произвольную
постоянную.
надо найти какую-либо первообразную
этой функции и прибавить к ней произвольную
постоянную.Признаком правильности результата интегрирования является выполнение условия – производная от результата интегрирования должна быть равна подынтегральной функции
I. Непосредственное интегрирование
Будем рассматривать непосредственное интегрирование как совокупность простейших приемов интегрирования, владение которыми – необходимое условие умения интегрировать.
Таблица основных интегралов
Используя таблицу производных от простейших элементарных функций, мы можем составить таблицу некоторых простейших интегралов (в таблицу включены свойства). Все формулы из таблицы можно проверить путем дифференцирования согласно свойству 1, т. е. производная от правой части формулы всегда равна подынтегральной функции в левой части.
Правила интегрирования
![]() 1.
1.![]() .
.
2.
![]() .
.
3.![]() .
.
4.
![]() .
.
Интегралы, определяющие степенную, логарифмическую и показательную функции
![]() 1.
1.![]() .
.
2.![]() .
.
3.![]() .
.
4.
![]() .
.
Отметим
некоторые частные случаи формулы
![]() :
:
![]() (
(![]() означает интеграл с подынтегральной
функцией, тождественно равной единице);
означает интеграл с подынтегральной
функцией, тождественно равной единице);
![]() ;
;
![]() .
.
Упомянем еще и такую очевидную формулу:
![]() ,
,
![]() пишут вместо
пишут вместо
![]() и, вообще,
и, вообще,
![]() означает
означает![]() .
.
Интегралы, определяющие тригонометрические функции
![]() 1.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
Интегралы, определяющие обратные тригонометрические функции и логарифм сложного вида
![]() 1.
1.
![]() ,
,
![]() .
.
2.
![]() ,
,
![]() .
.
3.
![]() (для
знака « – » должно быть
(для
знака « – » должно быть
![]() ).
).
4.
![]() .
.
В
ссылках на таблицу будет указана буква,
соответствующая группе формул и номер
формулы в ней. Например,
![]() .
.


З
 АПОМНИТЬ
ТАБЛИЧНЫЕ ИНТЕГРАЛЫ
АПОМНИТЬ
ТАБЛИЧНЫЕ ИНТЕГРАЛЫ

 И
ПРОСТЕЙШИЕ ПРИЕМЫ
И
ПРОСТЕЙШИЕ ПРИЕМЫ
а) Непосредственное интегрирование по готовым формулам
Навыки интегрирования приобретаются опытом, а потому рекомендуется решить как можно больше задач.
Интегрирование
степенной функции (формула
![]() и ее частные случаи)
и ее частные случаи)
Задача
1.1. Найти интегралы: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() и самостоятельно проверить дифференцированием
полученные результаты.
и самостоятельно проверить дифференцированием
полученные результаты.
1)
▲
![]() .
▼
.
▼
2)
▲
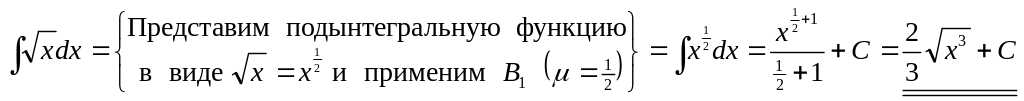 .
▼
.
▼
3)
▲
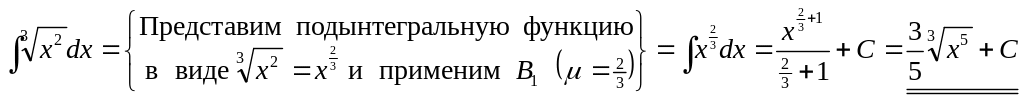 .
▼
.
▼
Проверка.
![]() .
.
4)
▲
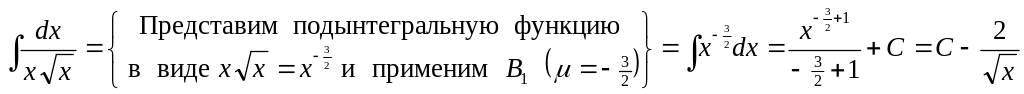 .
▼
.
▼
Задача
1.2. Найти интегралы: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() и самостоятельно проверить дифференцированием
полученные результаты.
и самостоятельно проверить дифференцированием
полученные результаты.
1)
▲
![]() . ▼
. ▼
2)
▲
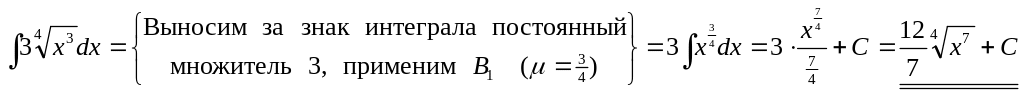 .
▼
.
▼
3)
▲
![]() .
▼
.
▼
Интегрирование
показательной функции (формула
![]() )
)
Задача
1.3. Найти
интегралы: 1)
![]() ;
2)
;
2)
![]() .
.
▲
![]() .
▼
.
▼
▲
![]() .
▼
.
▼
Применение формул
![]()
Задача
1.4. Найти интегралы: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
1)
▲
![]() .
▼
.
▼
2)
▲
![]() .▼
.▼
3)
▲
![]()
![]() .
▼
.
▼
4)
▲
![]()
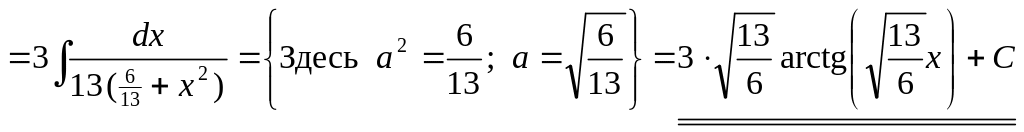 .
▼
.
▼
Задача
1.5. Найти интегралы: 1)
![]() ;
2)
;
2)
![]() .
.
▲
![]() .
▼
.
▼
▲
![]()
 .
▼
.
▼
Применение формул
![]()
Задача
1.6. Найти интегралы: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() .
.
1)
▲
![]() .
▼
.
▼
2)
▲
![]()
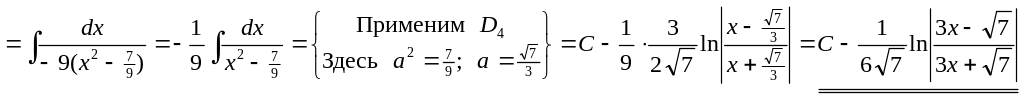 .
▼
.
▼
3)
▲
![]()
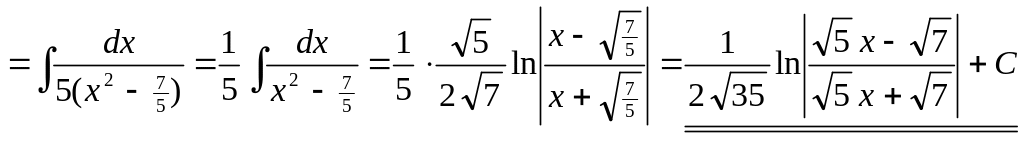 .
▼
.
▼
4)
▲
![]() .
▼
.
▼
5)
▲
![]()
![]() .
▼
.
▼
К АЖДЫЙ ДАННЫЙ ИНТЕГРАЛ СРАВНИВАЛИ
С ТАБЛИЧНЫМ,
« ПОДГОНЯЛИ» ЕГО К ОДНОМУ ИЗ ТАБЛИЧНЫХ
И ПОЛУЧАЛИ ОТВЕТ
б)
Интегрирование с использованием правил
![]() и алгебраических преобразований
и алгебраических преобразований
Задача
1.1. Найти интегралы: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ;
5)
;
5)
![]() .
.
1)
▲
![]()
![]() .
▼
.
▼
Замечание. При вычислении интеграла от суммы нескольких функций сумму произвольных постоянных, которая получается при этом, заменяют одной произвольной постоянной, обозначаемой обычно буквой .
2)
▲
![]()
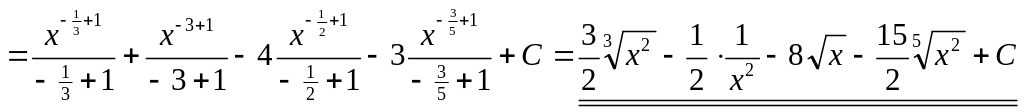 .
▼
.
▼
3)
▲

![]() .
▼
.
▼
4)
▲
![]()
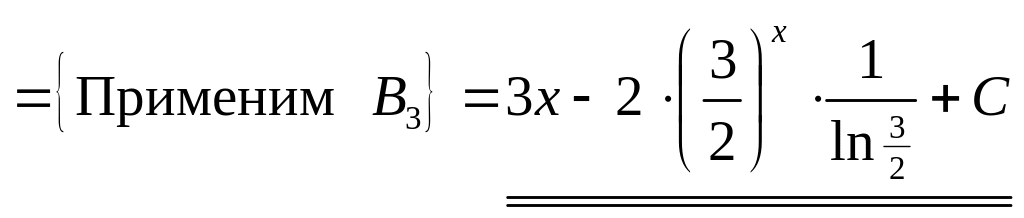 .
▼
.
▼
5)
▲
![]()
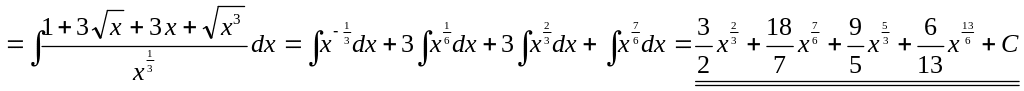 .
▼
.
▼
в) Использование простейших тригонометрических преобразований
Задача
1.1. Найти интегралы: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
1)
▲
![]()
![]() .
▼
.
▼
2)
▲
![]() .
▼
.
▼
3)
▲
![]()
![]() .
▼
.
▼
г) Независимость неопределенного интеграла от выбора аргумента функции
(использование правила
![]() )
)
При пользовании
формулами
![]() необходимо иметь в виду простейшие
преобразования дифференциала:
необходимо иметь в виду простейшие
преобразования дифференциала:
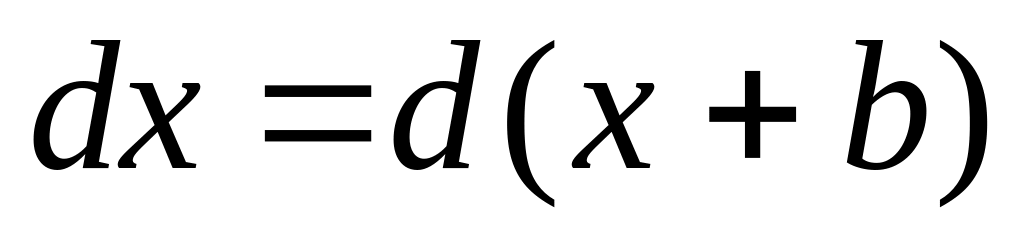 ,
где
,
где
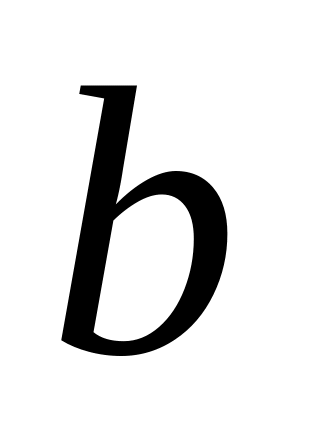 – постоянная.
– постоянная.
Под знак дифференциала можно прибавлять или вычитать постоянную величину.
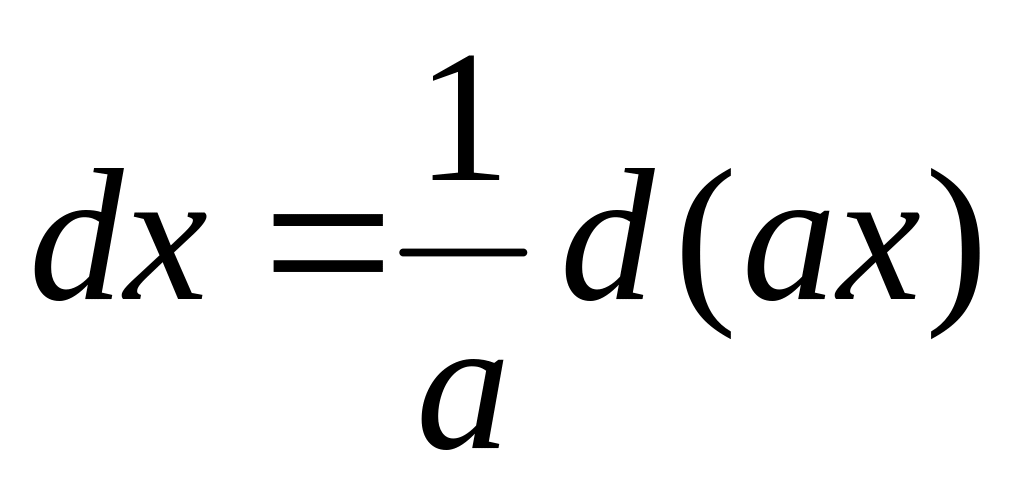 ,
где постоянная величина
,
где постоянная величина
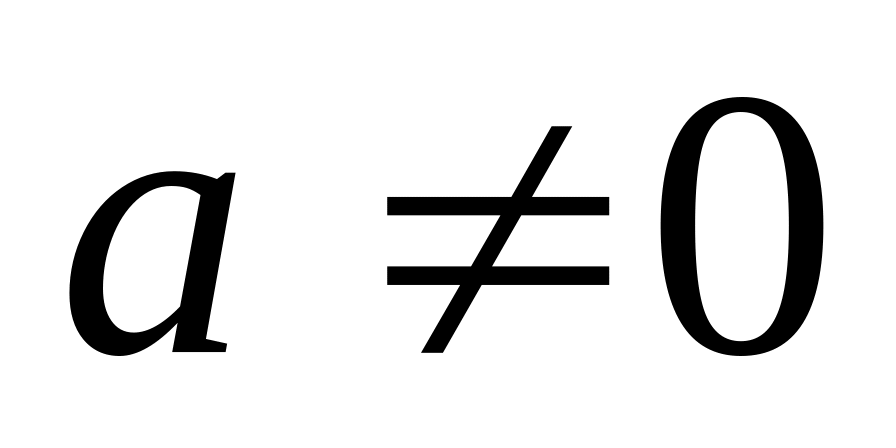 .
.
Прием "умножить – разделить".
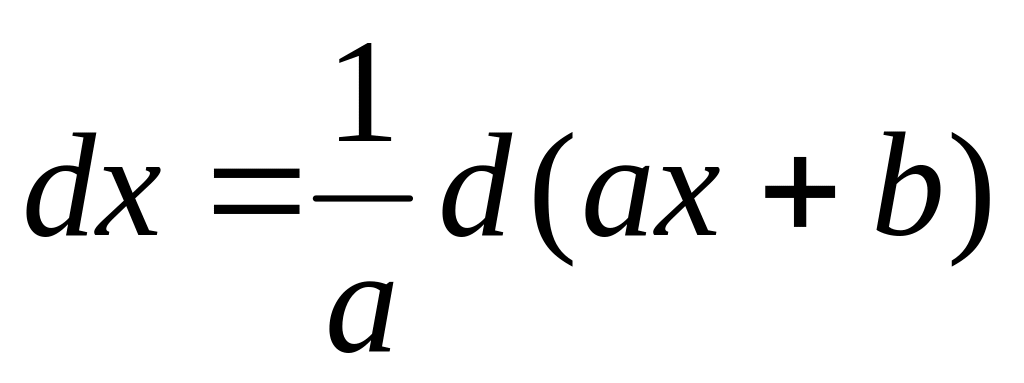 ,
где постоянная величина
.
,
где постоянная величина
.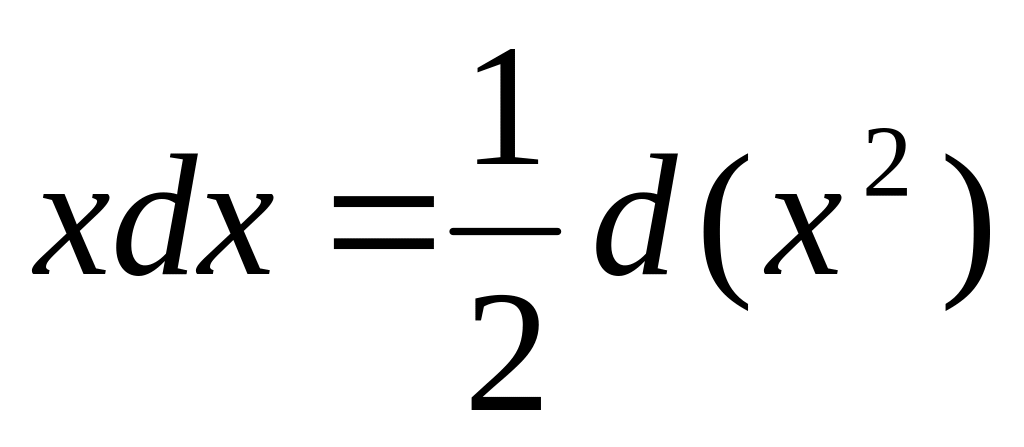 .
.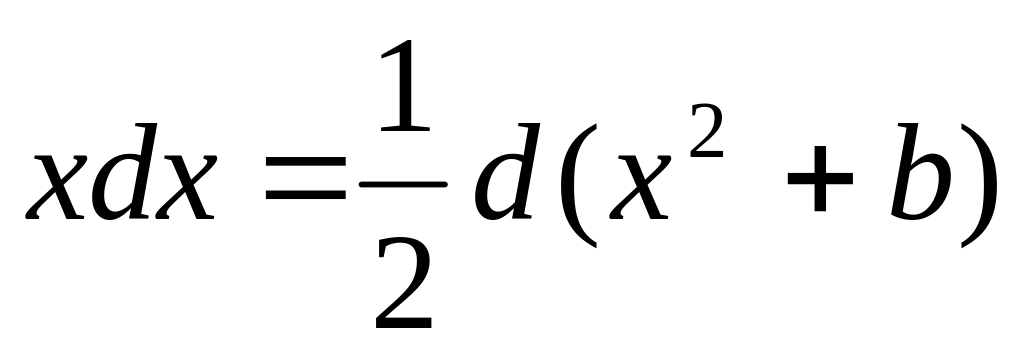 .
.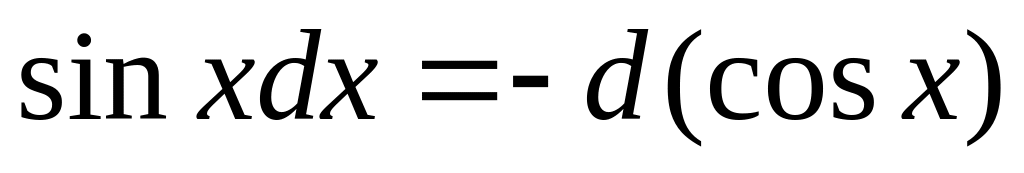 .
.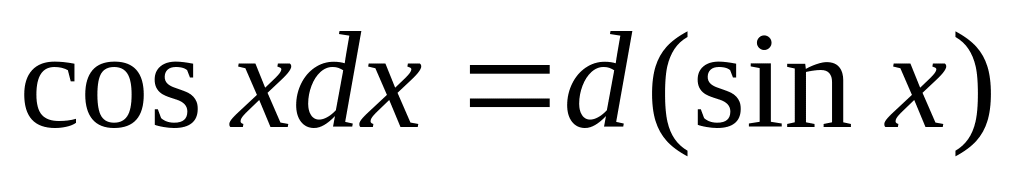 .
.
В общем случае
![]() .
.
Задача
1.1. Найти интеграл: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() .
.
1)
▲
![]()
![]() .
▼
.
▼
2)
▲
![]()
![]() .
▼
.
▼
3)
▲
![]()
![]() .
▼
.
▼
4)
▲
![]() .
▼
.
▼
5)
▲
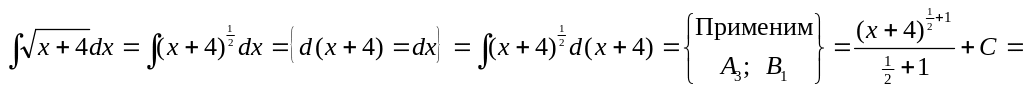
![]() .
▼
.
▼
6)
▲
![]() .
▼
.
▼
7)
▲
![]() .
▼
.
▼
Задача
1.2. Найти интегралы от тригонометрических
функций: 1)
![]() ;
2)
;
2)
![]() ;3)
;3)
![]() ;
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() .
.
Во всех интегралах
множители
![]() – величины постоянные, не равные нулю.
– величины постоянные, не равные нулю.
1)
▲
![]() .
.
Например,
![]() .
▼
.
▼
2)
▲
![]() .
.
Например,
![]()
![]() .
▼
.
▼
3)
▲
![]()
![]() .
.
Например,
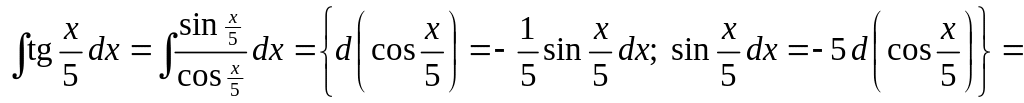
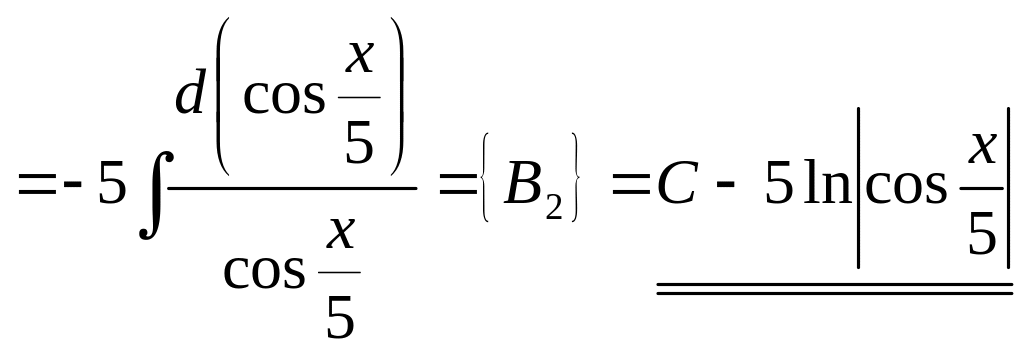 .
▼
.
▼
4)
▲
![]()
![]() .
.
Например,
![]()
![]() .
▼
.
▼
5)
▲
![]() .
.
Например,
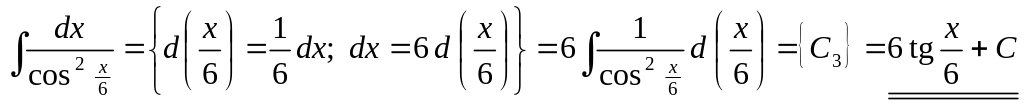 .
.
6)
▲
![]() .
.
Например,
![]() .
▼
.
▼
Задача
1.3. Найти интегралы: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() .
.
1)
▲
![]() .
▼
.
▼
2)
▲
![]() .
▼
.
▼
3)
▲
![]() .
▼
.
▼
4)
▲
![]()
![]() .
▼
.
▼
5)
▲
![]() .
▼
.
▼
6)
▲
![]() .
▼
.
▼
7)
▲
![]()
![]() .
▼
.
▼
Приведем еще несколько простейших приемов интегрирования, основанных на алгебраических преобразованиях подынтегральной функции.
д) Прием разложения подынтегральной функции
на сумму более простых для интегрирования функций
Задача
1.1. Найти интегралы: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
1)
▲
![]()
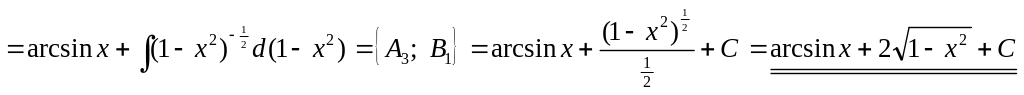 .
▼
.
▼
2)
▲
![]() .
▼
.
▼
3)
▲
![]()
![]() .
.
4)
▲
![]() .
▼
.
▼
е) Прием «прибавить – отнять»
Задача
1.1. Найти интегралы: 1)
![]() ;
2)
;
2)
![]() .
.
1)
▲
![]() .
▼
.
▼
2)
▲
![]()
![]() .
▼
.
▼
ОБЩАЯ СХЕМА НЕПОСРЕДСТВЕННОГO ИНТЕГРИРОВАНИЯ
|
Если
|
||
Н |
Сравните его с таблицей основных интегралов |
|
|
|
Если не совпадает, но похож на один из них, то нужно подобрать простейший прием; быстрее всех приводящий к табличному интегралу. |
||
Итак, Вы познакомились с простейшими приемами непосредственного интегрирования. Слово «простейшие» для Вас должно означать, что Вы, не задумываясь, сумеете применить любой из этих приемов. Большинство операций при применении простейших приемов следует выполнять в уме, только в этом случае Вы овладеете техникой интегрирования.


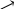

 айти
айти