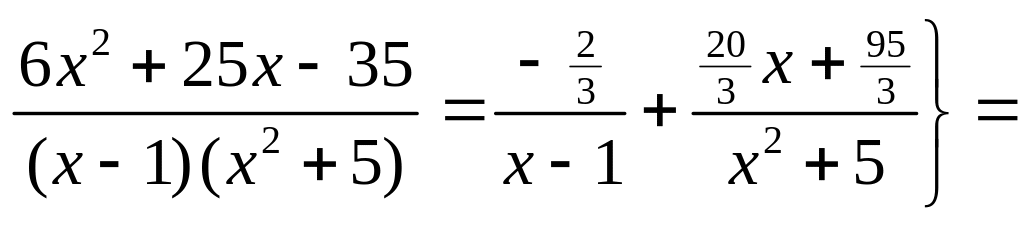Замечание. Под знаком логарифма трехчлен не взят по абсолютной величине, так как дискриминант отрицателен, а поэтому при любом значении этот трехчлен положителен.

IV. .

Для нахождения интеграла от простейшей дроби четвертого типа положим, как и выше,

.

Тогда получим

.

Обозначая интеграл в правой части , после преобразований имеем

.

Имеем так называемую рекуррентную формулу, которая позволяет найти интеграл для любого .

Задача IV.10. Найти интеграл .

▲ .

Полагая в рекуррентной формуле , будем иметь

,

и, следовательно, искомый интеграл равен

.

3. Общий случай

Для нахождения неопределенного интеграла от дробно-рациональной функции следует поступать следующим образом:

1. если рациональная дробь неправильная, то делением числителя на знаменатель выделяется целая часть, т. е данная функция представляется в виде суммы многочлена и правильной рациональной дроби;

2. знаменатель полученной правильной дроби разлагается на произведение линейных и квадратичных множителей;

3. написать схему разложения правильной дроби на сумму простейших дробей;

4. освободиться от знаменателей, умножая обе части равенства на знаменатель дроби;

5. найти неопределенные коэффициенты и подставить их в схему разложения (найти сумму простейших дробей);

6. используя линейность интеграла, находятся интегралы от каждого слагаемого в отдельности.

Задача IV.11. Найти интегралы: 1) ; 2) ; 3) ;

1) ▲

. ▼

2) ▲

;

. ▼

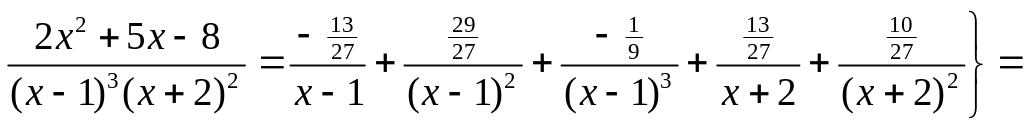
3) ▲

		; ;

. ▼

Решение задач 19-21 типового варианта

Найти неопределенные интегралы.

1. ▲

. ▼

2. ▲

. ▼

3. ▲

		;

.

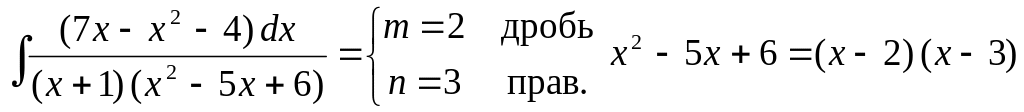
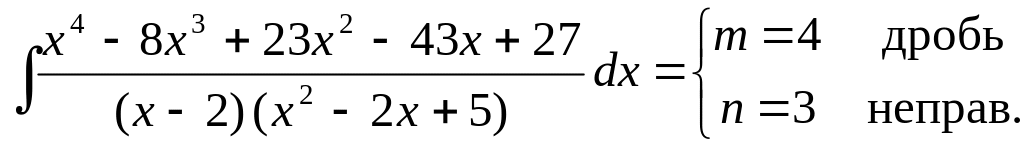
V. Интегрирование выражений, содержащих тригонометрические функции

I. Интегралы вида

,

где – целое положительное число.

Данные интегралы можно свести к формулам интегрирования, а, следовательно, и найти, руководствуясь следующими правилами:

1. Интегралы от нечетной степени синуса или косинуса можно найти

• путем отделения от нее одного множителя

• и замены кофункции новой переменной.

2. Интегралы от четной степени синуса или косинуса можно найти путем понижения степени (вдвое) по формулам:

.

Задача V.I. Найти интегралы: 1) ; 2) ; 3) .

1) ▲ Способ 1.

.

Способ 2.

. ▼

2) ▲ . ▼

3) ▲

. ▼

II. Интегралы вида

.

(Во всем дальнейшем – показатель степени синуса, – показатель степени косинуса).

Интегралы этого вида находят с помощью различных тригонометрических формул, применение которых зависит от показателей степеней . Рассмотрим наиболее часто встречающиеся случаи

1. Если хотя бы одно из чисел положительно и нечетно, то

• от нечетной степени отделяют множитель ,

• оставшийся множитель в четной степени преобразуют по формуле

,

• применяют подстановку .

2. Если оба показателя положительны и четны (или один из них – нуль), то показатели степени уменьшают с помощью формул:

.

3. Если целые отрицательные числа, то интеграл берется непосредственно, если в числителе единицу заменить 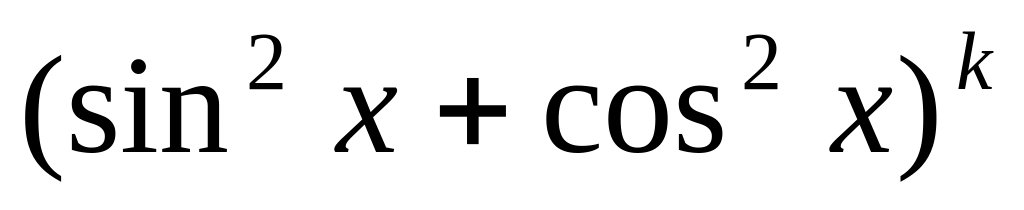, где – целая часть числа .

4. Если 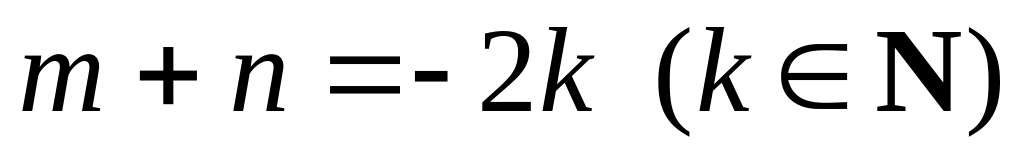, то подынтегральную функцию

• записывают (или она уже записана) в виде дроби,

• в знаменателе выделяют множитель (или ).

• Выражение заменяют ,

• применяют подстановку .

Задача V.II.1. Найти интегралы: 1) ; 2) ; 3) ; 4) .

1) ▲

. ▼

Замечание. Задачу можно решить, не вводя новую переменную (см. задачу V.I.1)). В дальнейшем поступаем именно так.

2) ▲

. ▼

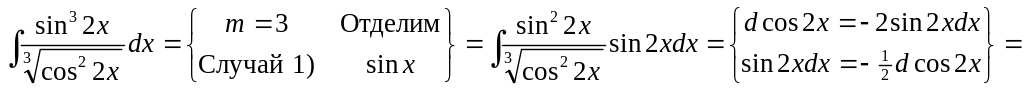
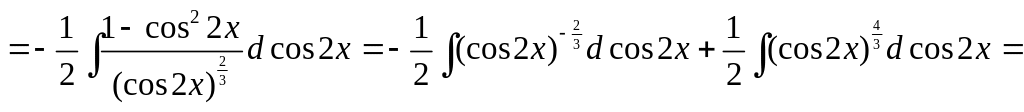
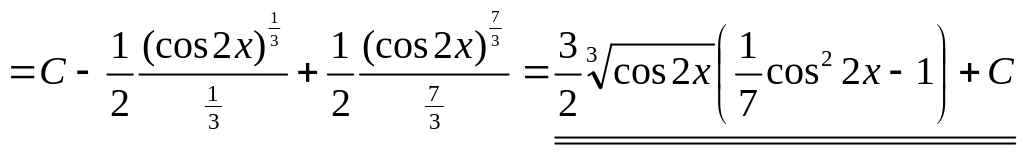3) ▲

. ▼

4) ▲

. ▼

Задача V.II.2. Найти интегралы: 1) ; 2) .

1) ▲

. ▼

2) ▲

. ▼

Задача V.II.3. Найти интеграл .

▲

. ▼

Задача V.II.4. Найти интегралы: 1) ; 2) .

1) ▲

. ▼

2) ▲

. ▼

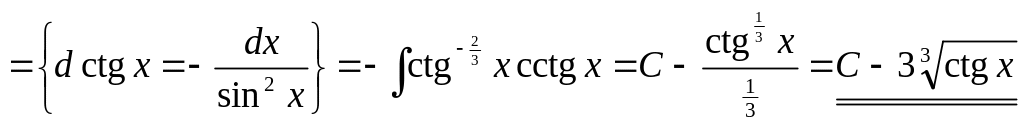III. Интегралы вида

,

где – целое положительное число.

1. К интегралу 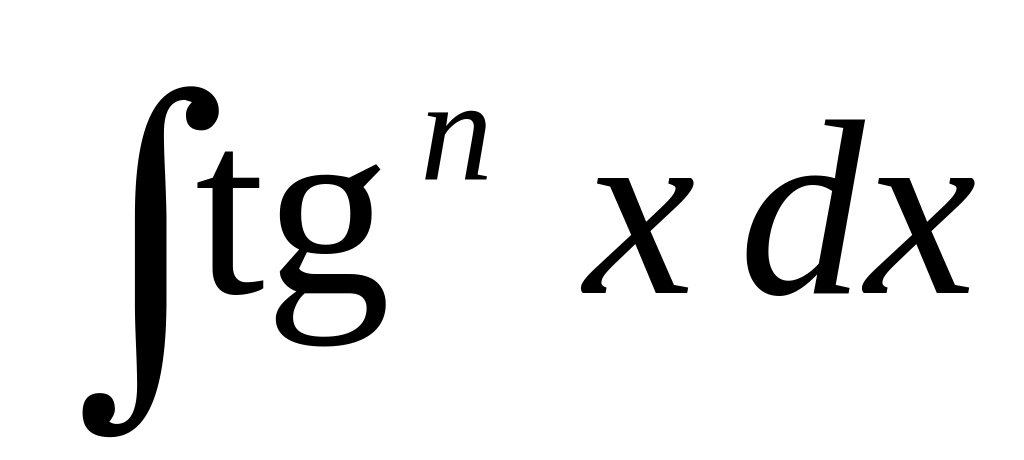следует применить подстановку .

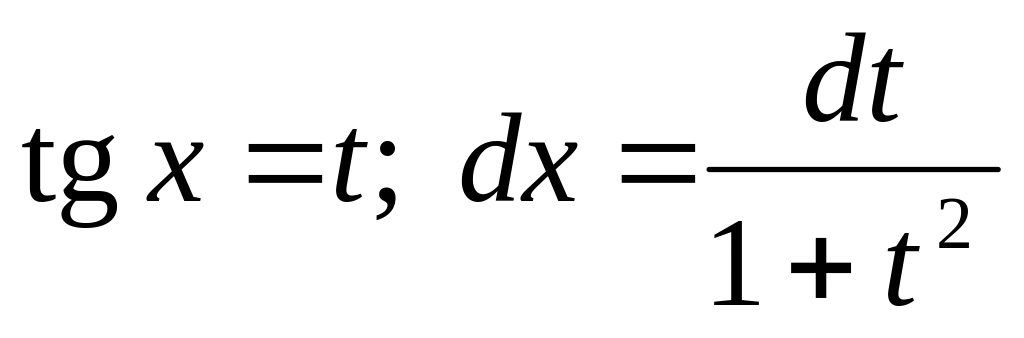Получим интеграл .

2) К интегралу удобно применить подстановку .

Получим интеграл .

3) Выполняя деление, придем к выражению, которое непосредственно интегрируется.

Задача V.III.1. Найти интегралы: 1) ; 2) .

1) ▲

. ▼

2) ▲

. ▼

Замечание. При нахождении интегралов применяется формула

,

с помощью которой последовательно понижается степень тангенса или котангенса.

Задача V.III.1. Найти интегралы: 1) ; 2) .

1) ▲

. ▼

2) ▲

.