Решение задач 1-14 типового варианта
Найти неопределенные интегралы (в задачах 1-5 результаты интегрирования проверить дифференцированием).
.
▲
.
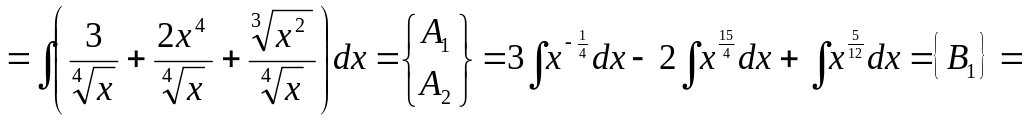
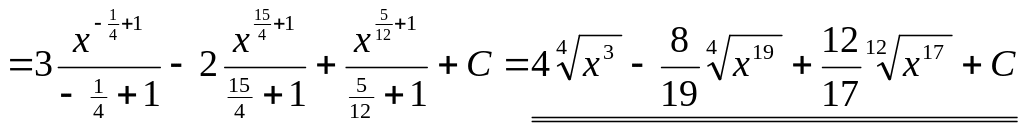Проверим полученный результат:
.
▼
.
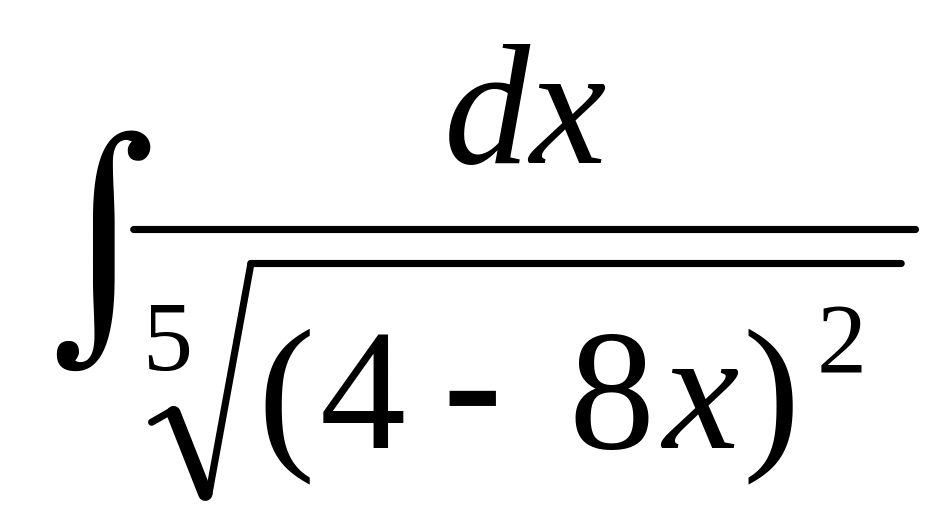▲ Способ 1.
.
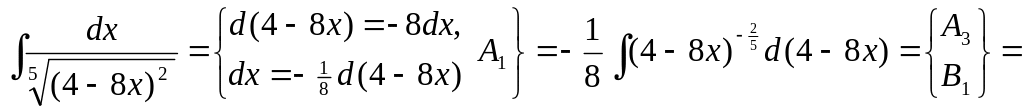
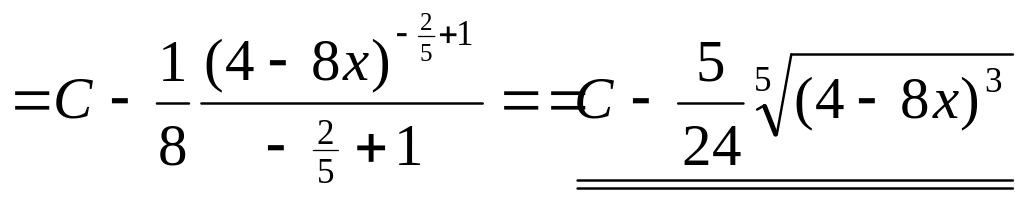▲ Способ 2.
.
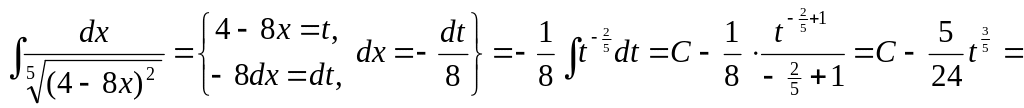
Проверим полученный результат:
.
▼
.
▲ Способ 1.
.
Способ 2.
.
Проверим полученный результат:
.
▼
.
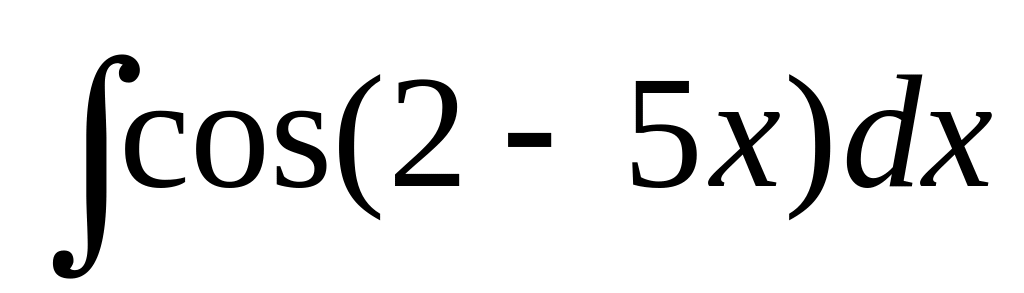▲ Способ 1.
.
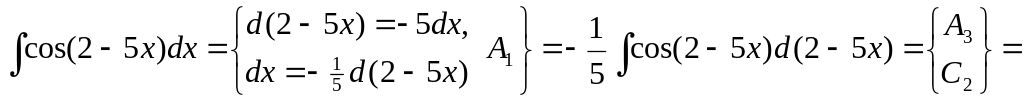
Способ 2.
.
Проверим полученный результат:
.
▼
.
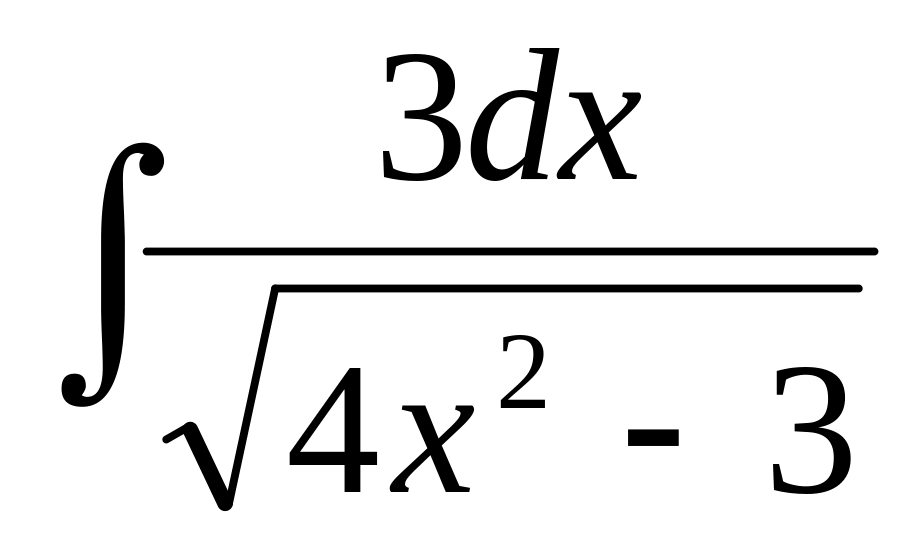▲ Способ 1.
.
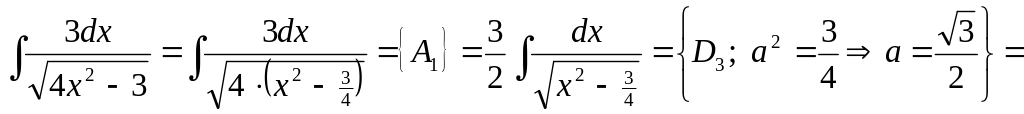
Способ 2.
.
Проверим полученный результат:
.
▼
.
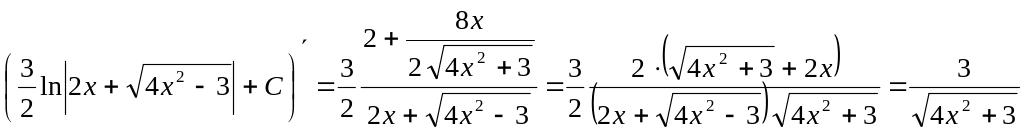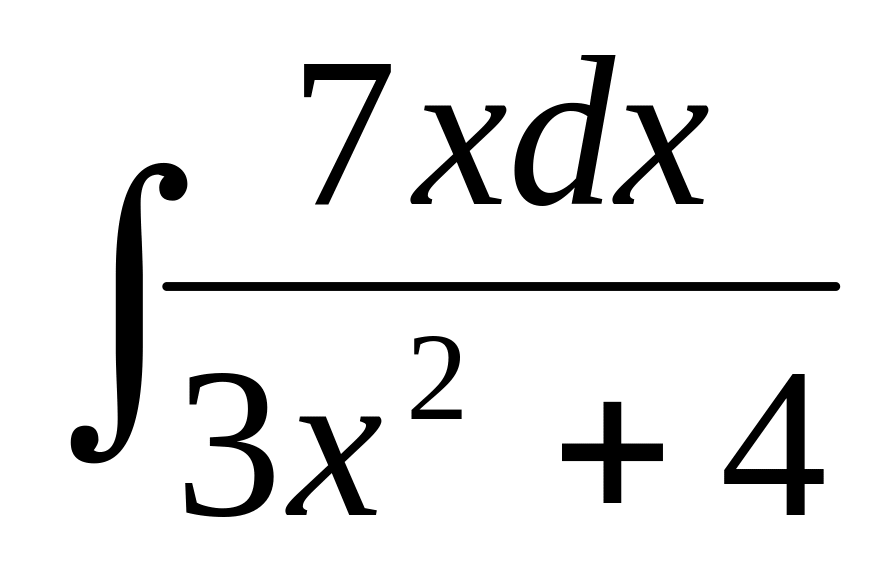▲ Способ 1.
.
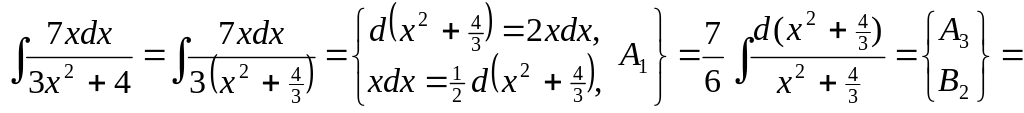
Способ 2.
.
▼
.
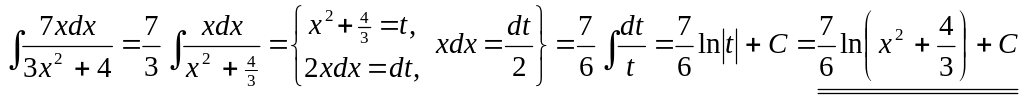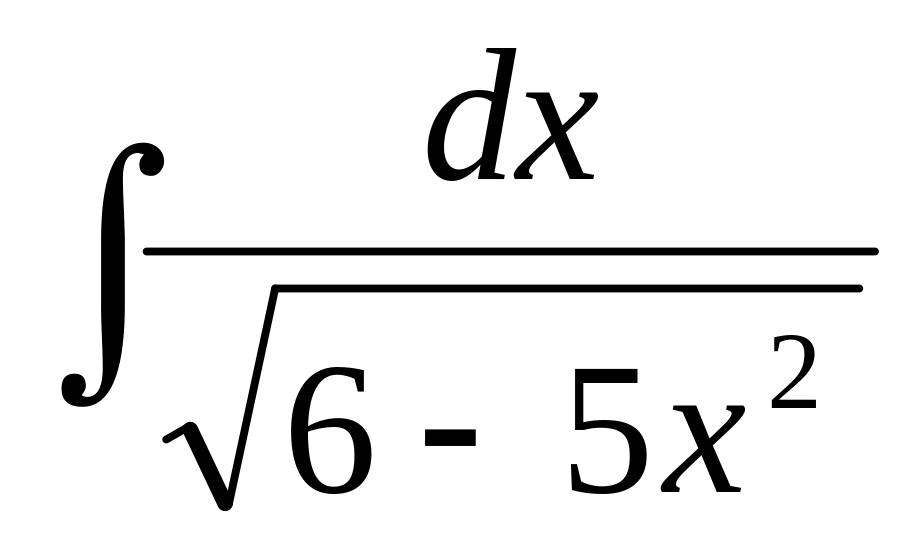▲ Способ 1.
.
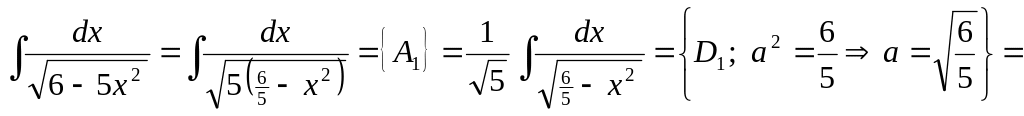
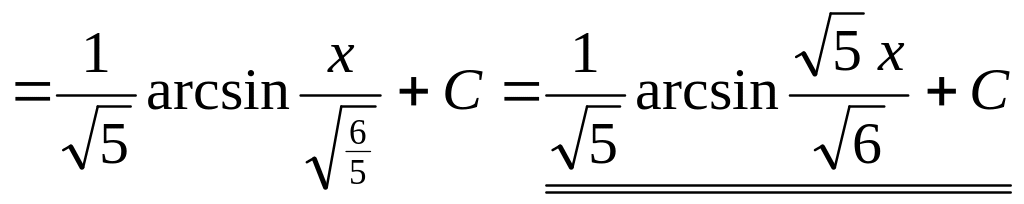Способ 2.
.
▼
.
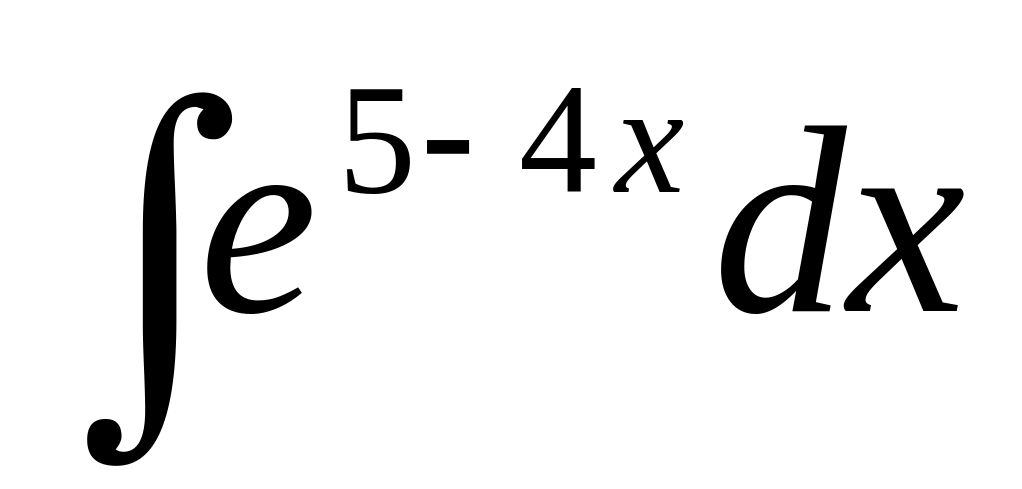▲ Способ 1.
.
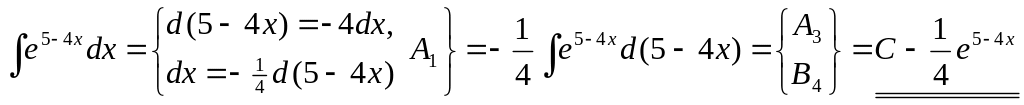Способ 2.
. 
.
▼
.
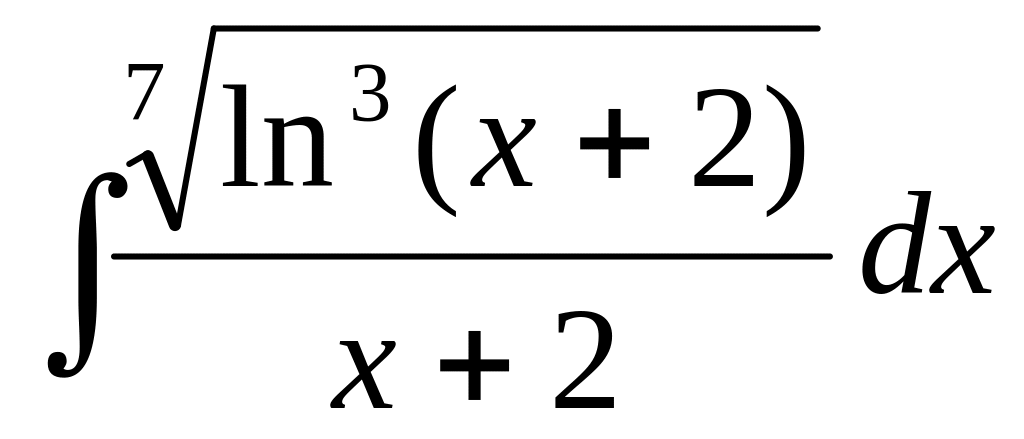▲ Способ 1.
.
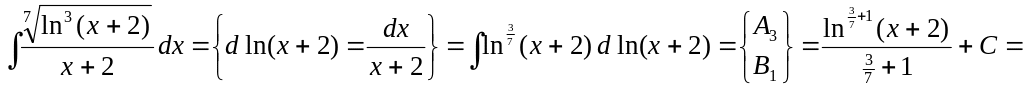
Способ 2.
.
▼
.
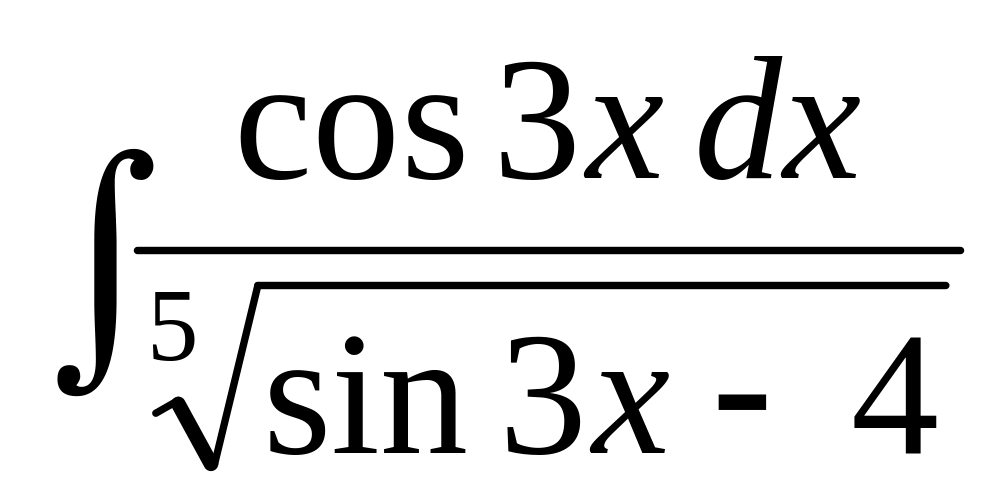▲ Способ 1.
.
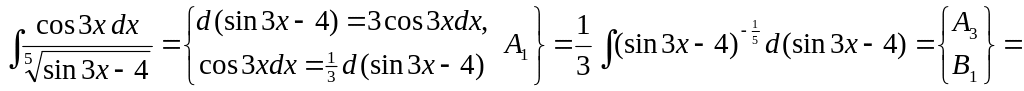
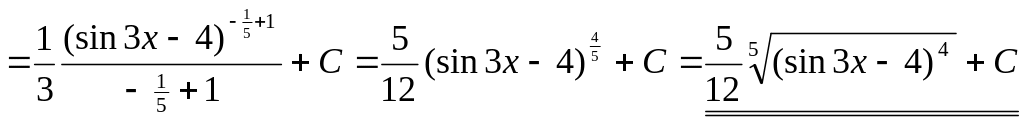Способ 2.
.
▼
.
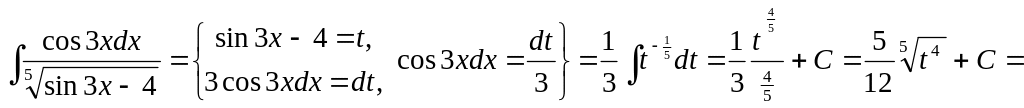
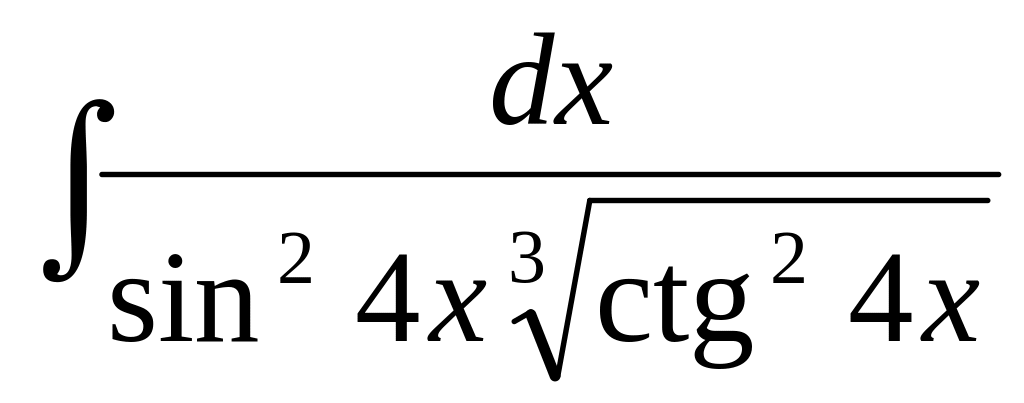▲ Способ 1.
.
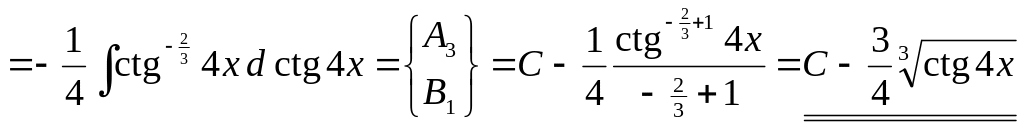Способ 2.
.
▼
.
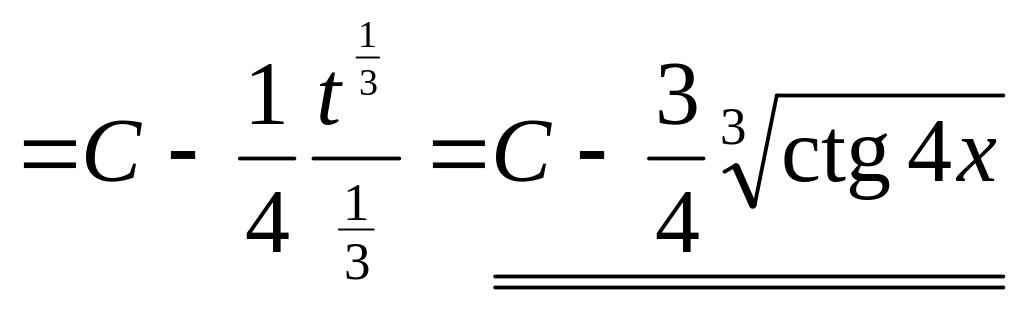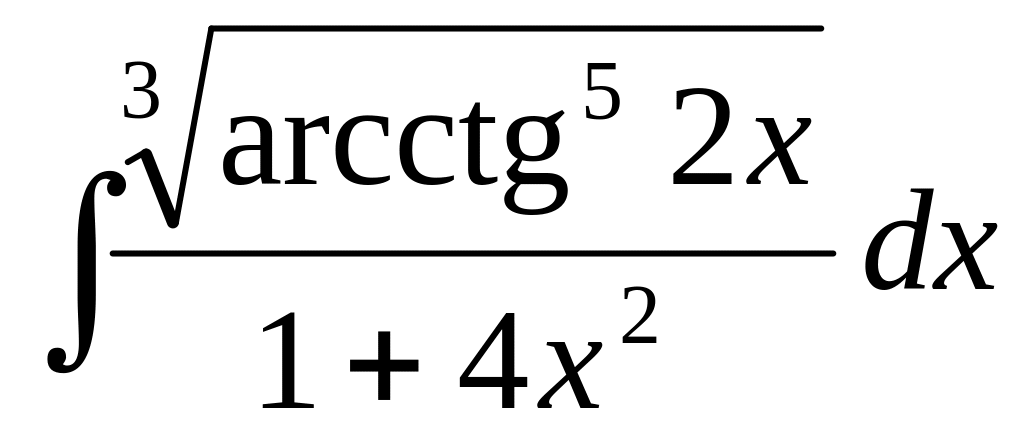Способ 1.
▲
.
Способ 2.
.
▼
.
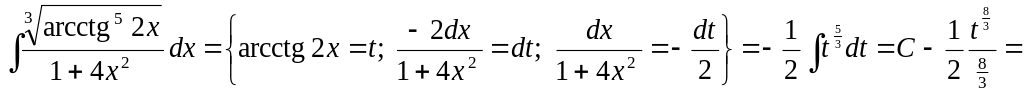
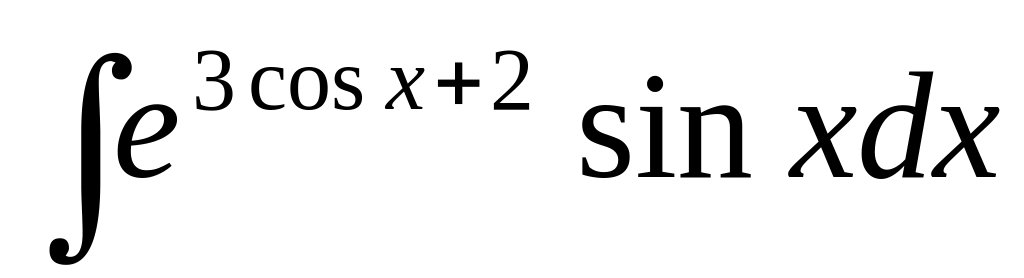Способ 1.
▲
.
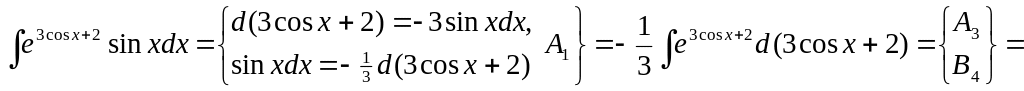
Способ 2.
.
▼
.
▲
.
▼
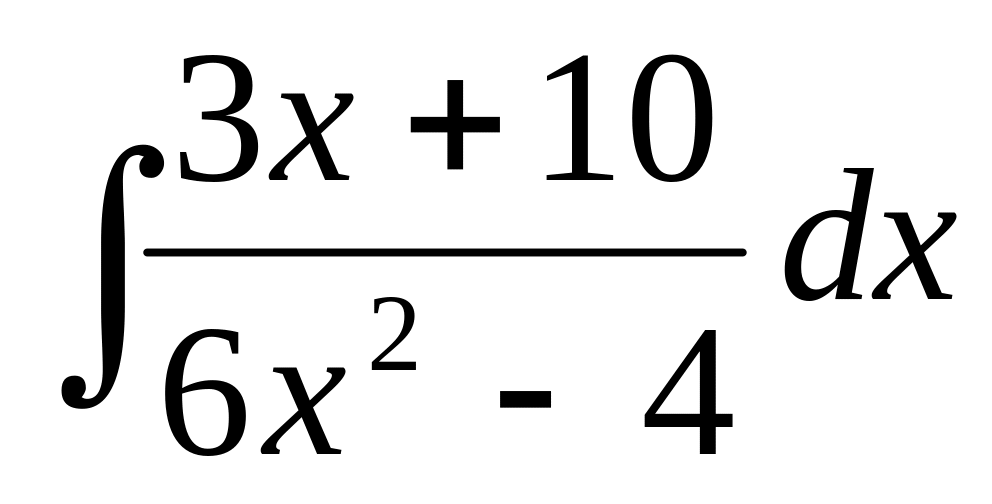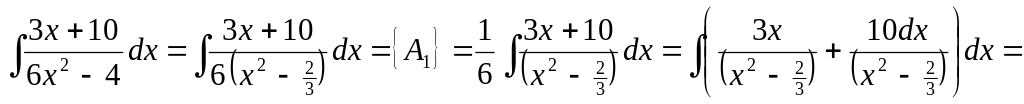
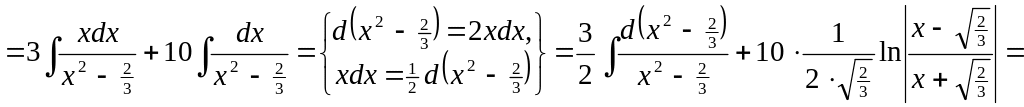
III. Интегрирование по частям
Интегрирование по частям основано на применении формулы
,
( III.1)
где
– непрерывно дифференцируемые на
некотором интервале функции. Формула
(III.1) называется формулой
интегрирования по частям. Она
дает возможность свести нахождение
интеграла
к отысканию интеграла
,
который во многих случаях оказывается
более простым.
Для применения формулы интегрирования по частям к некоторому интегралу следует:
Подынтегральное выражение представить в виде произведения двух сомножителей .
По установленному выражению надо дифференцированием найти .
По известному сомножителю определить интегрированием функцию .
Таким
образом, для применения формулы (III.1)
потребуется выполнить одно дифференцирование
для определения
и одно интегрирование для определения
.
За
всегда выбирается такое выражение,
содержащее
,
из которого посредством интегрирования
можно найти
;
в большинстве случаев принимается
функция, которая при дифференцировании
упрощается.
Полезно запомнить следующие 6 типов интегралов, вычислять которые удобно интегрированием по частям:
,
Здесь
– многочлен,
– постоянные множители.
Для
вычисления интегралов
полагаем:
;
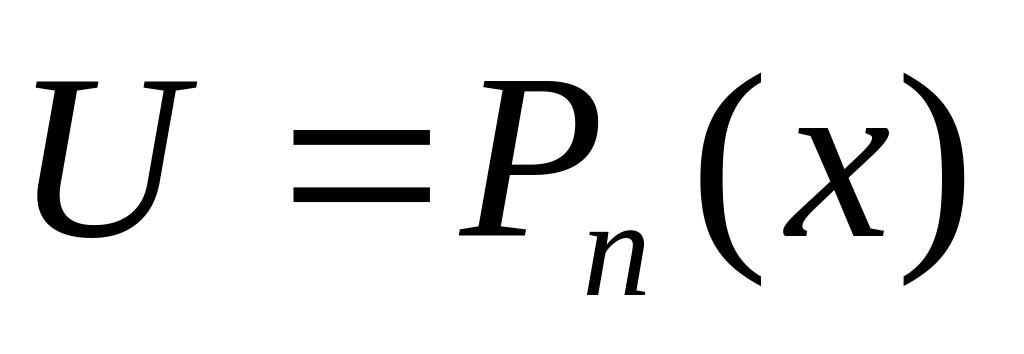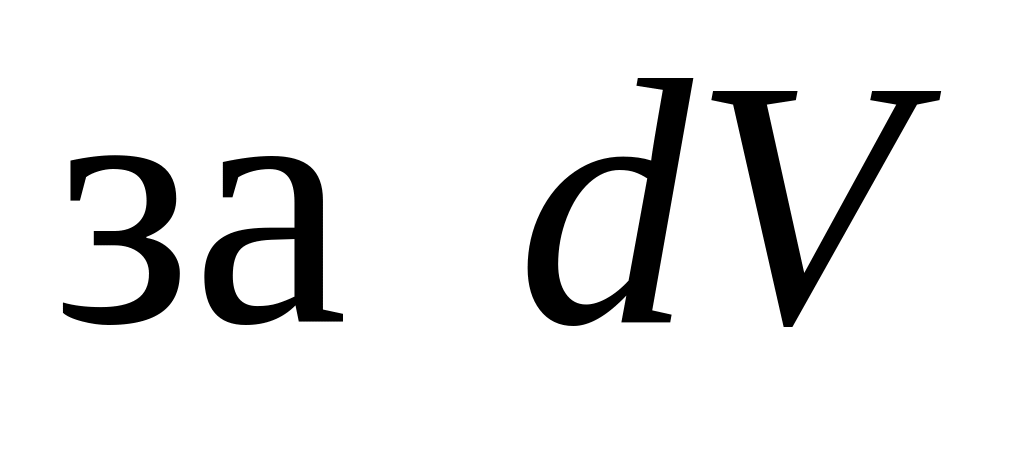принимается вся остальная часть
подынтегрального выражения.
Задача
III.1. Найти интегралы: 1)
;
2)
;
3)
.
1)
▲
.
▼
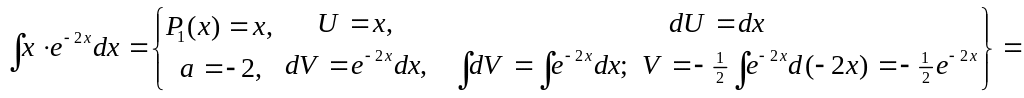
2)
▲
.
▼
3)
▲
.
▼
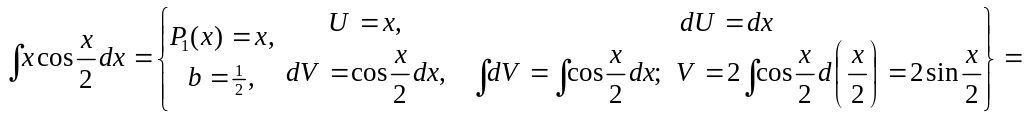
Для вычисления интегралов IV, V, VI:
следует принимать одну из функций
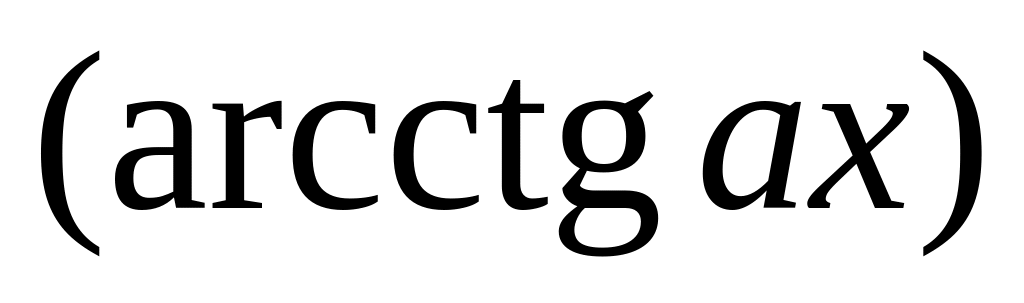;принимается вся остальная часть подынтегрального выражения.
Задача
III.2. Найти интегралы: 1)
;
2)
;
3)
;
4)
.
1)
▲
.
▼
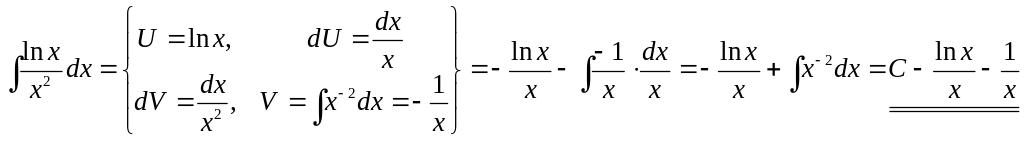2)
▲
.
▼
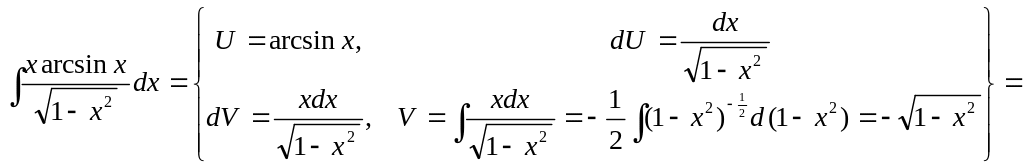
3)
▲
.
▼
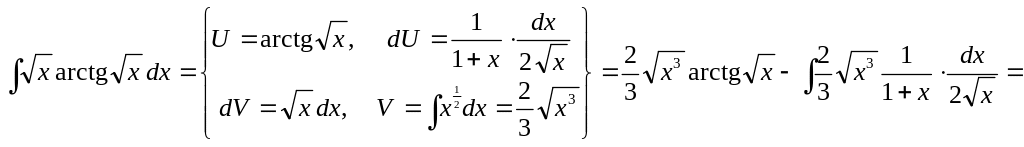
4)
▲
.
▼
Интегралы, для вычисления которых интегрирование по частям применяется несколько раз
Для вычисления интегралов I, II, III применяем формулу интегрирования по частям (III.1), полагая . Этот прием дает возможность постепенно понижать степень полинома, стоящего под знаком интеграла. Последовательно применяя формулу интегрирования по частям столько раз, какова степень многочлена , мы сведем вычисление данного интеграла к вычислению интеграла , где функция
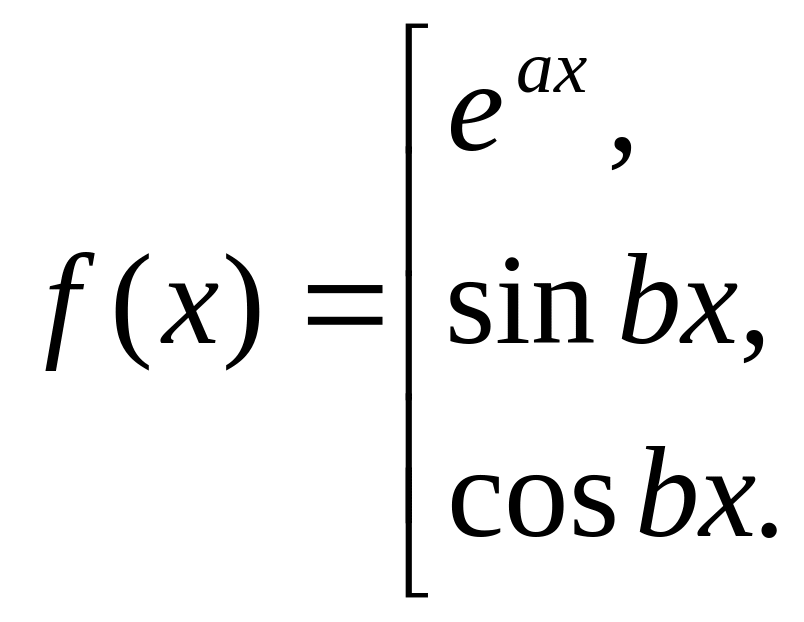
Задача
III. 3. Найти интегралы: 1)
;
2)
;
3)
;
4)
.
1)
▲
.
▼
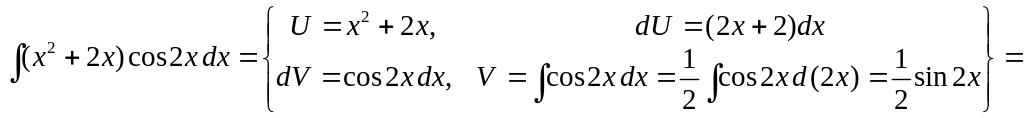
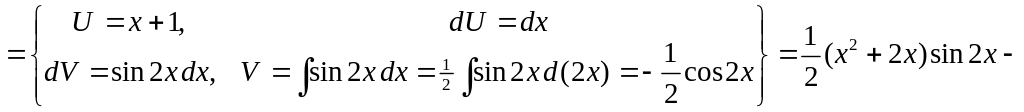
2)
▲
.
▼
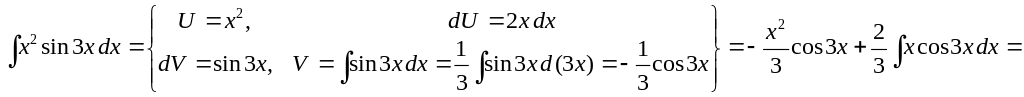
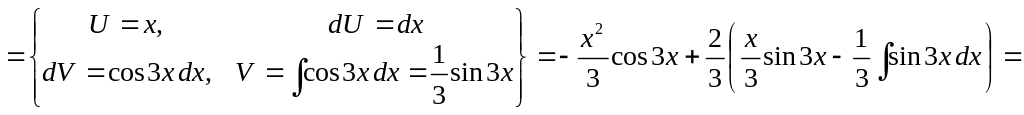
3)
▲
.
▼
4)
▲
.
▼
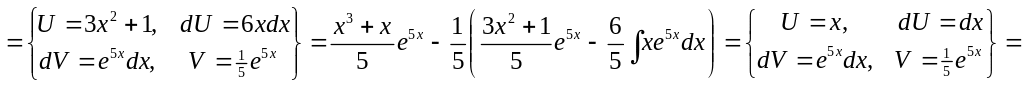
Аналогично,
интегралы IV, V, VI берутся по
частям столько раз, какова степень
подынтегральных функций
.
Задача
III. 4. Найти интегралы: 1)
;
2)
;
3)
.
1)
▲
.
▼
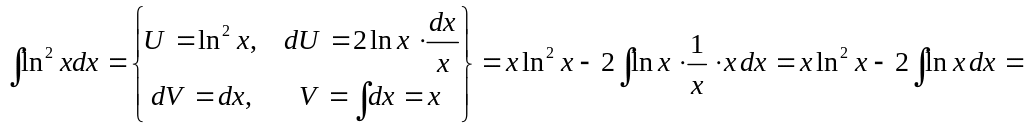
2)
▲
.
▼
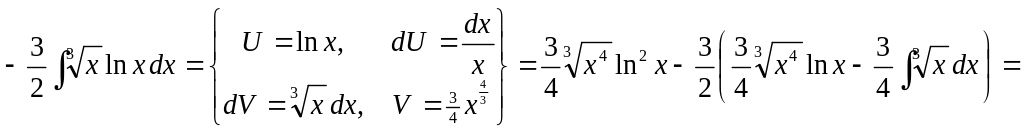
3)
▲
.
▼
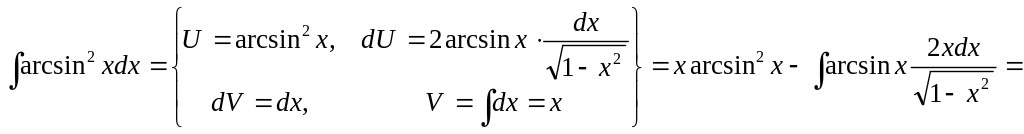
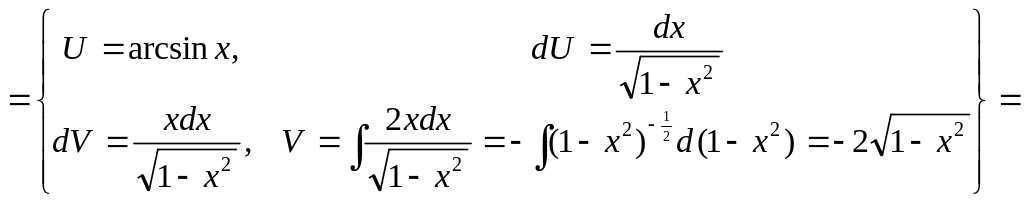