12. Расчет и оценка уравнения множественной регрессии средствами Excel

Построить модель множествен­ной линейной регрессии, которая позволит оценить объем товарооборота на ближайшую перспективу при заданных па­раметрах независимых переменных: «обо­рачиваемость товаров» и «удельный вес товаров с высо­кими торговыми надбавками». Исходные данные представлены в таблице 18.

Таблица 18 - Исходные данные

	А	В	С	D
1
2	Поряд­ковый номер месяца	Объем товаро­оборота, тыс. руб.	Обора­чивае­мость товаров, дни	Удельный вес товаров с высокими торговыми надбавками, %
3	1	28415	43,5	22,5
4	2	28231	43,0	18,0
5	3	29783	43,0	24,9
6	4	30969	43,5	24,4
7	5	30494	43,0	20,6
8	6	29757	42,5	19,0
9	7	30850	43,0	22,2
10	8	31325	41,5	21,6
11	9	31359	42,0	19,8
12	10	31610	41,5	19,7
13	11	32366	40,5	23,1
14	12	33313	40,0	23,9
15	13	33508	40,0	21,2
16	14	33374	39,0	20,4
17	15	34811	39,5	24,2
18	16	36046	39,0	26,5

Выполнение:

При построении модели множественной регрессии целесооб­разнее обратиться к инструменту Excel Регрессия, который предлагает исчерпывающую статистическую информацию о ее параметрах и качестве. Порядок работы с инструментом Регрессия определяется соответствующим окном диалога. Его можно вызвать через команду Анализ данных из контекстного меню панели Сер­вис. Диалоговое окно Регрессия предлагает пользователю определиться с набором следующих параметров (рис. 32).

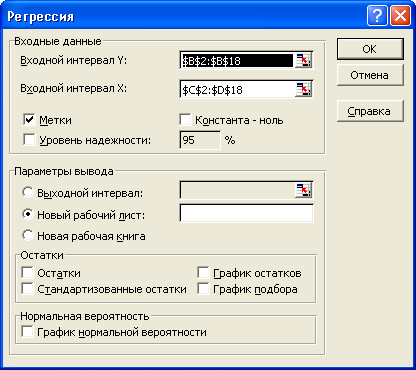
Рисунок 32 - Окно диалога «Регрессия»

Так, в первом разделе выходного массива «Регрессионная статистика» (см. ячейки А4:В8 табл. 19) приведены основные статистические характерис­тики общего качества уравнения: коэффициент множествен­ной корреляции R, коэффициент детерминации R², стандартная ошибка оценки. Значе­ние R², равное 0,892, свидетельствует о том, что на основе полученного уравнения регрессии можно объяснить 89,2 % вариации объема товарооборота.

Статистические характеристики второго раздела выход­ного массива «Дисперсионный анализ» (ячейки A10:F14) по­зволяют оценить меру разброса (дисперсию) зависимой пере­менной у и остаточной вариации (дисперсии) отклонений во­круг линии регрессии. Так, значение SS_р (ячейка С12) ха­рактеризует часть дисперсии, объясненную регрессией, а SS_о (ячейка С13) — часть дисперсии, не объясненной регрес­сией из-за наличия ошибок ε. При проведении регрессионно­го анализа особый интерес представляет изменение этих зна­чений по мере введения каждого регрессора. Качество моде­ли улучшится, если после введения в нее нового фактора зна­чение объясненной части дисперсии возрастет, а не объяс­ненной — снизится.

В ячейках D12:D13 отражены соответственно дисперсия исходного ряда (МS_p = SS_p / df, где df = k — см. ячейку В12) и несмещенная дисперсия остаточной компоненты (MS₀ = SS₀ / df, где df = п - k - 1 — см. ячейку В13).

В ячейке F12 второго раздела выходного массива приведен уровень значимости для оцененного F. Значения F-статистики (53,72) выглядит вполне допус­тимым, поскольку уровень значимости для нее (5,2•10⁷) ос­тается гораздо ниже 5%-ного предела, принятого для табличных F-статистик. Следова­тельно, есть основания ожидать, что F-наблюдаемое будет больше F_крит.

Оценив на основе первого и второго разделов выходного массива общее качество модели связи и убедившись в ее зна­чимости, можем перейти к третьему разделу (см. ячейки A16:G19 табл. 19), который содержит детальную информа­цию о параметрах уравнения регрессии. Приведенные в ячей­ках В17:В19 значения параметров (коэффициентов) уравне­ния позволяют придать формальный вид модели, построен­ной с помощью регрессионного анализа:

у = 71650,26 – 1098,94х₁ + 255,838х₂,

где х₁ — оборачиваемость товаров, дни; х₂ - удельный вес товаров с высокими торговыми надбавками, %.

Оценить значимость каждого параметра позволяют зна­чения t-статистики (см. ячейки D17:D19). Можно использо­вать приведенный в выходном массиве уровень значимости (см. ячейки Е17:Е19): если он не превышает 0,05 (т.е. 5%-ного уровня), то рассчитанные характеристики t-статистики будут больше табличного значения. Следовательно, статис­тическая значимость рассчитанных параметров уравнения весьма высока.

И, наконец, наряду с точечными значениями коэффици­ентов регрессии третий раздел выходного массива позволяет получить их интервальные оценки с доверительной вероят­ностью 95 % (см. ячейки F17:G19 табл. 19):

58598,85 < b < 84701,68; -1370,81 < m₁ < -827,08; 68,597 < m₂ < 443,079.

На основании изложенного можно с 95%-ной увереннос­тью утверждать, что параметры уравнения содержат информацию, значимую для расчета исследуемого показателя.

Таблица 19 - Регрессионный анализ

	А	В	С	D	E	F	G
1	ВЫВОД ИТОГОВ
2
3	Регрессионная статистика
4	Множественный R	0,94449
5	R-квадрат	0,892061
6	Нормированный R-квадрат	0,875455
7	Стандартная ошибка	767,1098
8	Наблюдения	16
9
10	Дисперсионный анализ
11		df	SS	MS	F	Значимость F
12	Регрессия	2	63223048,84	31611524,42	53,7193	5,2E-07
13	Остаток	13	7649947,599	588457,5077
14	Итого	15	70872996,44
15
16		Коэффициенты	Стандартная ошибка	t-статистика	P-значение	Нижние 95%	Верхние 95%
17	Y-пересечение	71650,26	6041,290874	11,86009163	2,41E-08	58598,85	84701,68
18	Оборачиваемость товаров, дни	-1098,94	125,8413656	-8,732770177	8,46E-07	-1370,81	-827,08
19	Удельный вес товаров с высокими торговыми надбавками, %	255,8378	86,67082253	2,951832613	0,011232	68,59687	443,0787