Теорія ймовірностей, ймовірнісні процеси і математична статистика

1. Класичне визначення ймовірності.

Эксперимент, исход которого невозможно предсказать, называют случайным экспериментом (СЭ).

Событие, которое в данном СЭ может произойти, а может и не произойти, называют случайным событием.

Элементарными исходами называют события, удовлетворяющие требованиям:

1. при всякой реализации СЭ происходит один и только один элементарный исход;

2. всякое событие есть некоторая комбинация, некоторый набор элементарных исходов.

Множество всех возможных элементарных исходов полностью описывает СЭ. Такое множество принято называть пространством элементарных исходов (ПЭИ). Выбор ПЭИ для описания данного СЭ неоднозначен и зависит от решаемой задачи.

Если элементарные исходы СЭ обладают свойством равновозможности (в силу определенной “симметрии” условий), то вероятность Р(А) любого события А определяется формулой:

Р(А) = n(A) / n ,

где n – общее число равновозможных исходов,

n(A) – число исходов, составляющих событие А, как говорят еще, благоприятствующих событию А.

2. Теореми додавання та множення ймовірностей.

Сумма событий А и В есть событие А+В, состоящее в наступлении хотя бы одного из событий А или В.

Произведение событий А и В есть событие А*В, состоящее в совместном наступлении обоих событий А и В.

События называются несовместными, если их совместное наступление невозможно.

П ротивоположное событие для события А есть событие А, состоящее в ненаступлении события А. События А и А – несовместны, а их сумма совпадает с ПЭИ.

Некоторые свойства:

Вероятность события А, вычисленная в предположении, что событие В произошло, называется условной вероятностью Р(А/В).

События А и В называются независимыми, если Р(А/В) = Р(А) (или Р(В/А) = Р(В)).

Теорема умножения 1.(ТУ1): Р(АВ) = Р(А)*Р(В/А) = Р(В)*Р(А/В).

ТУ 2.: вероятность совместного наступления независимых событий равна произведению их вероятностей.

Теорема сложения 1.(ТС1): вероятность суммы попарно несовместных событий равна сумме их вероятностей.

Т С 2.: Р(А) = 1 – Р(А).

ТС 3.: Р(А+В) = Р(А) + Р(В) – Р(АВ).

3. Формула повної ймовірності. Формула Байєса.

Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B1, B2, ..., Вn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Р (А) = Р (В1) P_B1 (А) + Р (В2) P_B2 (A) + ... + Р(Вn)Р_Bn(А).

Эту формулу называют «формулой полной вероятности».

Основные определения и формулы :

Пусть событие А может произойти только совместно с одним из попарно несовместных событий Н₁, Н₂, … , Н_n (это имеет место, например, для полной группы событий Н_к, к = 1.. n). Тогда:

Р(А) = Р(А/Н_к). (формула полной вероятности).

Если при этом Р(А)  0, то

Р(Н_m/А) = 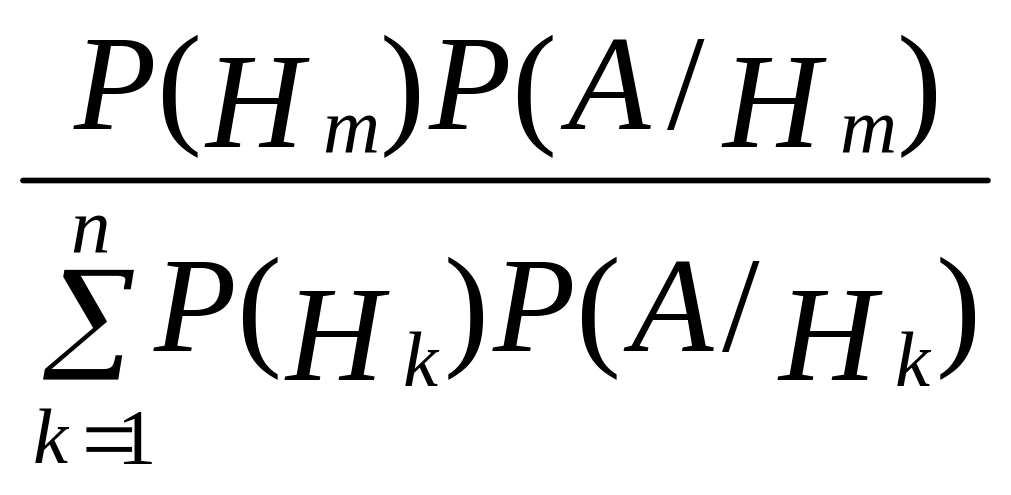, m = 1 .. n . (формула Байеса).

Выбор подходящих гипотез Н₁, Н₂, … , Н_n зависит от того, можем ли мы достаточно просто вычислить условные вероятности Р(А/Н_к).

4. Послідовності випробувань. Повторюванні експерименти. Схема Бернуллі. Локальна і інтегральна теореми Муавра-Лапласа. Поліноміальна схема.

Сформулируем основные формулы и определения, пусть осуществляется n независимых повторений некоторого эксперимента (или n независимых экспериментов), в каждом из которых может произойти событие А. Если вероятность этого события в каждом испытании равна р, то вероятность Р(n;k) того, что в n испытаниях событие А наступит ровно к раз определяется формулой Бернулли :Р(n;k) = .

В случае когда вероятность события А в m-ом испытании равна p_m , m = 1.. n, вероятность Р(n;k) равна коэффициенту при z^k в разложении производящей функции :

G(z) = 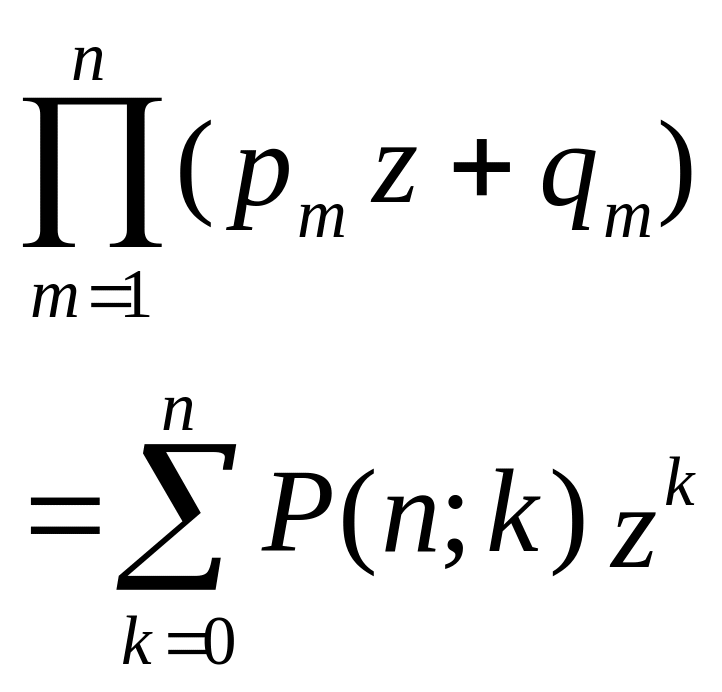, где q_m = 1 – р_m. Другое обобщение формулы Бернулли состоит в следующем. Пусть в каждом из независимых испытаний может появиться одно из m несовместных событий A_i и P(A_i) = p_i во всех испытаниях, =1. Тогда вероятность Р(n;k₁;k₂;…;k_m) того, что в n испытаниях событие A_i произойдет k_i раз, i = 1..m, , определяется полиномиальной формулой:

P(n;k₁;k₂;…;k_m) = 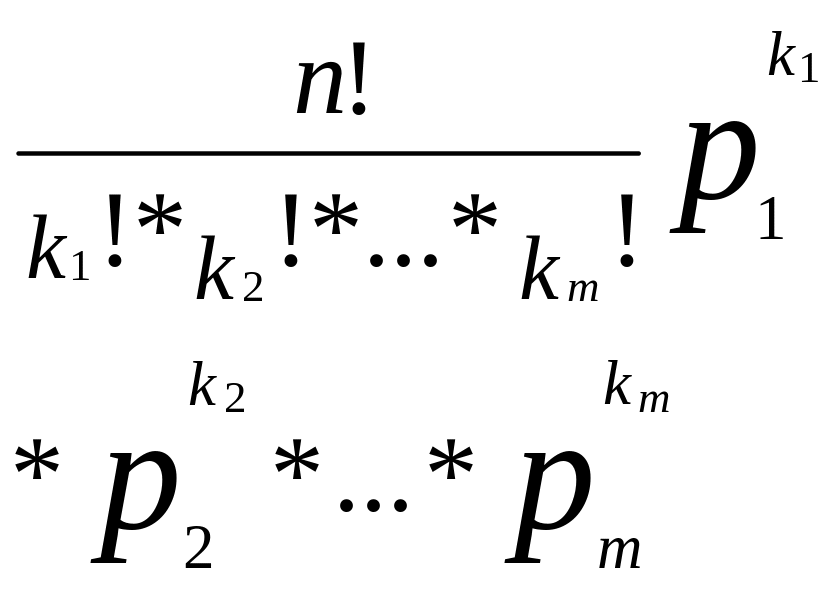.Наиболее вероятное число m₀ появлений события А в n испытаниях (если в каждом испытании Р(А) = р) равно целой части числа р(n+1). Если р(n+1) – целое, то наибольшее значение вероятности Р(n;k) достигается при двух числах: m₀ = р(n+1) и m₀ = 1.

Основные формулы и определения для большого N

Пусть в каждом из независимых испытаний событие А может произойти с вероятностью q, q = 1 – p. Обозначим как и раньше, через P(n;k) вероятность ровно к появлений события А в n испытаниях. кроме того, пусть P(n; k₁, k₂) – вероятность того, что число появлений события А находится между к₁и к₂.

Локальная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то

P(n;k) где - функция Гаусса.

Интегральная теорема Лапласа. Если n – велико, а р – отлично от 0 и 1, то

P(n; k₁, k₂) где - функция Лапласа.

Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций: а) (-х) = (х), (-х) = -(х); б) при больших х (х)  0, (х)  0,5.

Теоремы Лапласа дают удовлетворительное приближение при npq  9.

Теорема Пуассона. Если n – велико, а р – мало, то P(n;k) , где  = n*p.

Эта формула дает удовлетворительное приближение для р  0,1и np  10. При больших np рекомендуется применять формулы Лапласа.